11.8: Tresca Yield Condition

Last updated
Save as PDF

Page ID: 24885

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The stress state in uni-axial tension of a bar depends on the orientation of the plane on which the stresses are resolved. In Chapter 2 it was shown that the shear stress \(\tau\) on the plane inclined to the horizontal plane by the angle \(\alpha\) is

\[\tau = \frac{1}{2} \sigma_{11} \sin 2\alpha \]

where \(\sigma_{11}\) is the uniaxial tensile stress, see Figure (\(\PageIndex{1}\)).

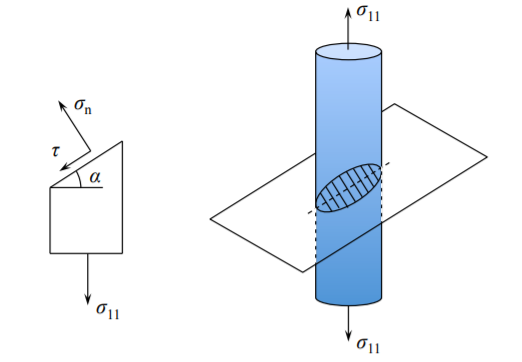
11.8.1.png — Figure \(\PageIndex{1}\): Shear and normal stresses at an arbitrary cut.

The maximum shear occurs when \(\sin 2\alpha = 1\) or \(\alpha = \frac{\pi}{4}\). Thus in uniaxial tension

\[\tau_{\text{max}} = \frac{\sigma_{11}}{2} \]

Extending the analysis to the 3-D case (see for example Fung) the maximum shear stresses on three shear planes are

\[\tau_1 = \frac{|\sigma_1 − \sigma_2|}{2}, \quad \tau_2 = \frac{|\sigma_2 − \sigma_1|}{2}, \quad \tau_3 = \frac{|\sigma_3 − \sigma_1|}{2} \]

where \(\sigma_1\), \(\sigma_2\), \(\sigma_3\) are principal stresses. In 1860 the French scientist and engineer Henri Tresca put up a hypothesis that yielding of the material occurs when the maximum shear stress reaches a critical value

\[\tau_o = \text{ max } \left\{ \frac{|\sigma_1 − \sigma_2|}{2}, \frac{|\sigma_2 − \sigma_3|}{2}, \frac{|\sigma_3 − \sigma_1|}{2} \right\} \]

The unknown constant can be calibrated from the uniaxial test for which Equation (11.4.9) holds. Therefore at yield \(\tau_o = \sigma_y/2\) and the Tresca yield condition takes the form

\[\text{ max } \{|\sigma_1 − \sigma_2|, |\sigma_2 − \sigma_3|, |\sigma_3 − \sigma_1|\} = \sigma_y \]

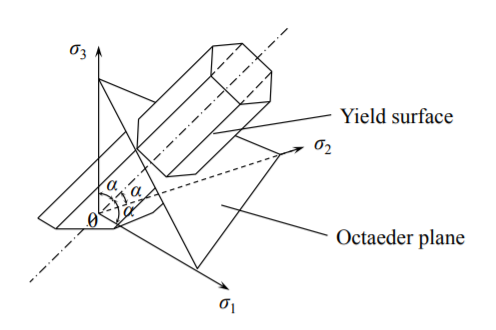
In the space of principal stresses the Tresca yield condition is represented by a prismatic open-ended tube, whose intersection with the octahedral plane is a regular hexagon, see Figure (\(\PageIndex{2}\)).

11.8.2.png — Figure \(\PageIndex{2}\): Representation of the Tresca yield condition in the space of principal stresses.

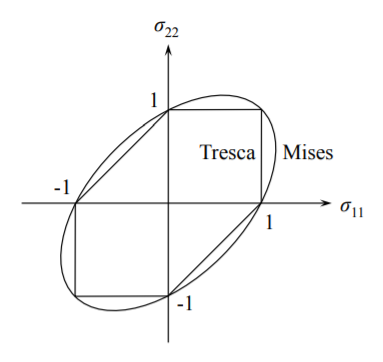
For plane stress, the intersection of the prismatic tube with the plane \(\sigma_3 = 0\) forms a familiar Tresca hexagon, shown in Figure (\(\PageIndex{3}\)).

11.8.3.png — Figure \(\PageIndex{3}\): Tresca hexagon inscribed into the von Mises ellipse.

The effect of the hydrostatic pressure on yielding can be easily assessed by considering \(\sigma_1 = \sigma_2 = \sigma_3 = p\). Then

\[\sigma_1 − \sigma_2 = 0 \]

\[\sigma_2 − \sigma_3 = 0 \]

\[\sigma_3 − \sigma_1 = 0 \]

Under this stress state both von Mises yield criterion (Equation (??)) and the Tresca criterion (Equation (??)) predict that there will be no yielding.