As already noted, charge is an attractive force. It is denoted by the letter \(Q\) and has units of coulombs. Electrons are negatively charged and protons are positively charged. All electrons and protons exhibit the same magnitude of charge, roughly 1.602E−19 coulombs. Thus, one coulomb is equivalent to the charge exhibited by approximately 1/1.602E−19, or 6.242E18 electrons. Further, opposite charges attract while like charges repel, similar to the poles of a magnet.
It is possible to move charge from one point to another. The rate of charge movement over time is called current. It is denoted by the letter \(I\) and has units of amps (or amperes)1. One amp of current is defined as one coulomb per second.
\[1 \text{ amp } \equiv 1 \text{ coulomb } / 1 \text{ second } \label{2.1} \]
That is, one amp can be visualized as approximately 6.242E18 electrons passing through a wire in a period of one second. Consider Figure 2.3.1
.
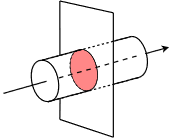
Figure 2.3.1
: Defining current as charge flow through a wire.
Here we have a wire with electrons flowing through it in the direction of the arrow. We cut this wire with an imaginary plane, leaving us with the highlighted disk. Now imagine that we could count the number of electrons passing through this disk over the course of one second. Because we know the charge possessed by one electron, we simply multiply the number of electrons by the charge for each to yield the total charge, and thus we arrive at the current. As a formula:
\[I = Q / t \label{2.2} \]
where
- \(I\) is the current in amps,
- \(Q\) is the the charge in coulombs,
- \(t\) is the time in seconds.
A common analogy for electric current is the flow of water through a pipe or river. Just as we can imagine water flow as “gallons or liters per minute”, we imagine electric current as “coulombs per second”.
In the course of one-half second, a certain battery delivers a charge of three coulombs. Determine the resulting current.
Solution
\[I = \frac{Q}{t} \nonumber \]
\[I = \frac{3C}{0.5s} \nonumber \]
\[I = 6 A \nonumber \]
A device delivers a current of 25 mA. Determine the charge transferred in two seconds along with the equivalent total number of electrons.
Solution
\[I = \frac{Q}{t} \nonumber \]
\[Q = I \times t \nonumber \]
\[Q = 25 mA \times 2s \; \text{ from Definition \ref{2.1}, amp-seconds is coulombs} \nonumber \]
\[Q = 50 mC \nonumber \]
As one coulomb is equivalent to 6.242E18 electrons, just multiply to find the total number of electrons transferred.
\[\text{Total electrons } = Q \times \text{ number of electrons per coulomb } \nonumber \]
\[\text{Total electrons } = 50 mC \times 6.242E18 \nonumber \]
\[\text{Total electrons } = 3.121E17 \text{ electrons} \nonumber \]
In sum, the larger the charge transferred within a given time period, the greater the current. Modern electrical and electronic systems might deal with currents of under a picoamp or, at the other extreme, thousands of amps. That is an astonishing range. It is roughly equivalent to a single drop of water dripping from a leaky faucet each second compared to 1000 times the flow of water over Niagara Falls.
References
1\(I\) stands for \(I\)ntensity (of current), and was so named by André-Marie Ampère.



