7.5: Concise Summary

An Entity Relationship (ER) model is a diagram that gives a good overview of the design of a database system with the aim of making it easier to be understood at a technical level. This model can be mapped to a relational schema which shows the relationship between its members. An ER diagram consists of multiple components: the entity, entity type, entity set, and attributes. 

The entity of the ER diagram is an object or concept about which you want to store information. This component is the overall subject of the entity set, whilst the entity set is within the entity which holds the attributes of the entity’s type. For example, in an entity called “Car”, an entity set would consist of attributes “Car ID”, “Car color”, “Car model” and “Car brand”. To explain this better, here is a visual representation. 

Figure \(\PageIndex{1}\): ERD Component. ("Module_3: Mapping ER to Schema, Normalization" by Dr Sarah North, Affordable Learning Georgia is licensed under CC BY 4.0)

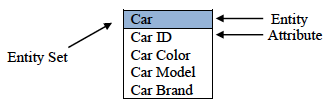
The next important step in understanding ER mapping is attributes. These components are properties which define the entity type. There are many examples to describe this, including Name, DOB, Address, etc. The attribute that uniquely identifies each entity is called a key attribute, usually identifying each entity with a unique number. In the example above, Car ID would be the key attribute which can also be called “Primary Key” or PK. Car ID is the key attribute because every Car ID is unique and can identify each entity separately without duplicates. For more complex designs, there are multiple types of attributes: Composite attributes (compose of two or many combined attributes), Multivalued Attributes (consists of more than one value) and Derived attributes (attributes derived from other attributes). 

A weak entity is an entity type for which a key attribute can’t be defined. A company can store information of dependents (Parents, Children, Spouse) of an Employee but the dependents don’t exist without employee. 

A relational model for database management system is an approach to managing data using a table structure that is consistent with specific logic and properties. In database systems, there exist relations in a two-dimensional table of data. This typically has multiple named columns and an unknown quantity of rows for data to be entered. There are specific properties that define relations so that they can be easily identified by a user. There are six properties of relations: 

1. Each relation (or table) in a database has a unique name. 
2. Each entry at the intersection of each row and column is atomic
   (or single valued). (There can be only one value associated with each attribute on a specific row of a table; no multivalued attributes are allowed in a relation.) 
3. Each row is unique; no two rows in a relation can be identical. 
4. Each attribute (or column) within a table has a unique name. 
5. The sequence of columns (left to right) is insignificant. The order of the columns in a relation can be changed without changing the meaning or use of the relation. 
6. The sequence of rows (top to bottom) is insignificant. As with columns, the order of the rows of a relation may be changed or stored in any sequence. 

As stated previously, these relational tables use a certain structure that is consistent with specific logic and properties: this is called normalization. This process is a technique in database design that is used to organize tables in a manner that reduces redundancy and dependency of data. The use of this technique divides larger tables into smaller tables and links them using relationships. The creator of the relational model, Edgar Codd, came up with the theory of normalization with the introduction of the First Normal Form and then continued to extend this theory into a second and third normal form. 

The first normal form, like all normal forms, has specific requirements to be validated as first normal form. A table in first normal form must be two dimensional with rows and columns, each row must contain data that pertains to something, each column must contain data for a single attribute of the thing it’s describing, each cell of the table must have only a single value, entries in any column has to have the same type of data (Ex. If the entry in one row of a column contains hair color, all the other rows must contain hair color as well), each column must have a unique name, all rows should be uniquely identified (has to have some unique ID), and the order of the columns and rows has no significance. Tables in first normal form are subject to deletion and insertion anomalies and may prove useful in some applications but can be unreliable in others. 

Figure \(\PageIndex{2}\): 1^st Normal Form. ("Module_3: Mapping ER to Schema, Normalization" by Dr Sarah North, Affordable Learning Georgia is licensed under CC BY 4.0)

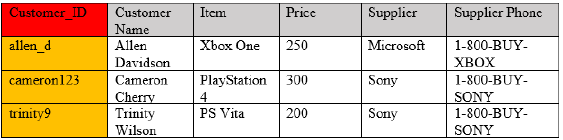
 Second Normal Form 

Must have all attributes or non-key columns dependent on the key. 

Figure \(\PageIndex{3}\): 2^nd Normal From. ("Module_3: Mapping ER to Schema, Normalization" by Dr Sarah North, Affordable Learning Georgia is licensed under CC BY 4.0)

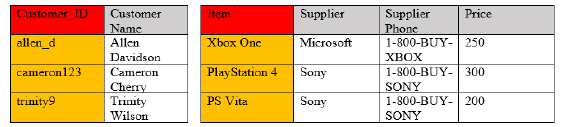
Third Normal Form 

All columns can be determined only by the key in the table and no other column. 

Figure \(\PageIndex{4}\): 3^rd Normal From. ("Module_3: Mapping ER to Schema, Normalization" by Dr Sarah North, Affordable Learning Georgia is licensed under CC BY 4.0)

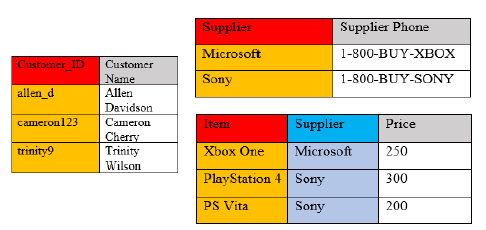
Having this type of normalization gets rid of redundancy and is especially vulnerable to some types of modification anomalies. If Sony were to have more products under their item key, the supplier phone number would keep repeating because it’s directly related to the supplier name and will always be that same phone number. Separating these two tables into individual representations makes all of the columns dependent on only the key in the table and no other 

column, making the third normal form valid. 

Candidate keys are a collective of attributes that identify a database record in a unique way without referencing any other key data from the database. A table may contain one or more candidates and one of those candidate keys has to be referred to as the primary key. The absolute requirement for a table to have is the primary key, but the maximum number of candidate keys is unlimited by any constraints.