6.2: A Graph as a Collection of Lists
- Page ID
- 47912
Adjacency list representations of graphs take a more vertex-centric approach. There are many possible implementations of adjacency lists. In this section, we present a simple one. At the end of the section, we discuss different possibilities. In an adjacency list representation, the graph \(G=(V,E)\) is represented as an array, \(\mathtt{adj}\), of lists. The list \(\mathtt{adj[i]}\) contains a list of all the vertices adjacent to vertex \(\mathtt{i}\). That is, it contains every index \(\mathtt{j}\) such that \(\mathtt{(i,j)}\in E\).
int n;
List<Integer>[] adj;
AdjacencyLists(int n0) {
n = n0;
adj = (List<Integer>[])new List[n];
for (int i = 0; i < n; i++)
adj[i] = new ArrayStack<Integer>(Integer.class);
}
(An example is shown in Figure \(\PageIndex{1}\).) In this particular implementation, we represent each list in \(\mathtt{adj}\) as an ArrayStack, because we would like constant time access by position. Other options are also possible. Specifically, we could have implemented \(\mathtt{adj}\) as a DLList.
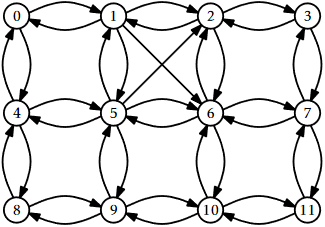
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 2 | 0 | 1 | 5 | 6 | 4 | 8 | 9 | 10 |
| 4 | 2 | 3 | 7 | 5 | 2 | 2 | 3 | 9 | 5 | 6 | 7 |
| 6 | 6 | 8 | 6 | 7 | 11 | 10 | 11 | ||||
| 5 | 9 | 10 | |||||||||
| 4 |
The \(\mathtt{addEdge(i,j)}\) operation just appends the value \(\mathtt{j}\) to the list \(\mathtt{adj[i]}\):
void addEdge(int i, int j) {
adj[i].add(j);
}
This takes constant time.
The \(\mathtt{removeEdge(i,j)}\) operation searches through the list \(\mathtt{adj[i]}\) until it finds \(\mathtt{j}\) and then removes it:
void removeEdge(int i, int j) {
Iterator<Integer> it = adj[i].iterator();
while (it.hasNext()) {
if (it.next() == j) {
it.remove();
return;
}
}
}
This takes \(O(\deg(\mathtt{i}))\) time, where \(\deg(\mathtt{i})\) (the degree of \(\mathtt{i}\)) counts the number of edges in \(E\) that have \(\mathtt{i}\) as their source.
The \(\mathtt{hasEdge(i,j)}\) operation is similar; it searches through the list \(\mathtt{adj[i]}\) until it finds \(\mathtt{j}\) (and returns true), or reaches the end of the list (and returns false):
boolean hasEdge(int i, int j) {
return adj[i].contains(j);
}
This also takes \(O(\deg(\mathtt{i}))\) time.
The \(\mathtt{outEdges(i)}\) operation is very simple; it returns the list \(\mathtt{adj[i]}\) :
List<Integer> outEdges(int i) {
return adj[i];
}
This clearly takes constant time.
The \(\mathtt{inEdges(i)}\) operation is much more work. It scans over every vertex \(j\) checking if the edge \(\mathtt{(i,j)}\) exists and, if so, adding \(\mathtt{j}\) to the output list:
List<Integer> inEdges(int i) {
List<Integer> edges = new ArrayStack<Integer>(Integer.class);
for (int j = 0; j < n; j++)
if (adj[j].contains(i)) edges.add(j);
return edges;
}
This operation is very slow. It scans the adjacency list of every vertex, so it takes \(O(\mathtt{n} + \mathtt{m})\) time.
The following theorem summarizes the performance of the above data structure:
Theorem \(\PageIndex{1}\)
The AdjacencyLists data structure implements the Graph interface. An AdjacencyLists supports the operations
- \(\mathtt{addEdge(i,j)}\) in constant time per operation;
- \(\mathtt{removeEdge(i,j)}\) and \(\mathtt{hasEdge(i,j)}\) in \(O(\deg(\mathtt{i}))\) time per operation;
- \(\mathtt{outEdges(i)}\) in constant time per operation; and
- \(\mathtt{inEdges(i)}\) in \(O(\mathtt{n}+\mathtt{m})\) time per operation.
The space used by a AdjacencyLists is \(O(\mathtt{n}+\mathtt{m})\).
As alluded to earlier, there are many different choices to be made when implementing a graph as an adjacency list. Some questions that come up include:
- What type of collection should be used to store each element of \(\mathtt{adj}\)? One could use an array-based list, a linked-list, or even a hashtable.
- Should there be a second adjacency list, \(\mathtt{inadj}\), that stores, for each \(\mathtt{i}\), the list of vertices, \(\mathtt{j}\), such that \(\mathtt{(j,i)}\in E\)? This can greatly reduce the running-time of the \(\mathtt{inEdges(i)}\) operation, but requires slightly more work when adding or removing edges.
- Should the entry for the edge \(\mathtt{(i,j)}\) in \(\mathtt{adj[i]}\) be linked by a reference to the corresponding entry in \(\mathtt{inadj[j]}\)?
- Should edges be first-class objects with their own associated data? In this way, \(\mathtt{adj}\) would contain lists of edges rather than lists of vertices (integers).
Most of these questions come down to a tradeoff between complexity (and space) of implementation and performance features of the implementation.

