8.1: Activity 1 - Searching Techniques
- Last updated
- Save as PDF
- Page ID
- 47926
Introduction
Searching is one of the most fundamental problems in Computer Science. It is the process of finding a particular item in a collection of items. Typically, a search answers whether the item is present in the collection or not. For simplification for all our examples, we will be taking an array as the collection. This activity will present two searching methods: the sequential search and the binary search methods.
Activity Details
Sequential Search
Sequential (linear) search is the simplest method to solve the searching problem. It finds an item in a collection by looking one item at a time from the beginning to end of collection if it does not find it. Basically, it checks each item in the sequence until the desired element is found before all the elements of the collection are exhausted.
The code snapshot below presents a linear search method.
bool linearSearch (int A[], int length, int item) {
for (int i = 0 ; i < length ; ++i)
if (item == A[i])
return true; // Item is found in array A
return false; // Item is not found in array A }
Consider an array A = {1, 9, 2, 4, 6, 3, 7, 5, 8, 0} and suppose that we wish to find 3 from the given array. The linear search starts from the beginning and checks if current item matches with the item we are searching. In the provided example the item = 3 and the array length = 10.
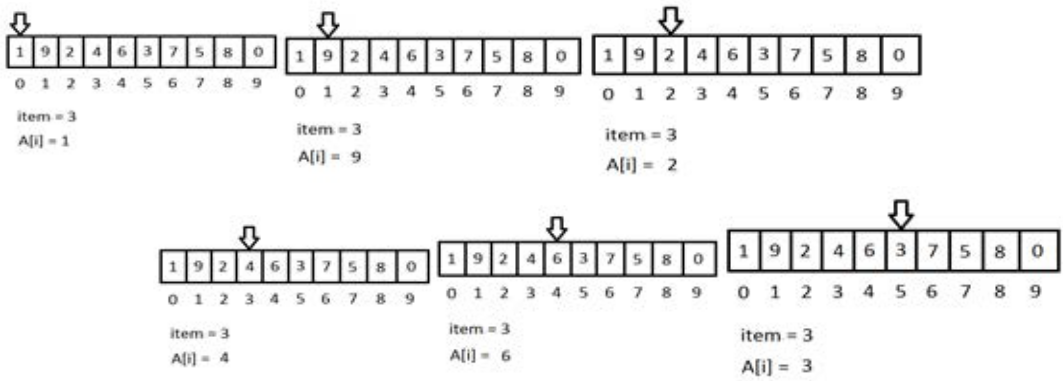
Figure 2.1.1 shows the trace of the sequential search algorithm to find item 3. Note that for i = 0, A[i] = 1 and the item being sought is not equal to A[i]. Similarly, for i = 1, A[i] = 9 and item is not equal to A[i], for i = 2, A[i] = 2 and item is not equal to A[i], for i = 3, A[i] = 4 and item is not equal to A[i] and for i = 4, A[i] = 6 and item is not equal to A[i]. But for For i = 5, A[i] = 3 and item is equal to A[i]. Therefore, the linearSearch() function will return true showing that the item is found. Note that, if the item = 10, linearSearch() function will iterate over all the elements in the array A, and return false (showing that the item is not found), because the ‘if’ condition will never be true.
Now, let us consider the modified search where we need to return the position, where the item is found. To solve this modified search problem, we just need to change two lines in the linearSearch() function as shown below:
int linearSearch ( int A[ ], int length, int item) {
for (int i = 0; i < length ; ++i)
if (item == A[i])
return i; //Returning the index of the element found.
return -1; // Item is not found in array A
}
In the above codes -1 denotes that the item is not found. Note that if there are duplicate elements, the above code will return the first occurrence of the item. The time complexity of linear search is O(size of the array).
Binary Search
Binary Search is a divide and conquer algorithm. In divide and conquer, a larger problem is reduced into smaller sub-problems recursively until the problem is small enough that the solution is trivial. Unlike sequential search, binary search requires that the input array be a sorted array. If the array is sorted in ascending order, binary search compares the item with the middle element of the array. If the item matches, then it returns true. Otherwise, if the item is less than the middle element then it will recursively search on the sub-array to the left of the middle element or if the item is greater it will recursively search on the sub-array to the right of the middle element. Therefore, at each step the size of array will be reduced to half. After repeating this recursion, it will eventually be left with a single element.
The pseudocode for the binary search algorithm is presented below:
Algorithm binarySearch(A, left, right, item) {
if left is less than or equal to right then :
mid = (left + right) / 2
if A[mid] is equal to item then return true
else if item is less than A[mid] then recursively search on the left sub-array
else if item is greater than A[mid] recursively on the right sub-array
else
return false }
Remember that an array should be sorted for the binary search to work!! A recursive implementation of binary search is presented below:
//Recursive Binary Search
bool binarySearchRecur(int A[], int left, int right, int item)
{
if (left <= right)
{
int mid = left + (right - left) / 2; // finding middle index
if (A[mid] == item)
return true; // item found
else if (item < A[mid])
{
// recursively search on the left sub-array
return binarySearchRecur(A, left, mid-1, item);
}
else
{
// recursively search on the right sub-array
return binarySearchRecur(A, mid+1, right, item);
}
}
else
return false; // item not found )
Similarly, an iterative implementation of binary search is given below:
//Iterative Binary Search
bool binarySearchIter(int A[], int length, int item)
{ int left = 0, right = length - 1, mid;
while (left <= right)
{ mid = left + (right - left) / 2; // finding middle index
if (A[mid] == item)
return true; // item found
else if (item < A[mid])
right = mid - 1; // search on left sub-array
else
left = mid + 1; // search on right sub-array
}
return false; // item not found }
Suppose now we are given array A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} and we need to find 3 in the array A. Therefore, we have that search item = 3 and array length = 10. Table 2.1.1 traces the execution of the iterative binary search for item =3 on array A. Note that initially left = 0 and right = length – 1 = 10 – 1 = 9. Figure 2.1.2 depicts that the array diminishes during iterations.
Table 2.1.1 : A trace for Iterative Binary Search on array A
|
Iteration |
left |
Right |
mid |
Remarks |
|---|---|---|---|---|
|
1 |
0 |
9 |
mid = left + (right – left) / 2 = 0 + (9 – 0) / 2 = 4 |
A[mid] = 4 is greater than item. Since the array A is sorted we conclude that the item being found is in the left sub-array |
|
2 |
0 |
mid – 1 = 4 –1 = 3 |
left + (right – left) / 2 = 0 + (3 – 0) / 2 = 1 |
mid = A[mid] = 1 is smaller than item. Since the array A is sorted the item must be in the right sub-array. |
|
3 |
mid + 1 = 1 + 1 = 2 |
right = 3 |
left + (right – left) / 2 = 2 + (3 – 2) / 2 = 2 |
mid = A[mid] = 2 is smaller than item. Since the array A is sorted we can say that the item must be in the right sub-array |
|
4 |
mid + 1 = 2 + 1 = 3 |
right = 3 |
mid = left + (right – left) / 2 = 3 + (3 – 3) / 2 = 3 |
A[mid] = 3 is equal to the item, so the binarySearchIter() function will return true and the item is found |
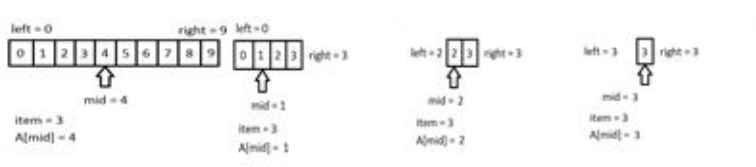
Time complexity of both binarySearchRecur() and binarySearchIter() is O(logN) where N is the size of the array. This is because after each recursion or iteration the size of problem is reduced into half.
Conclusion
In this activity we presented two search algorithms, sequential search and binary search. The sequential search method is based on exhaustive search strategy while the binary search method is based on divide and conquers search strategy. Binary search also requires that the input array to be sorted.
Assessment
- Modify the linearSearch() function discussed in this activity such that it will return the last occurrence of the item, if the item is in the array, otherwise, return -1. (Hint: Store the position of the last found occurrence of the item and update it as soon as the item occurs again).
- Suppose you are given a sorted array with possible duplicate elements within it. Write the code segment that finds the first occurrence of a given input item (assuming the given item exists in the given array).


