7.7: for loops with break Logic
- Page ID
- 84437
By Carey A. Smith
Converging Series with if and break Logic
A series is the sum of the terms of a sequences. They are typically computed with for loops.
(When the terms of the sequence have already been computed, then the series can be computed with the sum() function. This is an example of how MATLAB can simplify a calculation.)
A series is convergent (or converges) if the sequence of its partial sums tends to a limit. (https://en.Wikipedia.org/wiki/Convergent_series) Maclaurin's series generally converge for values of x near zero. (A Maclaurin series is a Taylor series derived for points near 0.)
This subsection describes for loops that are terminated when the terms become very small. Not all series whose terms become small are convergent.
The MATLAB keyword "break" terminates the execution of a for loop or a while loop. In nested loops, break exits only from the loop in which it occurs. Control passes to the statement that follows the end of that loop.
Consider the summation of this power series
where an = (3/(n+1))
Since sum() is an important built-in function, we won't use "sum" as a variable. We will use "total" instead.
Although this series has an infinite number of terms, the terms will get very small as n gets large.
We will end the summation when the absolute value of nth term is < 0.0001
.
Solution
% This is a script to sum a power series
x = 0.3; % This is a precondition
total = 0; % Initialize total before the loop.
term_limit = 0.0001;
for n = 1:1000
term = (3/(n+1))*x^n;
total = total + term;
if(abs(term) < term_limit)
break;
end
end
disp(['Loop broke at n = ',num2str(n)])
disp(['Power Series total = ',num2str(total)])
This code displayed these messages:
Loop broke at n = 7
Power Series total = 0.56672
.
The cosine Maclaurin series starts with these terms:
\[cos x = 1 - \frac{x^2}{2}+\frac{x^4}{24}-\frac{x^6}{720} ...\]
The index of the for loop is m.
This terms in this series have alternating signs, which we get by multiplying by (-1)^m.
(-1)^m = -1 when m is odd, and (-1)^m = 1 when m is even.
This series has only even powers of x, so we will use k = 2* m for the powers.
The \(m^(th)\) term of the cosine Taylor's series is: \( (-1)^m * \frac{x^k}{k!}\)
The break keyword will terminate the sum when abs(terms(m)) < 0.001
Here's the function:
function cos1 = my_cos(x)
% Taylor's series approximation
terms = zeros(1,100); % preallocate
% Usually a the total for a summation is initialize to 0.
% For the cosine series, the term for m = 0 is 1, becuz x^0 = 1, factorial(0) = 1.
So we initialize cos1 (the total) = 1.
cos1 = 1; % Initialize sum of terms in the Taylor's series
terms(1) = cos1;
for m = 1:100 % n = m-1
k = 2*m; % Only even powers of x are used
terms(m) = (-1)^m*x^k/factorial(k);
% Note that (-1)^m = -1 when m is odd
% and it = 1 when m is even.
cos1 = cos1 + terms(m);
if(abs(terms(m)) < 0.001) % Terminate the series when terms(m) is small
break;
end
end
Solution
Add example text here.
.
Convergent Series Homework 1
Write a script that uses a for loop to sum the terms of the series whose mth term = \(\frac{1}{m^2}\)
Use "total" as the variable name. Do not use "sum" as a variable name, because that is an important built-in function.
Initialize total = 0 before the for loop.
Write a for loop that starts with:
for m = 1:1000
Break the for loop when the absolute value of term is < 0.0002
- Answer
-
Add texts here. Do not delete this text first.
.
Diverging Series with if and break Logic
This subsection describes for loops that are terminated when the terms become very large.
Divergent for loop
clear all; close all; format compact; clc;
n = 40; % maximum number of iterations
total = zeros(1,(n+1));
term_lim = 10; % Terminate the sequence if termk > term_lim
for k = 2:n
termk = (-1)^k*(k^2)/(k+30);
if( abs(termk) > term_lim)
disp(['k= ',num2str(k),', termk = ',num2str(termk),...
'>10, so break the loop'])
break;
else
total(k) = total(k-1) + termk;
end
end
figure;
plot(total)
Solution
The plot should look like this figure:
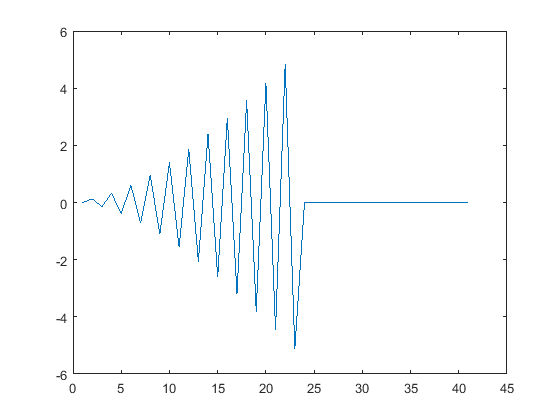
Figure \(\PageIndex{i}\): Divergent for loop
A series can diverge, even though the terms become small. The harmonic series is an example of a series which diverges because the terms do not become small fast enough. This is an example
\[harmonic = \frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}...\]
Homework Exercises
TBD
.



