11.7: Dot Product

By Carey Smith

The dot product is the sum of the products of the corresponding elements of 2 vectors. Both vectors have to be the same length. Geometrically, it is the product of the magnitudes of the two vectors and the cosine of the angle between them.

 

 Figure \(\PageIndex{1}\): a*cos(θ) is the projection of the vector a onto the vector b.

Relationships:

a·b = |a|*|b|*cos(θ)

cos(θ) = |a|*|b| / (a·b)

The dot product of a vector with itself is the sum of the squares of the vector's elements. The vector's magnitude (length) is the square root of the dot product of the vector with itself.

This video gives details about dot product:

.

Here are examples illustrating the cases of parallel vectors, perpendicular vectors (a.k.a orthogonal), and vectors at 60 degrees relative to each other.

Example \(\PageIndex{1}\) Use dot() to compute the magnitude of a vector

a = [1 2 3];
a_dot_a = dot(a,a) % This is the sum of the squares of the elements of A
% 14
a_mag = sqrt(a_dot_a)
% 3.7417

MATLAB also has this function to compute the magnitude of a vector:

a_mag = norm(a)

The norm function computes the square root of the sum of the squares of the elements of the vector.

Solution

Add example text here.

The dot product of 2 different vectors is equivalent to the product of each vector's magnitude (length) times the cos(angle between the 2 vectors).
When the vectors are parallel, the cos = 1, so the dot product = the product of their magnitudes.
When the vectors are perpendicular, the cos = 0, so the dot product = 0.

Example \(\PageIndex{2}\) dot(a,b), a & b parallel

a = [1 2 3];
b = 2*a % = [2 4 6]
ab_dot = dot(a,b)
% = 1*2 + 2*4 + 3*6 = 28
|a| = sqrt(1^2 + 2^2 +3^2) = sqrt(14)
|b| = 2*|a| = 2*sqrt(14)
|a|*|b| = 2*14 = 28

Solution

Add example text here.

.

Example \(\PageIndex{3}\) dot(c1,d1), c1 & d1 perpendicular: 0 & 90 degs

c1 = [1 0 0] % 0 degs
d1 = [0 1 0] % 45 degs
cd1_dot = dot(c1,d1)
% = 0, so these are perpendicular

Solution

Add example text here.

.

Example \(\PageIndex{4}\) dot(c2,d2), c2 & d2 perpendicular: +/- 45 degs

c2 = [ 1 1 0] % at 45 degs
d2 = [ 1 -1 0] % at -45 degs
cd2_dot = dot(c2,d2)
% = 0, so these are perpendicular

Solution

Add example text here.

.

Example \(\PageIndex{5}\) dot(e1,f1), unit vectors at 0 & 60 degrees

e1 = [ 1 0 0] % unit vector at 0 degs
f1 = [ cosd(60) sind(60) 0] % unit vector at 60 degs
% f1 = [0.500 0.866 0]
ef1_dot = dot(e1,f1)
% = 0.500 = cosd(60)

Solution

Add example text here.

.

Example \(\PageIndex{6}\) Not unit vectors at 0 & 60 degrees

e2 = 2*[ 1 0 0] % at 0 degs
e2_mag = sqrt(dot(e2,e2)) % = 2
f2 = 5*[ cosd(60) sind(60) 0] % at 60 degs
f2_mag = sqrt(dot(f2,f2)) % = 5

% When they are not unit vectors, we need to divide by their magnitudes.
cos_ef = dot(e2,f2) / (e2_mag*f2_mag)
% = 0.5 = cos(60)

Solution

Add example text here.

.

Example \(\PageIndex{7}\) Use dot product to find the angle between 2 vectors

%% dot_product_cos
% Define these 2 vectors:
a = [2, 1.5, 0]
b = [4, 0 ,0]
% Plot the vectors
figure;
plot([0, a(1)], [0, a(2)], 'b', 'LineWidth', 3)
hold on;
plot([0, b(1)], [0, b(2)], 'r', 'LineWidth', 3)
grid on;
axis equal;
legend('a', 'b')

%% Find the angle between them
a_mag = norm(a)
b_mag = norm(b)
cos_ab = dot(a,b)/(a_mag*b_mag)
theta_degs = acosd(cos_ab) % degrees

%% Draw an arc for the included angle
r = 1; % radius of the arc
ang_vector = linspace(0, theta_degs, 9);
ax = r*cosd(ang_vector);
ay = r*sind(ang_vector);
plot(ax, ay, 'k')
text(1.1, 0.3, '\theta', 'FontSize',16)

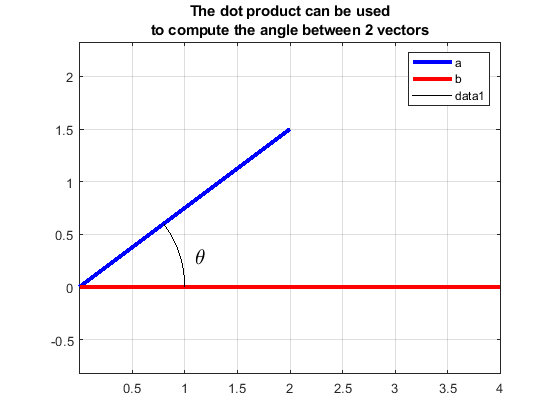
Figure \(\PageIndex{2}\): Dot product can be used to compute the angle between 2 vectors.

Solution

Add example text here.

.

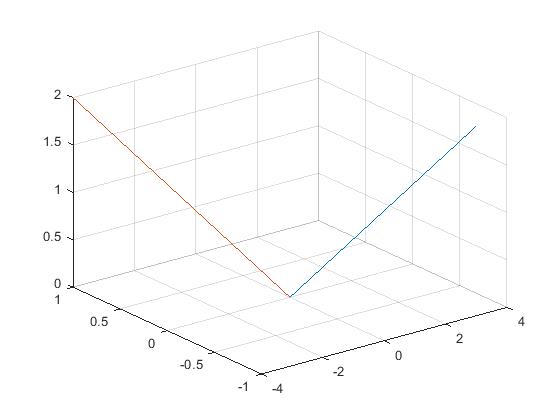
Dot Product in 3 dimensions

The dot product can also be computed for 3-D vectors. Consider:

v1 = [a, b, c]

v2 = [x, y, z]

Then dot(v1, v2) = a*x + b*y + c*z

The plot3() function syntax is plot(x, y, z).

Example \(\PageIndex{8}\)

v1 = [3 -1 2];

v2 = [-4 1 2];

figure;
plot3([0,v1(1)], [0, v1(2)], [0, v1(3)])
grid on;
hold on;
plot3([0,v2(1)], [0, v2(2)], [0, v2(3)])

dp12 = dot(v1,v2)   % = 3*(-4) + (-1)*1 + 2*2 = -9

mag_v1 = sqrt(dot(v1,v1))  % 3.74
mag_v2 = sqrt(dot(v2,v2))  % 4.58

cos_theta = dp12 / (mag_v1 * mag_v2)  % -0.5249

theta = acosd(cos_theta)   % = 121.7 degrees

Solution

Add example text here.

.

Example \(\PageIndex{9}\) Headwind Calculation Using the Dot Product

% A jet has heading of alpha = 20 degs.
alpha = 20; % degs
% What is the heading unit vector? 
B = [cosd(alpha), sind(alpha), 0] % unit vector
% B = [ 0.9397    0.3420   0]
% The wind is 30 km/s at an angle of 150 degs. So its vector is 
wind_vel = 30; % km/s
wind_ang = 150 % degs
A = wind_vel*[cosd(wind_ang), sind(wind_ang), 0] 
% A = [-25.9808  15.0000  0]
% What is the component of wind along the jet’s heading? 
%Answer: 
head_wind = dot(A, B)  
% head_wind = -19.2836

Solution

Add example text here.

.