12.5: Systems of Equations Examples and Exercises

Last updated
Save as PDF

Page ID: 85166

Carey Smith
Oxnard College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

By Carey A. Smith

Exercise \(\PageIndex{1:}\) Solving Linear Equations Video and Homework

Watch this 4 minute video. Then code up the example shown and solve using Matlab's inv() function.

Helps:

(1) Define the matrix A shown in the video.

(2) Define the vertical vector B shown in the video.

(3) X is the unknown vertical vector whose elements are x and y

Answer

X = inv(A)*B

Test your answer by computing:

B2 = A*X

You should get B2 == B

This video shows how to solve a system of equations graphically.

Example \(\PageIndex{1:}\) 2 equations, 2 unknowns Graphic and Matrix methods

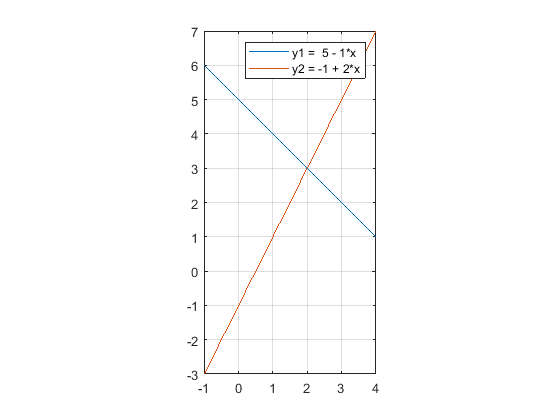
1*x + y = 5
-2*x + y = -1

1a. Graphical Solution

Each of 2 equations in 2 unknowns, x and y, can be plotted as a line. Their intersection is a graphical solution of the 2 equations. The equations and their plot is shown here. The intersection is the point (2, 3). So the solution of this system of equations is x=2, y = 3.

1b. Solution using the matrix inverse.

Matrix formulation:

% A*xy = B
A = [ 1 1
-2 1]
% xy = [x
% y]
B = [ 5
-1]
rank(A) % 2 (full)
det(A) % 3 (non-zero)
% Method 1: Solution using the inverse of A:
% inv(A)*A*xy = inv(A)*B
% inv(A)*A = I, so
xy = inv(A)*B

% Solution = (2, 3), same as above

1b. Solution using left matrix-division .

Same formulation as in part 1b. The left matrix-division conceptual derivation is:

A*xy = B
(1/A)(A*xy) = (1/A)*B [Not B/A--not commutative]

Write (1/A)*B as xy = A\B

% Solution = (2, 3), same as above

Solution

The solutions were given in the example.

Important note about left matrix-division:

xy = A\B is “Left Matrix-Division”. It solves the system of equations by Gaussian Elimination, which is a series of matrix operations. When A is a 3x3 matrix and B is a 3x1 vector, then the result, xy, is a 3x1 vector.

Unfortunately, MATLAB has another function, ldivide(), which sounds like it is the same thing, but it is not. Do not use ldivide(); it does an element-by-element divide, rather than a matrix operation. When A is a 3x3 matrix and B is a 3x1 vector, then the result of using ldivide(), xy is a 3x3 matrix, which is not the solution of the system of equations.

So use either

xy = A\B

xy = inv(A)*B

Exercise \(\PageIndex{2:}\) System_of_Equations_HW2

Given this system of equations:

1*x + 1*y + 2*z = 11.1
0*x -1*y + 3*z = 5.4
4*x + 2*y + 1*z = 9.7

Solve for x, y, and z using the following steps:

Part 1 (3 pts). Create the matrix, M, of the coefficients.

Part 2. (1 pt). Create the right-hand side vector of constants. Call it R.

Part 3. (1 pt). Compute the determinant and verify that it is not 0

Part 4. (3 pts) Let xyz = the vector of unknown values of x, y, and z. Solve for xyz using the inverse of M.

Part 5: (3 pts) Solve for xyz using the inverse of M, using left matrix-division.

Part 6: (1 pt) Multiply M*xyz and verify that it equals R.

Answer: The answer is not given here.

.
This video shows how systems of equations are used to solve a structural engineering truss problem:

Example \(\PageIndex{2:}\) Electric_Circuit_KVL1

You do not need to to be a circuits expert. The equations needed will be given to you. Then these will be put in the form of a system of linear equations that can be solved.

Kirkoff’s Voltage Law:

The sum of the voltages around any loop without a voltage source = 0.

The sum of the voltages around any loop with a voltage source = the voltage of the source.

When a resistor is part of 2 loops, the sum of the currents across the resistor needs to be used. We assume that the current is positive in the direction of the arrows in the drawing. When the direction of the loop arrow is backwards through a resistor, then use the negative of voltage across the resistor.

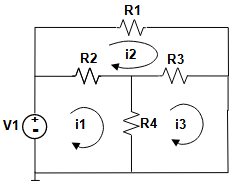
The voltage supply is V1 = 3 volts.

The resistors are:

R1 = 1 Ohm

R2 = 2 Ohms

R3 = 3 Ohms

R4 = 4 Ohms

The expressions for the voltages across each resistor are:

We use the formula: V = R*I, where V = voltage, R = resistance, I = current.

VR1 = R1*I2 %Voltage across R1 (left to right)
VR2 = R2*(I1 - I2) %Voltage across R2 (left to right)
VR3 = R3*(I3 - I2) %Voltage across R3 (left to right)
VR4 = R4*(I1 - I3) %Voltage across R4 (top to bottom)

The voltages around each loop are:

R2*(I1 - i2) + R4*(I1 – i3) = V1 %Loop1

R1*I2 - R3*(I3 - I2) - R2*(I1 - I2) = 0 %Loop2

R3*(I3 - I2) - R4*(I1 - I3) = 0 %Loop3

Since the unknowns are the currents, I1, I2, I3, we combine like terms, so that we can put this in matrix form:

(R2+R4)*I1 (-R2)*i2 + (-R4)*i3 = V1 %Loop1
(-R2)*I1 + (R1+R2+R3)*i2 + (-R3)*i3 = 0 %Loop2
(-R4)*I1 + (-R3)*i2 + (R3+R4)*i3 = 0 %Loop3
The matrix form is coef*I123 = vconst, where:

coef = [(R2+R4), (-R2), (-R4);
(-R2), (R1+R2+R3), (-R3);
(-R4), (-R3), (R3+R4)]

I123 = the vector of the unknown currents.

vconst = [V1;
0;
0]
The computed value of matrix coef is:

% 6 -2 -4
% -2 6 -3
% -4 -3 7

det(coef) % = 26, so coef is non-singular.

We can now solve for I123 using either the inverse of coef or using left-matrix division.

Once we have computed I123, we can compute the currents in each loop and the voltages across each resistor.

Solution

Using the inverse of coef:

I123 = inv(coef)*vconst
% 3.8077
% 3
% 3.4615

Using left matrix division:
I123 = coef\vconst %Same answer to 5 significant figures

Check the answer by computing the matrix form:
check1 = coef*I123

This equals the right-hand-side, vconst.

We can use I123 to compute the currents in each loop:

I1 = I123(1)
I2 = I123(2)
I3 = I123(3)

We can use these currents to compute the voltages across each resistor:

VR1 = R1*i2 %Voltage across R1 (left to right)
VR2 = R2*(I1 - i2) %Voltage across R2 (left to right)
VR3 = R3*(i3 - i2) %Voltage across R3 (left to right)
VR4 = R4*(I1 - i3) %Voltage across R4 (top to bottom)

Then we can verify that the sums of the voltages around each loop are essentially zero:
VLoop1 = -V1 + VR2 + VR4
VLoop2 = VR1 - VR3 - VR2
VLoop3 = VR3 - VR4

Exercise \(\PageIndex{3:}\) Electric_Circuit_KVL2

Kirkoff’s Voltage Law:

The sum of the voltages around any loop without a voltage source = 0.

The sum of the voltages around any loop with a voltage source = the voltage of the source.

This circuit is similar to the previous example. R3 has been removed and R5 has been added. The values of the voltage and the resistances have been changed.

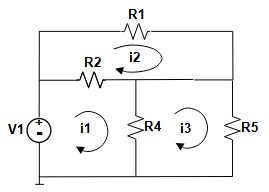
The voltage supply is V1 = 6 volts.

The resistors are:

R1 = 12 Ohms

R2 = 6 Ohms

R4 = 3 Ohms

R5 = 6 Ohms

Use this formula: V = R*I, where V = voltage, R = resistance, I = current.

The expressions for the voltages across each resistor are:

VR1 = R1*I2 %Voltage across R1 (left to right)
VR2 = R2*(I1 - I2) %Voltage across R2 (left to right)
VR4 = R4*(I1 - I3) %Voltage across R4 (top to bottom)
VR5 = R5*I3 %Voltage across R5 (top to bottom)

The voltages around each loop are:

R2*(I1 - I2) + R4*(I1 - I3) = V1 %Loop1
R1*I2 - R2*(I1 - I2) = 0 %Loop2
R5*I3 - R4*(I1 - I3) = 0 %Loop3

Since the unknowns are the currents, I1, I2, I3, we combine like terms, so that we can put this in matrix form:

(R2+R4)*I1 (-R2)*i2 + (-R4)*i3 = V1 %Loop1
(-R2)*I1 + (R1+R2+R3)*i2 + (-R3)*i3 = 0 %Loop2
(-R4)*I1 + (-R3)*i2 + (R3+R4)*i3 = 0 %Loop3
The matrix form is coef2*I123 = vconst, where:

coef2 = [(R2+R4), (-R2), (-R4);
(-R2), (R1+R2+R3), (-R3);
(-R4), (-R3), (R3+R4)]

I123 = the vector of the unknown currents.

vconst2 = [V1;
0;
0]
Compute the determinant of the coef2 matrix.

Compute I123 using either the inverse of coef2 or using left-matrix division.

Check the computed value of I123 by computing the matrix form:
check2 = coef2*I123

This should equal the right-hand-side, vconst2.

Use I123 to compute the voltages across each resistor:

Verify that the sums of the voltages around each loop are essentially zero:
VLoop1 = -V1 + VR2 + VR4
VLoop2 = VR1 - VR3 - VR2
VLoop3 = VR3 - VR4

Answer: The answer is not given here.

Exercise \(\PageIndex{4}\) Metal Alloy System of Equations

An engineer has samples of 3 Magnesium-Aluminum-Zinc alloys.

These alloys are named Az63, Az92, and Az92 (The 2 numbers represent the percentages of Aluminum and of Zinc)

% The fractions of each metal in each alloy are given in this table:
% | AZ63 | AZ91 | AZ92 |
% ---|------|------|------|
% Mg | 0.91 | 0.90 | 0.89 |
% Al | 0.06 | 0.09 | 0.09 |
% Zn | 0.03 | 0.01 | 0.02 |

Part 1 (3 pts). Create M3 = 3x3 coefficient matrix with these proportions.

Part 2: (1 pt). Compute the determinant of M3. Since the numbers in the table are small, we expect the determinant to be on the order of 10e-4. For this problem, as long as it is > 10e-8, then the matrix is not singular and can be properly inverted.

Part 3 (2 pts). The engineer wants to combine one sample of each of the 3 alloys, such that the combination has the following weights of each metal (which is written as a vector W3):

W3 = [16.11 % Total weight of Mg in the 3 samples
1.560 % Total weight of Al in the 3 samples
0.330]; % Total weight of Zn in the 3 samples

Create the vector W3 in your code.

Part 4 (3 pts) Let S = vector with the unknown weights of the 3 samples. Solve for S using the matrix inverse method.
Part 5 (3 pts) Use inverse or left matrix-division to solve for S using the left-division method.

Part 6. (2 pts) Multply M3 times S and verify that the result = W3

(https://www.azom.com/article.aspx?ArticleID=8675 (Links to an external site.))

Answer: The answer is not given here.

Truss problem