12.2: Matrix Multiplication Applications

By Carey Smith

Rotation Matrices

One use of matrices is to rotate vectors.

A 2D Rotation matrix is of this form:

Mrot2D = [ cosd() -sind() ]

[ sind() cosd() ]

(Use cosd() and sind() when the angle is in degrees.)

Use cos() and sin() when the angle is in radians.)

Example \(\PageIndex{3}\) 2D Rotate by 60 degrees clockwise:

Mrot2D60 = [ cosd(60) -sind(60) ] = [ 0.5 -0.866 ]

[ sind(60) cosd(60) ] [ 0.866 0.5 ]

Example code is in the attached file Ex_Rotation2D.m

Solution

Add example text here.

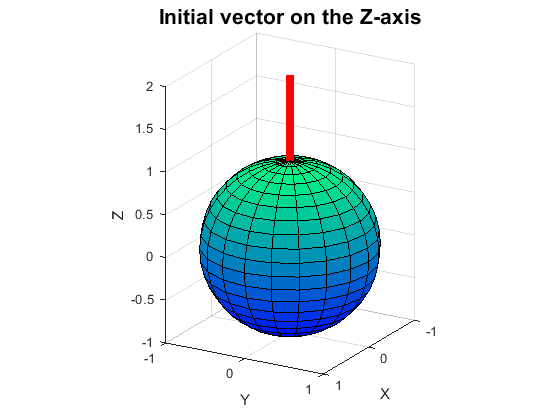
3D Rotation matrices

A 3D Rotation matrix about the z-axis is has a 2D rotation sub matrix in it. It is of this form::

Mrot3Dz = [ cosd(z) -sind(z) 0 ]

[ sind(z) cosd(z) 0 ]

[ 0 0 1 ]

3D Rotation matrix about the X-axis is:

Mrot3Dx = [ 1 0 0 ]

[ 0 cosd(x) -sind(x) ]

[ 0 sind(x) cosd(x) ]

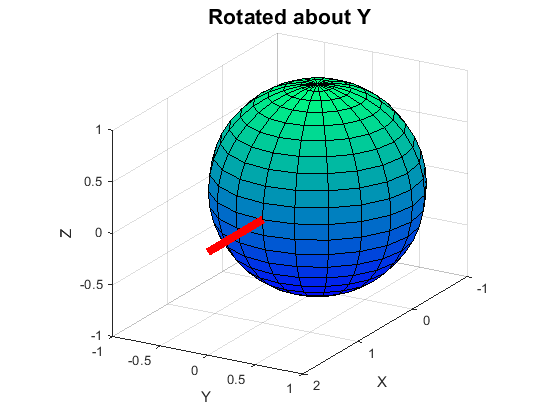
3D Rotation matrix about the Y-axis is:

Mrot3Dy = [ cosd(y) 0 sind(y) ]

[ 0 1 0 ]

[ -sind(y) 0 cosd(y) ]

Example code is in the attached file Ex_Rotation3D.m

This produced the following figures:

Initial vector is on the Z-axis	Rotate by+90 about Y it goes to the X-axis	Rotate by+90 about Z it goes to the Y-axis	Rotate by+90 about X it goes to the Z-axis

Matrix Powers

A matrix can be raised to a power using matrix multiplication.

Example \(\PageIndex{4}\)

A = [1 2
3 4]

A^2 = A*A = [1 2]*[1 2] = [ 7 10]

[3 4] [3 4] [15 22]

A^4 = [199 290]
[435 634]

Solution

Add example text here.

Life Cycle Matrix

A Matrix can be used to model the number of plants or animals at various stages from year to year.

Example \(\PageIndex{5}\) Draba Plant Matrix Life Cycle

This example considers a small flowering plant called Lake Tahoe Draba. Information about this plant and an image is available at: https://calscape.org/Draba-asterophora-(). That image is copyrighted. The image below is a creative commons image of a similar draba species. The numbers used in this example are made up simply to illustrate a possible application of matrix multiplication.

https://commons.wikimedia.org/wiki/F...orullensis.jpg, Tim Park

This file is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.

Consider these stages of a plant:

• Seed
• Seedling (1st year)
• Mature plant

The numbers of plants in each stage will be the elements of a vector, D, for Draba.

Initialize D to have 20 mature plants, with zeros for the other stages:

D1 = [0

      0

      20]

Let T = the transition matrix from 1 year to the next.

Assume the following average numbers: (These are made up)1 plant produces 8 seeds.

Fraction of seeds that become seedlings = 0.2

Fraction of seedlings that become mature plants = 0.5

Fraction of plants that survive from year to year = 0.7

Create the transition matrix's rows:

seeds = 8*number of mature plants:

-> T_seeds = [0 0 8]

seedlings = 0.2*number of mature seeds

-> T_seedlings = [0.2 0 0]

New mature plants from seedling = 0.5*seedlings

0.7*mature plants survive from the previous year

T_mature = [0 0.5 0.7]

The T matrix is created by combining these 3 vectors:

T = [T_seeds

T_seedlings

T_mature ]

T= [0   0   8

    0.2 0   0

    0   0.5 0.7 ]

Compute the numbers of each stage in year 2:

D2 = T*D1

Compute the numbers of each stage in year 3:

D3 = T*D2

Compute the numbers of each stage in year 4:

D4 = T*D3

Compare D4 another way using a matrix power:

D4b = (T^3)*D1

Verify that this produces the same result.

Compute the numbers of each stage in year 10:

D10 = (T^9)*D1

Solution

Add example text here.

.