16.2: Nonlinear Interpolation
- Page ID
- 85394
A smoother interpolation than linear interpolation is called spline interpolation. Originally, a "spline" was a strip of flexible material that could be bent, so that a person could make a smooth curve through data points. The mathematical spline connects the data points with 3rd-order polynomial segments whose 1st and 2nd derivatives are continuous at each point. In MATLAB/Ocatave "spline" is an option with the interp1() function. The next example show how to use it and what the result is.
This data is from Seimers example 40. It shows that the spline is smoother than the linear interpolation.
x1 = 0:5;
y1 = [12,10,9,6,2,0];
figure;
plot(x1, y1, 'o')
grid on
%% Interpolate with linear segments
x2 = 0: 0.1: 5; % Point spacing for plotting the fitted curve
% The default interpolation method is 'linear':
y2 = interp1(x1, y1, x2); % Compute the curve
hold on;
plot(x2, y2)
title('Interpolation with lines between the data points')
%% Interpolate with a smooth spline curve
y3 = interp1(x1, y1, x2, 'spline'); % Compute the curve with the 'spline' option
hold on;
plot(x2,y3,'r')
title('Interpolation')
legend('data', 'spline')
Solution
.
Another 3rd-order interpolation method in MATLAB is "pchip". The difference is the assumptions on the derivatives in the 2 end segments. The pchip is a newer algorithm and is often preferred over the spline.
Pchip interpolation is compared to spline interpolation in this example, using the same data and spline as in the previous example.
figure;
plot(x1,y1,'o')
grid on
y3 = interp1(x1, y1, x2, 'spline'); % Compute the curve
hold on;
plot(x2,y3,'r')
title('Interpolation')
%% Interpolate with a smooth pchip fit
y3 = interp1(x1, y1, x2, 'pchip'); % Compute the curve with the 'pchip' option
plot(x2,y3,'b')
title('Interpolation')
legend('data', 'spline', 'pchip')
% 'pchip' and 'spline' only differ in the 2 end segments
Solution
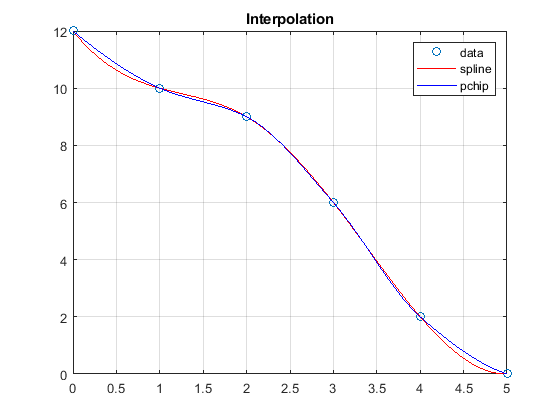
.
Create an m-file script. Define this a, y data set:
x0 = -10:3:10;
y0 = -5 +2*x0 + 0.9*x0.^2 - 0.3*x0.^3;
Open a figure and plot this data using the 'o' marker. (No line)
Use hold on.
Define these x-points at which to compute the interpolated curves:
x2 = -10:0.5 : 10;
Interpolate the data from the x, y data to the x2 values with linear interpolation. Plot the result on the same figure.
Interpolate the data from the x, y data to the x2 values with spline interpolation. Plot the result on the same figure.
Interpolate the data from the x, y data to the x2 values with pchip interpolation. Plot the result on the same figure.
Add a legend and a title.
- Answer
-
The solution is not given here.
There is also the interp2() function for doing interpolation on a 2-dimensional array of data.
Construct this data set:
x0 = -10:3:10;
y0 = -5 + 10*x0 - 2*x0.^3 + 0.1*x0.^4;
Open a figure.
Do the following interpolations and plot them on the same figure: Linear, spline, and pchip.
Add a legend.
Answer
-
The solution is not given here.
.
Go to weather.gov. Enter your zip code. Click on "3 Day History" (under "More Information") and find the temperatures for a recent day for every 3 hours from 6:00 to 21:00 (9 pm).
Open a new figure. Create and plot temperature vs. time (use 24 hour time) with the 's' marker. % (The x-axis is time, the y-axis is temperature.)
Add hold on to your .m file.
Create a new time vector from 6 to 21 with increments of 0.5 hours. Compute the pchip interpolation for this new time vector and plot it as a curve on the same plot.
Put a title with the zip code and the date of the data.
Label the x and y axes. Turn the grid on.
- Answer
-
This is an example. Use your own data. Your data will be different.
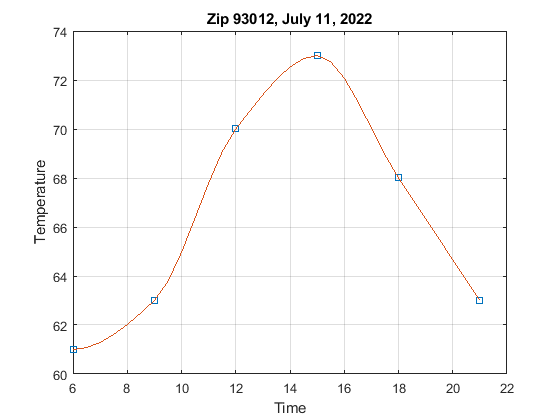
..


