7.4.1: Theoretical Background the Nature of Light and the Photoelectric Effect

How does the PV conversion work? Well, the underlying physics is much more complicated than in the case of CSP conversion. In the latter, things are easy to understand: it’s our everyday experience that solar light carries energy, and when it impinges objects, it heats them up. With PV conversion things are more complicated. But if we wanted to outline a detailed theory of PV conversion, not a single Section would be enough – an entire book would be needed. Therefore, out of necessity, we can present only a “simple-minded theory” of PV conversion in this chapter. By a “simple-minded theory” the Author understand an outline in which everything is true, but a number of things have to be accepted without a proof or based only on a simplified reasoning.

We have to start with the microscopic nature of light. The truth is that this nature seems mysterious to many, because in some phenomena light behaves like a typical wave, and in some other phenomena it behaves like a beam of particle-like objects. We call it a ”dual nature”. Some people riot against such interpretation, insisting that a micro-world object must be either a wave or a particle, because these two “natures” are mutually exclusive. Indeed, they are – but in the macro-world we live in. In the micro-world, which we cannot observe directly with our senses, because the scale is too small, the rules may be different – and a variety of experiments show that they are different, indeed.

The PV conversion is one of those phenomena in which light exhibits its particle-like nature. The physical effect taken advantage of in PV conversion is a version of the photoelectric effect (PE), called internal. The other version, the external PE, was first discovered by Heinrich Hertz in 1887: he observed that light incident on a metallic plate ejects electrons out of it. It caused a big consternation in the community of physicists, because in 1887 the wave-like nature of light seemed to be firmly established – and a wave cannot knock electrons out of a metal! (PAWAP – please accept without a proof). Only after 18 years an explanation of the PE was given by Albert Einstein¹. Einstein’s explanation was based on a courageous hypothesis – namely, that in the PE light behaves like a stream of miniature particle-like objects he called “light quanta” (only some time later people started calling them photons, as we still do today). Some “big names in physics” at that time insisted that Einstein had lost contact with reality. However, with time, new and new facts supporting Einstein’s theory had been discovered, so that eventually it was universally accepted.

The Einstein’s theory of photons, or “light particles”, still “borrows” something from the wave theory of light. Namely, any wave is characterized by a frequency, usually denoted as \( f \). The two other parameters characterizing a wave are the wavelength \( \lambda \) and the speed of propagation \( v \). These three parameters are related as:

\[ f = \dfrac{v}{\lamba} \]

For light, the speed of propagation is always the same, denoted as \( c \), and it’s value is very close to 300,000 km/s. So, the frequency of a light wave is:

\[ f = \dfrac{c}{\lamba} \]

The wavelength \( \lambda \) is different for each light color. And the good news is that \( \lambda \) for a given light color can be readily measured using a simple device called optical grating or diffraction grating – it’s a standard exercise in introductory physics laboratory. And the speed of light \( c \) has been measured with a great precision in zillions experiments, so it’s value is very well known. Therefore, having measured \( \lambda \) for a given light color, we can readily find the characteristic frequency \( f \) of this color.

So, in Einstein’s theory what the photons “share” with the light theory is the frequency \( f \) . But the entirely new element in the theory is that each “light particle”, or each photon carries an amount of energy \( E_{photon} \) equal:

\[ E_{photon} = h \cdot f \]

where \( h \) is an important physical constant, commonly referred to as the Planck Constant.

Accordingly, each individual photon carries some energy. It’s not kinetic energy, because a photon has no mass – but energy it has.

Now, we have to say something about electrons in metals. In 1905, when Einstein published his revolutionary PE paper, the theory of electrons in metals was not even in “its infancy”. However, Einstein correctly assumed that an electron is held inside the metal by some attractive force – therefore, for pulling the electron outside some work has to be done. Einstein called it the work function, and attributed a symbol of \( \Phi \) to it.

What happens, then, if a photon enters the metal²? It may interact with an electron and pass its energy to it – i.e., in the process the photon disappears and its energy \( hf \) is converted to electron’s kinetic energy. After “swallowing” the photon energy, the electron becomes a photoelectron. If the photoelectron energy is lower than the “work function” \( \Phi \, the extra energy acquired by the electron won’t be sufficient to get it out of the metal. But if \( hf \gt \Phi \), the photoelectron can get out and it still retains some of the acquired energy.

Figure \(\PageIndex{1}\): Photoelectric effect in a metal. In metals, the outrmost atomic electrons leave their “parent” atoms and form an “electron gas” (a.k.a. “Fermi gas”). Such electrons may be ejected from the metal by impinging photons of light from the visible or ultraviolet energy range. Atomic electrons from deeper levels are too strongly bound to their parent atoms and cannot be ejected by such photons (source:Wikipedia).

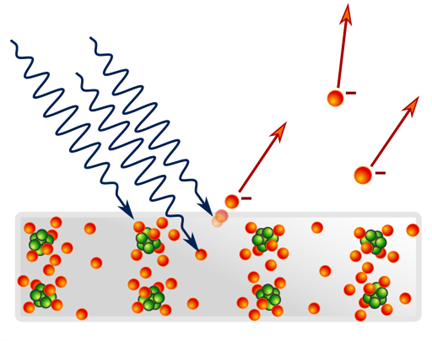
As follow from the above reasoning, the kinetic energy \( K_{el} \)_. of the photoelectron after it gets out of the metal is:

\[ K_{el} = h \cdot f - \Phi \]

It’s the famous Einstein’s equation for the photoelectric effect. For the external photoelectric effect, to be exact – external, because the electron exits the metal.

In the Eq. 7.4, the energy of the photoelectrons should be denoted as \( K_{max} \)_. – why that “max”? Well, when Einstein derived the Eq. 7.4, he probably assumed that the value of \( \Phi \) is the same for all electrons in the metal. However, as it turned out later, there is a distribution of \( \psi \) values for different electrons. What we now call \( \Phi \), is the minimum value of the work function for a given metal. Hence, in the case of Potassium, the work needed to “pull out” an electron from the metal may be 2.0 electron-Volts, or more. Therefore, the \( K_{el} \)_. parameter in the Eq. 7.4 should be thought of as the maximum photoelectron energy, and the photoelectron velocity corresponding to this energy should thought of as the maximum speed of the photoelectron.

How can the energy of photoelectrons be investigated? The apparatus needed for that is very simple.

Figure \(\PageIndex{2}\):

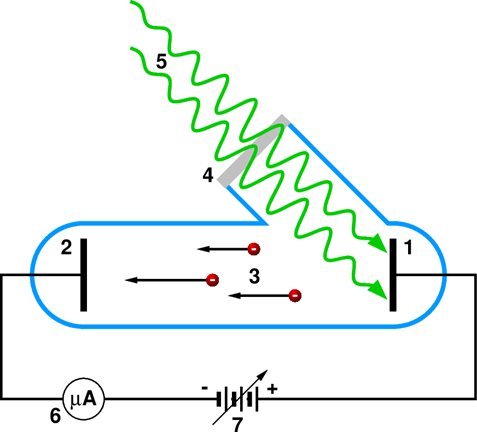
The apparatus used for investigating the photoelectric effect. Inside an evacuated glass tube (blue line) there are: 1 – cathode made of the investigated metal; 2 – anode, the electrode collecting the photoelectrons; 3– photoelectrons; even if all incident photons have the same energy, the kinetic energy of all photoelectrons is not the same – the famous Einstein’s equation describes only the maximum energy. 4 – a quartz window; in contrast to glass, quartz is transparent for ultraviolet (UV) light, so that such window makes it possible to study the effect for UV light. 5 – the photons incident on the catode; 6 – a sensitive current meter; 7 – a variable voltage source (aop).

The electrode made of the metal investigated, called cathode, or photocathode, is placed in an evacuated glass tube, together with another electrode called the anode. The two electrodes are connected to a variable voltage source, enabling one to change the potential between them. Also, there is an ammeter in the circuit for measuring the current of photoelectrons, usually referred to as the photocurrent.

If we want to determine the value of \( \Phi \), we connect the negative terminal of the voltage source to the anode, and the positive terminal to the photocathode, and we start with a zero voltage. After the photocathode is illuminated, photoelectrons are ejected from it. They have certain kinetic energy, so they reach the anode – and so, a current is flowing. Now, we start gradually increase the voltage – i.e., making the anode more and more negative. A negative electrode repels the electrons. So, as the voltage is increased, less and less photoelectrons have their energy high enough to reach the anode, and the current gradually decreases. At some negative voltage \( U_{max}\), the current completely stops flowing.

Now, we only need to recall the definition of the unit of electron-Volt : One electron-Volt, the eV, is equal to the gain or to the loss of kinetic energy of an electron passing trough a potential difference of 1 Volt. Accordingly, if the fastest photoelectrons are stopped by a potential difference of \( U_{max}\), it means that their energy in the units of eV is equal to the\( U_{max}\) in the units of Volts. Very simple, indeed – we get the \( K_{el} \) in Eq. 7.4 just by reading \( U_{max}\) from a voltmeter. And the value of \( hf \) for the light we use we know from other measurement. Then, we get the value of \( \Phi \) by solving the Eq. 7.4: \( \Phi = h \cdot f - K_{el} \) _..

Internal Photoelectric Effect

All the discussion above was about the external PE. But, as mentioned, there is also an internal PE. What’s the difference? Well, if the energy \( h \cdot f \) of photons is lower than \( \Phi \),, any photoelectrons created by such photons have no chance to exit the material. Such is the situation in the case of the red light in the Fig. 7.12. If the red light produces any photoelectrons in Potassium metal, they will stay inside and they will blend into the “crowd” of electrons that are are already there. So, since there is no chance to observe such photoelectrons, there is no much interest among physicists in the internal photoelectric effect in metal.

But there is another family of materials in which such internal photoelectrons do produce conspicuous effects – namely, in semiconductors. What’s important for us, semiconductors are the materials from which PV panels are made. And the internal PE plays a crucial role in the electricity generating process in such panels.

But before we start explaining how the internal PE is taken advantage of in the generation process, we have to explain what semiconductors are, what is the “doping” of semiconductors, and how doped semiconductors conduct electric current.

______________________________________________________

1. It was what for Einstein was awarded with a Nobel Prize in 1921 – not for the relativity theory, as many people wrongly believe.

2. Light is reflected from a metal surface, but the process involves penetration at a depth of the order of nanometers.