7.4.6: Solar Cell Efficiency
- Page ID
- 85126
Solar cell efficiency is the portion of sunlight energy that can be converted into electricity.
Let’s begin our discussion with a description of the spectrum of solar light. It can be divided into three regions:
- infrared (IR) – light with wavelength λ longer than 700 nm, or photons with energy lower than 1.77 eV;
- visible – light with wavelength between 700 nm (red color) and 400 nm (violet color) – or with photon energy between 1.77 eV and 3.10 eV;
- ultraviolet (UV) – with wavelength shorter than 400 nm, and photon energy higher than 3.1 eV.
In solar light, 46% of power is carried by IR photons, 47% by visible light photons, and 7% by UV photons.
Different light wavelengths may contribute in a different way to the output power of a silicon cell. In Si, the minimum energy needed to produce an electron-hole pair (we called that energy as \( \Psi \) in Section 3.4.4) is 1.14 eV. It means that all photons with energies lower than 1.14 eV, and wavelength longer than 1100 nm are not absorbed by silicon, and they take no part in electricity generation in a Si PV cell.
But high photon energy offers little advantage in current generation. In the process of pair creation the photon disappears. 1.14 eV of its energy has gone to “knocking out” the electron from the covalent bond – and what happens to the remaining energy? Well, it’s converted into kinetic energy of the electron and the hole. But what determines the output power of the PV cell is the number of electron-hole pairs produced, not their energy. The extra energy of a pair is quickly lost in collisions with atoms. So, of the 3.1 eV of a violet light photon energy only 1.14 eV does “useful work”, whereas the rest, 1.96 eV or 63% of the the photon energy, is wasted.
What’s described above is not the only factor contributing to lowering the efficiency of PV cell. But we will not discuss the topic any further because the calculation of the maximum theoretical efficiency of a PV cell is a complicated task. The Author would rather refer the the Readers who are specifically interested in the topic to other sources, such as, e.g., this Wikipedia article, and references therein. The Wiki article presents in greater detail the results reported by Shockley and Queisser in a 1961 paper. These authors, trough thorough calculations, determined the theoretical efficiency limit for single np junction1 solar cells made of different materials. For instance, for a silicon cell such as the one discussed in the preceding Section, the Shockley- Queisser theory predicts a maximum possible efficiency of 33.2%.
Practical Efficiency
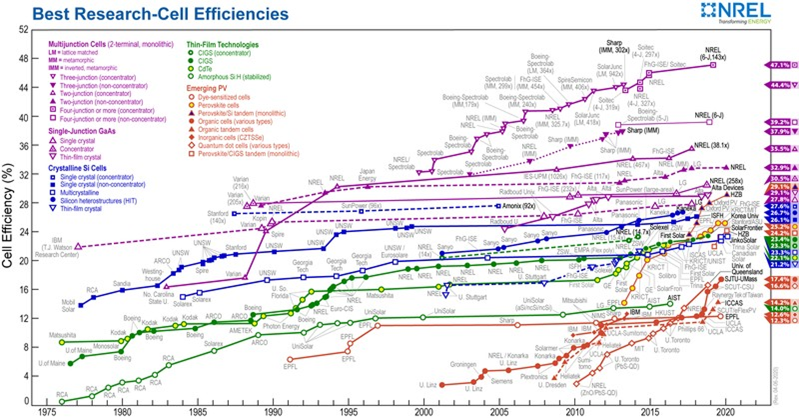
But for ordinary users of PV cells what really matters is the practical efficiency. For the mass-produced Si cells this figure is about 15%. But there is a continuing progress in the field. Competing manufacturers are devoting much effort to get closer to the Shockley-Queisser limit. For more money one can now purchase panels with efficiency over 20%. A list of the most efficient products on the 2018 market is given, e.g., in this Web page. It’s also interesting to watch a graph showing, for the period since 1976, how the efficiency of various types of PV cells improves with the passage of time. The graph, originally published by the National Renewable Energy Laboratory, is presented above as the Fig. \(\PageIndex{1}\)
The plot looks like the proverbial “spaghetti plate”, but it’s worth spending a few minutes to examine different curves. It can be found in many different Web pages which enable the reader to study a blown-up version on the screen – for instance, in this Wiki article (which has already been quoted here) in the section Comparison.
It should be noted that the NREL chart shows the best results obtained in research labs – the efficiency of mass-manufactured products is always lower. However, one can see that the efficiency of single crystal Si cells – the most popular type today – in some research was as high as over 27%. One can therefore expect that an efficiency over 20% may soon become a standard for mass-produced PV panels.
In this Chapter, we have not mention yet some new emerging technologies, such as organic PV cells, or cells made of semiconductors of perovskite structure. Such materials may offer a substantial reduction of manufacturing costs. The new emerging technologies have not yet entered the market – but, in the future, who knows? So, for those of you who are interested in solar power and think of becoming a solar power user in the future, it is recommended to observe the news related to news related to new technologies of harnessing solar energy.
Going back to efficiency: it should be noted that efficiency is not always a critical factor. If a PV panel generates an amount of power that does not satisfy its owner, one possible solution of the problem may be replacing the panel with one of a higher efficiency. But a simpler (and probably a cheaper) solution may be adding more panels of the same type.
There is a clear practical difference between the efficiency of a thermal engine, and the efficiency of a solar PV panel. Consider a conventional coal- burning power plant. The efficiency of an average facility of such kind is about 30%. It means that if the plant uses, say, 100 tons of coal, only the energy released by burning 30 tons of coal is converted to electric energy – and the energy released by burning 70 tons of coal is wasted (it is spent mostly for heating river water or ambient air in the cooling system, as required by the Second Law of Thermodynamics). However, one needs to pay not only for those “good” 30 tons, but also for the 70 tons from which the energy is wasted, and nothing can be done to prevent it.
In the case of solar power things look slightly different. If, say, 15% of solar power is converted to usable energy, 85% is wasted, right? But almost all solar power reaching the Earth surface is “wasted” in a similar way! Nobody needs to pay for that 85% of solar power which is “wasted” due to the not-very-high conversion efficiency of a solar cell! It’s all for free! Not enough power? Just add more panels! Well, this is not for free, but it is a one-time investment. After the period of amortization – which is not very long at the current prices – there will be no need to pay for the power, the “usable” as well for the “wasted”.
___________________________________________________
1. By using sophisticate techniques, it is possible to prepare PV cells in which solar light passes through more than one np junction – each made of a different semiconductor material. Such “multilayered” PV cells may attain practical efficiency as high as 46%. They are very expensive, so they are used mostly when there is a “dramatic need” for power – e.g., in the Skylab, or in spacecrafts sent to distant planets in the Solar System.

