3.3.5: P-N Junction, Part II

Last updated
Save as PDF

Page ID: 89950

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

If you look closely at these pictures, you will notice something. As we remove more and more electrons and holes, we are starting to "uncover" the fixed charges associated with the donors and acceptors. We are making what is known as a depletion region, so named because it is depleted of mobile carriers (holes and electrons). The uncovered net charge in the depletion region is separated, with negative charge in the p-region, and positive charge in the n-region. What will such a charge separation give rise to? Why, an electric field! Of course! Which way will the field point? The electric field which arises from a separation of charges always goes from the positive charge, towards the negative charge. This is shown in Figure \(\PageIndex{1}\).

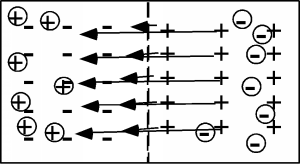
The spatial schematic of the p-n junction as recombination occurs, with an electric field pointing from the fixed positive charges to the fixed negative charges. — Figure \(\PageIndex{1}\): The p-n junction with the resultant built-in electric field

What effect will this field have on our device? It will have the tendency to push the holes back into the p-region and the electrons into the n-region. This is just what we need to counteract the recombination which has been going on, and hopefully bring it to a stop.

Now try to think through what effect this field could have on our energy band diagram. The band diagram is for electrons, so if an electron moves from the right hand side of the device (the n-region) towards the left hand side (the p-region), it will have to move through an electric field which is opposing its motion. But our band diagram had a sudden shift, or discontinuity, in the conduction and valence bands. A moving electron can't suddenly change kinetic energy, the bands must be continuous across the pn junction. We can fix this by making a smoother connection between the two bands (finding the exact function is for a later course).

The electron has do some work, or in other words, the potential energy for the electron must go up; there is a shift in potential energy as electrons move from right to left across the junction.

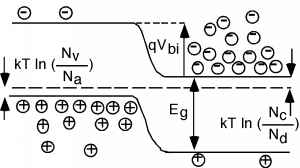
Energy band diagram for a p-n junction at equilibrium, with the electrons in the p-type section occupying a higher energy level than those in the n-type section. The positive charges in the n-type section occupy a lower energy level than those in the p-type section. — Figure \(\PageIndex{2}\): Energy band diagram for a p-n junction at equilibrium

The shift of the bands, which is just the difference between the location of the Fermi level in the n-region and the Fermi level in the p-region, is called the built-in potential, \(V_{\mathrm{BI}}\). This built-in potential keeps the majority of holes in the p-region, and the electrons in the n-region. It provides a potential barrier, which prevents current flow across the junction. (On the band diagram we have to multiply the built-in potential \(V_{\mathrm{BI}}\) by the charge of an electron, \(q\), so that we can represent the shift in energy in terms of electron volts, the unit of potential energy used in band diagrams.)

How big is \(V_{bi}\)? This is not too hard to figure out. Let's look at Figure \(\PageIndex{2}\) a little more carefully. Remember, we know from Equation \(1.3.7\) that since \(n=N_{d}\) in the n-region and \(p=N_{a}\) in the p-region, we can relate the distance of the Fermi level from \(E_{c}\) and \(E_{f}\) by \[E_{c} - E_{f} = kT \ln \left( \frac{N_{c}}{N_{d}}\right) \nonumber \] and \[E_{f}-E_{v} = kT \ln \left(\frac{N_{v}}{N_{a}}\right) \nonumber \] Look at Figure \(\PageIndex{2}\) and see if you can agree that \[\begin{array}{l} qV_{\mathrm{BI}} &= \ E_{g} - \left(E_{c}-E_{f}\right) - \left(E_{f}-E_{v}\right) \\ &= \ E_{g}-kT \ln \left(\frac{N_{c}}{N_{d}}\right) - kT \ln \left(\frac{N_{c}}{N_{d}}\right) \\ &= \ E_{g} - kT \ln \left(\frac{N_{c} N_{v}}{N_{d} N_{a}}\right) \end{array} \nonumber \]

where the \(N_{d}\) and \(N_{a}\) are the doping densities in the n and p regions respectively. Remember that \(kT=1/40 \mathrm{~eV} = 0.025 \mathrm{~eV}\), \(E_{g} = 1.1 \mathrm{~eV}\), and \(N_{c}\) and \(N_{v}\) are both \(\approx \left(10^{19}\right)\). Thus, \[q V_{\mathrm{BI}} = 1.1 \mathrm{~eV} - 0.025 \mathrm{~eV} \cdot \ln \left(\frac{10^{38}}{N_{d} N_{a}}\right) \nonumber \]

Here the \(q\) in front of the \(V_{\mathrm{BI}}\) and the \(e\) in \(\mathrm{eV}\) are both the charge of 1 electron, and they cancel out, making \[V_{\mathrm{BI}} = \left(1.1 - 0.025 \ln \left(\frac{10^{38}}{N_{d} N_{a}}\right) \right) \mathrm{~volts} \nonumber \]

Suppose both \(N_{d}\) and \(N_{a}\) are both about \(10^{15}\) — not uncommon values. How big would the built-in potential be in this case?