3.6.1: Tables of geometries
- Page ID
- 656
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
The following tables present several moment of inertias of commonly used geometries.
Table 3.1 Moments of Inertia for various plane surfaces about their center of gravity (full shapes).
| Shape Name | Picture Description | \(\mathbf{x_c}\), \(\mathbf{x_c}\) | \(\mathbf{A}\) | \(\mathbf{I_{xx}}\) |
| Rectangle | 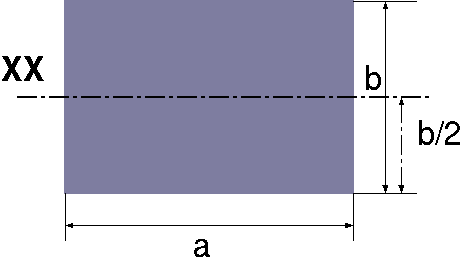 |
\(\dfrac{a}{2}\,;\dfrac{b}{2}\) | \(a\,b\) | \(\dfrac{a\,b^{3}}{12}\) |
| Triangle | 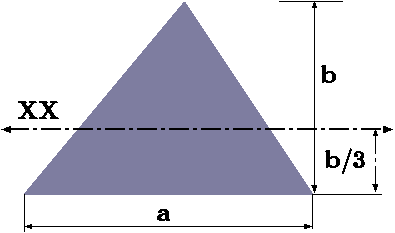 |
\(\dfrac{a}{3}\) | \(\dfrac{a\,b}{3}\) | \(\dfrac{a\,b^{3}}{36}\) |
| Circle | 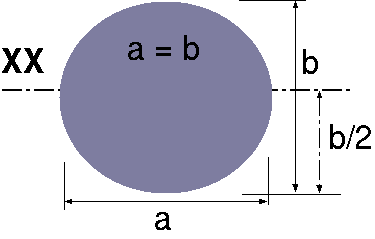 |
\(\dfrac{b}{2}\) | \(\dfrac{\pi\, b^2}{4}\) | \(\dfrac{\pi b^4}{64}\) |
| Ellipse | 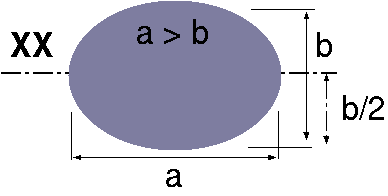 |
\(\dfrac{a}{2}\; \dfrac{b}{2}\) | \(\dfrac{\pi\, ab}{4}\) | \(\dfrac{ab^2}{64}\) |
| \(y=\alpha\,x^2\) Parabola |
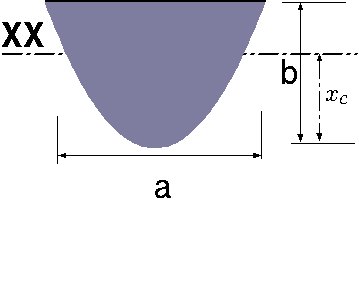 |
\(\dfrac{3\,\alpha\,b}{15\,\alpha-5}\) | \(\dfrac{6\alpha -2}{3} \, \left( \dfrac{b}{\alpha}\right)^{\dfrac{3}{2}}\) | \(\dfrac{\sqrt{b}\,\left( 20\,{b}^{3}-14\,{b}^{2}\right) }{35\,\sqrt{\alpha}}\) |
| Quadrant of Circle |
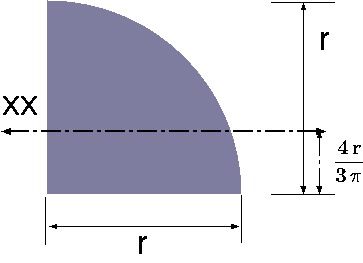 |
\(\dfrac{4\,r}{3\,\pi}\) | \(\dfrac{\pi\,r^2}{4}\) | \(r^4\left(\dfrac{\pi}{16} - \dfrac{4}{9\pi}\right)\) |
| Ellipsoidal Quadrant |
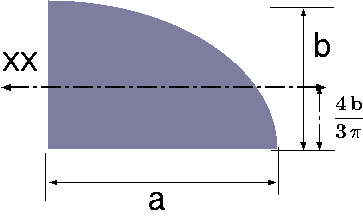 |
\(\dfrac{4\,b}{3\,\pi}\) | \(\dfrac{\pi\,a\,b}{4}\) | \(a\,b^3\left(\dfrac{\pi}{16} - \dfrac{4}{9\pi}\right)\) |
| half of of Ellipse |
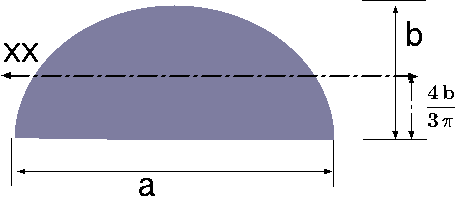 |
\(\dfrac{4\,b}{3\,\pi}\) | \(\dfrac{\pi\,a\,b}{4}\) | \(a\,b^3\left(\dfrac{\pi}{16} - \dfrac{4}{9\pi}\right)\) |
| Circular Sector |
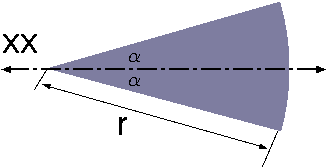 |
\(0\) | \(2{\alpha}\,r^2\) | \(\dfrac{r^4}{4} \left(\alpha - \dfrac{1}{2}\sin2\alpha\right)\) |
| Circular Sector |
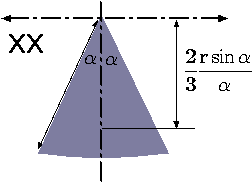 |
\(\dfrac{2}{3}\dfrac{r\,\sin\alpha}{\alpha}\) | \(2{\alpha}\,r^2\) |
\(I_{x^{'}x^{'}} =\)\(\dfrac{r^4}{4} \left(\alpha + \dfrac{1}{2}\sin2\alpha\right)\) |
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


