2. Radiative (Band-to-Band) Recombination

Last updated
Save as PDF

Page ID: 5963

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Radiative recombination is, as it sounds, the reverse process of photon absorption, where an electron drops back down to its equilibrium energy band and radiates a photon. The photon emitted may have the energy of the band gap difference or less, depending on how much energy is lost in the mechanism (due to such interactions as phonon emission in indirect semiconductors). Furthermore, radiative recombination plays a more major role in direct band semiconductors, where the direct recombination does not involve as many steps, however the role of radiative recombination is still minor for most solar applications¹.

It is worth noting that the mechanism by which charge carriers recombine is a factor that determines the lifetime of the charge carrier; just as for direct band gap absorption, direct radiative recombination has shorter carrier lifetimes than indirect radiative recombination, which involves more interactions (such as with phonons)¹. This factor of how long charge carriers survive before recombination is important and comes into play when discussing the ability for charge carriers to contribute to current flow.

The total radiative recombination rate, given below as R, is proportional to the product of the concentration of occupied states (electrons, n) in the conduction band and that of the unoccupied states in the valence band (holes, p):

where B is a constant for a given semiconductor that can actually be calculated from the semiconductor’s absorption coefficient (due to the relationship between optical absorption and the recombination process)².

In thermal equilibrium, the recombination rate is balanced by an equal and opposite generation rate, and so without any extra stimulus to generate free charge carriers above equilibrium, we have that the net equilibrium recombination rate U is given by the total recombination rate minus the equilibrium generation rate²:

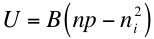
where n_i² is the familiar “intrinsic carrier concentration” and the other variables are the same as the previous equation.

References

1. Goetzberger, Adolf et.al. Crystalline Silicon Solar Cells. Chichester: John Wiley & Sons Ltd., 1998.

2. Green, Martin A. Solar Cells: Operating Principles, Technology, and System Applications. Englewood Cliffs: Prentice-Hall, Inc., 1982. Full book ordering information at www.pv.unsw.edu.au.