6.15: Frequency Shift Keying
- Page ID
- 1867
- Frequency Shift Keying uses the bit to affect the frequency of a carrier sinusoid.
In frequency-shift keying (FSK), the bit affects the frequency of a carrier sinusoid.
\[s_{0}(t)=A_{P_{T}}(t)\sin (2\pi f_{0}t) \nonumber \]
\[s_{1}(t)=A_{P_{T}}(t)\sin (2\pi f_{1}t) \nonumber \]
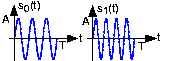
The frequencies \(f_0\), \(f_1\) are usually harmonically related to the bit interval. In the depicted example,
\[f_{0}=\frac{3}{T}\; and\; f_{1}=\frac{4}{T} \nonumber \]
As can be seen from the transmitted signal for our example bit stream (Figure 6.15.2) the transitions at bit interval boundaries are smoother than those of BPSK.
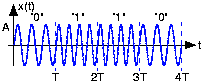
To determine the bandwidth required by this signal set, we again consider the alternating bit stream. Think of it as two signals added together: The first comprised of the signal \(s_0(t)\), the zero signal, \(s_0(t)\), zero, etc., and the second having the same structure but interleaved with the first and containing \(s_1(t)\) (Figure 6.15.3).
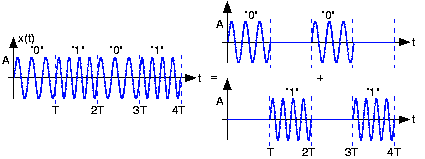
Each component can be thought of as a fixed-frequency sinusoid multiplied by a square wave of period \(2T\) that alternates between one and zero. This baseband square wave has the same Fourier spectrum as our BPSK example, but with the addition of the constant term \(c_0\). This quantity's presence changes the number of Fourier series terms required for the 90% bandwidth: Now we need only include the zero and first harmonics to achieve it. The bandwidth thus equals, with \(f_0 < f_1\).
\[f_{1}+\frac{1}{2T}-\left ( f_{0}-\frac{1}{2T} \right )=f_{1}-f_{0}+\frac{1}{T} \nonumber \]
If the two frequencies are harmonics of the bit-interval duration,
\[f_{0}=\frac{k_{0}}{T}\; and\; f_{1}=\frac{k_{1}}{T} \nonumber \]
with \(k_1 > k_0\), the bandwidth equals
\[\frac{k_{1}+-k_{0}+1}{T} \nonumber \]
If the difference between harmonic numbers is 1, then the FSK bandwidth is smaller than the BPSK bandwidth. If the difference is 2, the bandwidths are equal and larger differences produce a transmission bandwidth larger than that resulting from using a BPSK signal set.


