2.4: How to Prove Security with The Hybrid Technique

We proved that one-time pad satisfies the uniform ciphertexts property (Claim 1.3) by carefully calculating certain probabilities. This will not be a sustainable strategy as things get more complicated later in the course. In this section we will introduce a technique for proving security properties, which usually avoids tedious probability calculations.

Chaining Several Components

Before getting to a security proof, we introduce a convenient lemma. Consider a compound program like \(\mathcal{A} \diamond \mathcal{L}_{1} \diamond \mathcal{L}_{2}\). Our convention is that subroutine calls only happen from left to right across the \(\diamond\) symbol, so in this example, \(\mathcal{L}_{1}\) can make calls to subroutines in \(\mathcal{L}_{2}\), but not vice-versa. Depending on the context, it can sometimes be convenient to interpret \(\mathcal{A} \diamond \mathcal{L}_{1} \diamond \mathcal{L}_{2}\) as:

• \(\left(\mathcal{A} \diamond \mathcal{L}_{1}\right) \diamond \mathcal{L}_{2}\) : a compound calling program linked to \(\mathcal{L}_{2}\). After all, \(\mathcal{A} \diamond \mathcal{L}_{1}\) is a program that makes calls to the interface of \(\mathcal{L}_{2}\).
• or: \(\mathcal{A} \diamond\left(\mathcal{L}_{1} \diamond \mathcal{L}_{2}\right): \mathcal{A}\) linked to a compound library. After all, \(\mathcal{A}\) is a program that makes calls to the interface of \(\left(\mathcal{L}_{1} \diamond \mathcal{L}_{2}\right)\)

The placement of the parentheses does not affect the functionality of the overall program, just like how splitting up a real program into different source files doesn’t affect its functionality. In fact, every security proof in this book will have some intermediate steps that involve compound libraries. We will make heavy use of the following helpful result:

Lemma 2.11 (Chaining)

If \(\mathcal{L}_{\text {left }} \equiv \mathcal{L}_{\text {right }}\) then, for any library \(\mathcal{L}^{*}\), we have \(\mathcal{L}^{*} \diamond \mathcal{L}_{\text {left }} \equiv \mathcal{L}^{*} \diamond \mathcal{L}_{\text {right }}\).

Proof

Note that we are comparing \(\mathcal{L}^{*} \diamond \mathcal{L}_{\text {left }}\) and \(\mathcal{L}^{*} \diamond \mathcal{L}_{\text {right }}\) as compound libraries. Hence we consider a calling program \(\mathcal{A}\) that is linked to either \(\mathcal{L}^{*} \diamond \mathcal{L}_{\text {left }}\) or \(\mathcal{L}^{*} \diamond \mathcal{L}_{\text {right }}\).

Let \(\mathcal{A}\) be such an arbitrary calling program. We must show that \(\mathcal{A} \diamond\left(\mathcal{L}^{*} \diamond \mathcal{L}_{\text {left }}\right)\) and \(\mathcal{A} \diamond\left(\mathcal{L}^{*} \diamond \mathcal{L}_{\text {right }}\right)\) have identical output distributions. As mentioned above, we can interpret \(\mathcal{A} \diamond \mathcal{L}^{*} \diamond \mathcal{L}_{\text {left }}\) as a calling program \(\mathcal{A}\) linked to the library \(\mathcal{L}^{*} \diamond \mathcal{L}_{\text {left }}\), but also as a calling program \(\mathcal{A} \diamond \mathcal{L}^{*}\) linked to the library \(\mathcal{L}_{\text {left. }}\). Since \(\mathcal{L}_{\text {left }} \equiv \mathcal{L}_{\text {right, }}\), swapping \(\mathcal{L}_{\text {left for }} \mathcal{L}_{\text {right }}\) has no effect on the output of any calling program. In particular, it has no effect when the calling program happens to be the compound program \(\mathcal{A} \diamond \mathcal{L}^{*}\). Hence we have:

Since \(\mathcal{A}\) was arbitrary, we have proved the lemma.

An Example Hybrid Proof

In this section we will prove something about the following scheme, which encrypts twice with OTP, using independent keys:

Construction 2.12 ("Double OTP")

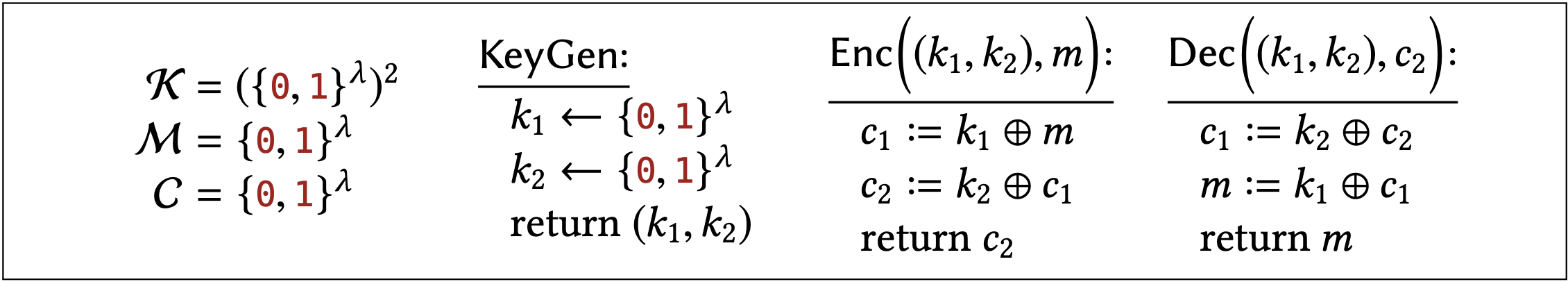
It would not be too hard to directly show that ciphertexts in this scheme are uniformly distributed, as we did for plain OTP. However, the new hybrid technique will allow us to leverage what we already know about OTP in an elegant way, and avoid any probability calculations.

Claim 2.13

Construction 2.12 has one-time uniform ciphertexts (Definition 2.6).

Proof

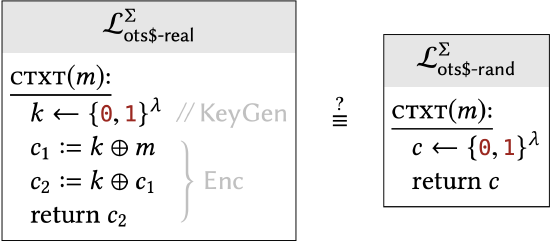
In terms of libraries, we must show that:

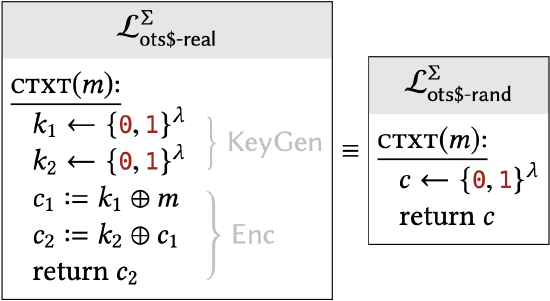
Instead of directly comparing these two libraries, we will introduce some additional libraries \(\mathcal{L}_{\text {hyb }-1}, \mathcal{L}_{\text {hyb-2 }}, \mathcal{L}_{\text {hyb-3 }}\), and show that:

\[\mathcal{L}_{\text {ots\$-real }}^{\Sigma} \equiv \mathcal{L}_{\text {hyb-1 }} \equiv \mathcal{L}_{\text {hyb-2 }} \equiv \mathcal{L}_{\text {hyb-3 }} \equiv \mathcal{L}_{\text {ots\$-rand }}^{\Sigma}\]

Since the \(\equiv\) symbol is transitive, this will achieve our goal.

The intermediate libraries are called hybrids, since they will contain a mix of characteristics from the two "endpoints" of this sequence. These hybrids are chosen so that it is very easy to show that consecutive libraries in this sequence are interchangeable. The particular hybrids we have in mind here are:

Next, we provide a justification for each "\(\equiv\)" in the expression above. For each pair of adjacent libraries, we highlight their differences below:

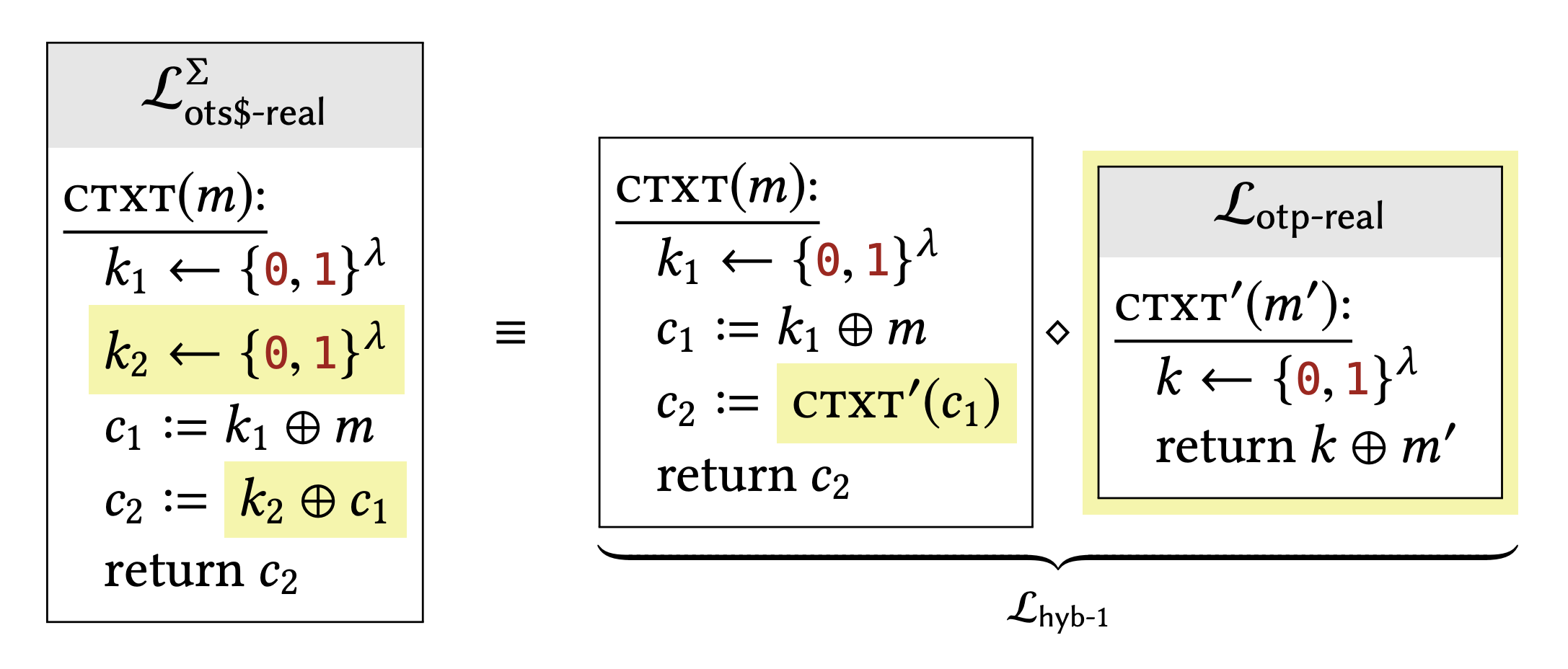
The only difference between these two libraries is that the highlighted expressions have been factored out into a separate subroutine, and some variables have been renamed. In both libraries, \(c_{2}\) is chosen as the xOR of \(c_{1}\) and a uniformly chosen string. These differences make no effect on the calling program. Importantly, the subroutine that we have factored out is exactly the one in the \(\mathcal{L}_{\text {otp-real }}\) library (apart from renaming the subroutine).

Claim 2.7 says that \(\mathcal{L}_{\text {otp-real }} \equiv \mathcal{L}_{\text {otp-rand }}\), so Lemma \(2.11\) says that we can replace an instance of \(\mathcal{L}_{\text {otp-real }}\) in a compound library with \(\mathcal{L}_{\text {otp-rand, as we have done here. This change will }}\) have no effect on the calling program.

The only difference between these two libraries is that a subroutine call has been inlined. This difference has no effect on the calling program.

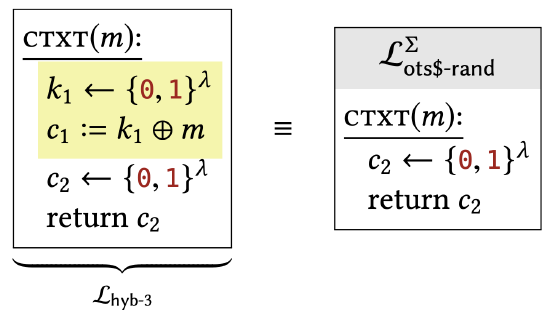
The only difference between these two libraries is that the two highlighted lines have been removed. But it should be clear that these lines have no effect: \(k_{1}\) is used only to compute \(c_{1}\), which is never used again. Hence, this difference has no effect on the calling program.

The final hybrid is exactly \(\mathcal{L}_{\text {ots\$-rand }}^{\Sigma}\) (although with a variable name changed). We have shown that \(\mathcal{L}_{\text {ots\$-rand }}^{\Sigma} \equiv \mathcal{L}_{\text {ots\$-real }}^{\Sigma}\), meaning that this encryption scheme has one-time uniform ciphertexts.

Summary of the Hybrid Technique

We have now seen our first example of the hybrid technique for security proofs. All security proofs in this book use this technique.

• Proving security means showing that two particular libraries, say \(\mathcal{L}_{\text {left }}\) and \(\mathcal{L}_{\text {right }}\), are interchangeable.
• Often \(\mathcal{L}_{\text {left and }} \mathcal{L}_{\text {right }}\) are significantly different, making them hard to compare directly. To make the comparison more manageable, we can show a sequence of hybrid libraries, beginning with \(\mathcal{L}_{\text {left }}\) and ending with \(\mathcal{L}_{\text {right }}\). The idea is to break up the large "gap" between \(\mathcal{L}_{\text {left }}\) and \(\mathcal{L}_{\text {right }}\) into smaller ones that are easier to justify.
• It is helpful to think of "starting" at \(\mathcal{L}_{\text {left, }}\) and then making a sequence of small modifications to it, with the goal of eventually reaching \(\mathcal{L}_{\text {right. }}\). You must justify why each modification doesn’t affect the calling program (i.e., why the two libraries before/after your modification are interchangeable).
• As discussed in Section 2.2, simple things like inlining/factoring out subroutines, changing unused variables, changing unreachable statements, or unrolling loops are always "allowable" modifications in a hybrid proof since they have no effect on the calling program. As we progress in the course, we will see more kinds of useful modifications.

A Contrasting Example

Usually the boundary between secure and insecure is razor thin. Let’s make a small change to the previous encryption scheme to illustrate this point. Instead of applying OTP to the plaintext twice, with independent keys, what would happen if we use the same key?

Construction \(2.14\) \((" \mathrm{dOuB} \ell \exists \mathrm{OTP})\)

You probably noticed that the ciphertext \(c_{2}\) is computed as \(c_{2}:=k \oplus(k \oplus m)\), which is just a fancy way of saying \(c_{2}:=m\). There is certainly no way this kind of "double-OTP" is secure.

For educational purposes, let’s try to repeat the steps of our previous security proof on this (insecure) scheme and see where things break down. If we wanted to show that Construction \(2.14\) has uniform ciphertexts, we would have to show that the following two libraries are interchangeable:

Figure \(\PageIndex{1}\): Copy and Paste Caption here. (Copyright; author via source)

In the previous hybrid proof, the first step was to factor out the statements " \(k_{2} \leftarrow\{0,1\}^{\lambda}\); \(c_{2}:=k_{2} \oplus c_{1} "\) into a separate subroutine, so we could argue that the result of \(c_{2}\) was uniformly distributed. If we do something analogous with this example, we get:

Do you see the problem? In " \(\mathcal{L}_{\mathrm{hyb}}\) ", we have tried to move the variable \(k\) into \(\mathcal{L}_{\text {otp-real }}\). Since this scope is private, every operation we want to do with \(k\) has to be provided by its container library \(\mathcal{L}_{\text {otp-real }}\). But there is a mismatch: \(\mathcal{L}_{\text {otp-real }}\) only gives us a way to use \(k\) in one XOR expression, whereas we need to use the same \(k\) in two XOR expressions to match the behavior of \(\mathcal{L}_{\text {ots\$-real }}\). The compound library \(\mathcal{L}_{\text {hyb }}\) has an unresolved reference to \(k\) in the line " \(c_{1}:=k \oplus m\)," and therefore doesn’t have the same behavior as \(\mathcal{L}_{\text {ots\$-real. }}{ }^{4}\) This is the step of the security proof that breaks down.

Here’s a more conceptual way to understand what went wrong here. The important property of OTP is that its ciphertexts look uniform when the key is used to encrypt only one plaintext. This "double OTP" variant uses OTP in a way that doesn’t fulfill that condition, and therefore provides no security guarantee. The previous (successful) proof was able to factor out some XOR’s in terms of \(\mathcal{L}_{\text {otp-real without breaking anything, and that's how we }}\) know the scheme was using OTP in a way that is consistent with its security guarantee.

As you can hopefully see, the process of a security proof provides a way to catch these kinds of problems. It is very common in a hybrid proof to factor out some statements in terms of a library from some other security definition. This step can only be done successfully if the underlying cryptography is being used in an appropriate way.

---

\({ }^{4}\) I would say that the library "doesn’t compile" due to a scope/reference error.