2.4: The Euler and De Moivre Identities
- Page ID
- 9957
The Euler and De Moivre identities are the fundamental identities for deriving trigonometric formulas. From the identity \(e^{jθ}=\cosθ+j\sinθ\) and the conjugate identity \(e^{−jθ}=(e^{jθ})^∗=\cosθ−j\sinθ\), we have the Euler identities for \(\cosθ\) and \(\sinθ\):
\[\cosθ=\frac {e^{jθ}+e^{−jθ}} {2} \nonumber \]
\[\sinθ=\frac {e^{jθ}−e^{−jθ}} {2j} \nonumber \]
These identities are illustrated in the Figure.
The identity \(e^{jθ}=\cosθ+j\sinθ\) also produces the De Moivre identity:
\[(\cosθ+j\sinθ)n=(e^{jθ})^n=e^{jnθ}=\cos nθ+j\sin nθ \nonumber \]
When the left-hand side of this equation is expanded with the binomial expansion, we obtain the identity
\[∑_{k=0}^n \begin{pmatrix}n\\k\end{pmatrix} (cosθ)n−k(jsinθ)k=cosnθ+jsinnθ \nonumber \]
Binomial Coefficients and Pascal's Triangle
The binomial coefficients (nk) in Equation are shorthand for the number
\[\begin{pmatrix}n\\k\end{pmatrix}=n!(n−k)!k!'k=0,1,...,n \nonumber \]
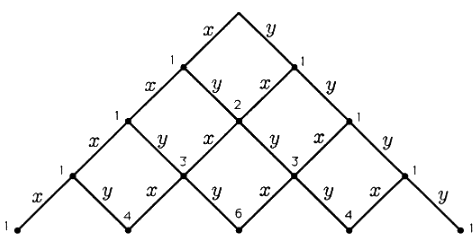
This number gives the coefficient of \(x^{n−k}y^k\) in the expansion of \((x+y)^n\). How do we know that there are \(\begin {pmatrix} n\\k\end {pmatrix}\) terms of the form \(x^{n−k}y^k\)? One way to answer this question is to use Pascal's triangle, illustrated in Figure. Each node on Pascal's triangle shows the number of routes that terminate at that node. This number is always the sum of the number of routes that terminate at the nodes just above the node in question. If we think of a left-hand path as an occurrence of an x and a right-hand path as an occurrence of a y, then we see that Pascal's triangle keeps track of the number of occurrences of \(x^{n−k}y^k\).
Prove \(\begin{pmatrix}n\\k\end{pmatrix}=(n^{n−k})\).
Find an identity for \(\begin{pmatrix}n−1\\k−1\end{pmatrix}+\begin{pmatrix}k\\n−1)\end{pmatrix}\).
Find “half-angle” formulas for \(\cos2θ\) and \(\sin2θ\).
Show that
- \(\cos3θ=\cos^2θ−3 \cosθ\sin2θ\)
- \(\sin3θ=34\cos^2θ \sinθ−\sin3θ\)


