5.4: Composition of Transformations

Often we will want to perform several operations on an object before we display the result. For example, suppose we want to rotate by \(\frac{\pi}{3}\) and reduce to \(\frac{1}{2}\) size in each dimension:

\[\mathrm{G}_{1}=\mathrm{R}\left(\frac{\pi}{3}\right) \mathrm{G} \nonumber \]

\[\mathrm{G}_{\text {new }}=\mathrm{S}\left(\frac{1}{2}, \frac{1}{2}\right) \mathrm{G}_{1} \nonumber \]

If there are \(n\) points in the matrix \(G\), it will require \(4n\) multiplications to perform each of these operations, for a total of \(8n\) multiplications. However, we can save some multiplications by noting that

\[\mathrm{G}_{\text {new }}=\mathrm{S}\left(\frac{1}{2}, \frac{1}{2}\right)\left[\mathrm{R}\left(\frac{\pi}{3}\right) \mathrm{G}\right]=\mathrm{AG} \nonumber \]

where

\[\begin{align}
\mathrm{A} &=\mathrm{S}\left(\frac{1}{2}, \frac{1}{2}\right) \mathrm{R}\left(\frac{\pi}{3}\right) \nonumber \\
&=\left[\begin{array}{ll}
\frac{1}{2} \cos \left(\frac{\pi}{3}\right) & -\frac{1}{2} \sin \left(\frac{\pi}{3}\right) \\
\frac{1}{2} \sin \left(\frac{\pi}{3}\right) & \frac{1}{2} \cos \left(\frac{\pi}{3}\right)
\end{array}\right]
\end{align} \nonumber \]

In other words, we take advantage of the fact that matrix multiplication is associative to combine \(S\) and \(R\) into a single operation \(A\), which requires only 8 multiplications. Then we operate on \(G\) with \(A\), which requires \(4n\) multiplications. By “composing” the two operations, we have reduced the total from \(8n\) to \(4n+8\) multiplications. Furthermore, we can now build operators with complex actions by combining simple actions.

Example \(\PageIndex{1}\)

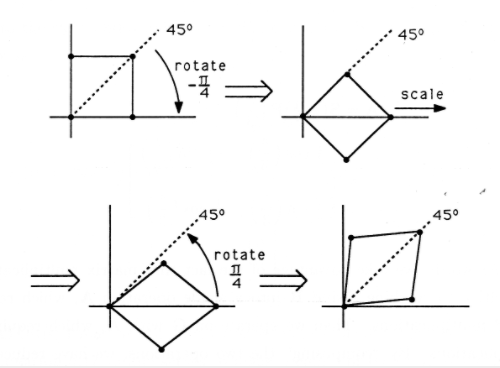
We can build an operator that stretches objects along a diagonal line by composing scaling and rotation. We must

1. rotate the diagonal line to the x-axis with R\((−\theta)\);
2. scale with S\((s,1)\); and
3. rotate back to the original orientation with R(\(\theta\))

Figure 1 shows a square being stretched along a \(45^{\circ}\) line. The composite operator that performs this directional stretching is

\[\begin{align}
\mathrm{A}(\theta, s) &=\operatorname{R}(\theta) \mathrm{S}(s, 1) \mathrm{R}(-\theta) \nonumber \\
&=\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\left[\begin{array}{ll}
s & 0 \\
0 & 1
\end{array}\right]\left[\begin{array}{ll}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right] \nonumber \\
&=\left[\begin{array}{ll}
s \cos ^{2} \theta+\sin ^{2} \theta & (s-1) \sin \theta \cos \theta \\
(s-1) \sin \theta \cos \theta & \cos ^{2} \theta+s \sin ^{2} \theta
\end{array}\right] .
\end{align} \nonumber \]

Note that the rightmost operator in a product of operators is applied first.

Figure \(\PageIndex{1}\): Rotating and Scaling for Directional Stretching