6.4: Moving Averages
- Page ID
- 9985
Moving averages are generalizations of weighted averages. They are designed to “run along an input sequence, computing weighted averages as they go.” A typical moving average over \(N\) inputs takes the form
\[\begin{align}
x_{n} &=\qquad \qquad \qquad \sum_{k=0}^{N-1} w_{k} u_{n-k} \nonumber\\
&=w_{0} u_{n}+w_{1} u_{n-1}+\cdots+w_{N-1} u_{n-(N-1)}
\end{align} \nonumber \]
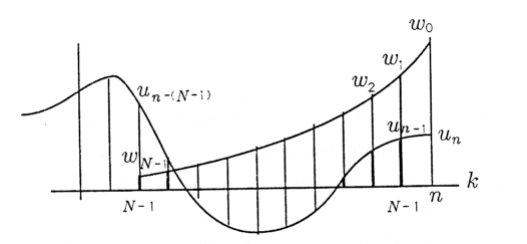
The most current input, \(u_n\), is weighted by \(w_0\); the next most current input, \(u_{n-1}\), is weighted by \(w_1\) ; and so on. This weighting is illustrated in Figure 1. The sequence of weights, \(w_0\) through \(w_{N-1}\), is called a “window,” a “weighting sequence,” or a “filter.” In the example illustrated in Figure 6.8, the current value \(u_n\) is weighted more heavily than the least current value. This is typical (but not essential) because we usually want \(x_n\) to reflect more of the recent past than the distant past.
When the weights \(w_{0}, w_{1}, \ldots, w_{N-1}\) are all equal to \(\frac{1}{N}\), then the moving average \(x_n\) is a “simple moving average”:
\[x_{n}=\frac{1}{N}\left[u_{n}+u_{n-1}+\cdots+u_{N-1}\right] . \nonumber \]
This is the same as the simple average, but now the simple average moves along the sequence of inputs, averaging the \(N\) most current values.
Evaluate the moving average \(x_{n}=\sum_{k=0}^{N-1} \frac{1}{N} u_{n-k}\) for the inputs
- \(u_{n}= \begin{cases}0, & n<0 \\ u, & n \geq 0\end{cases}\)
- \(u_{n}= \begin{cases}0, & n \leq 0 \\ n, & n>0\end{cases}\)
Interpret your findings.
Evaluate the simple moving average \(x_{n}=\sum_{k=0}^{N-1} \frac{1}{N} u_{n-k}\) when \(u_n\) is the sequence
\(u_{n}= \begin{cases}0, & n<0 \\ a^{n}, & n \geq 0\end{cases}\)
Interpret your result.
When the weights \(w_n\) equal \(w_0a^n\) for \(n=0,1,...,N−1\), then the moving average \(x_n\) takes the form
\[x_{n}=w_{0} \sum_{k=0}^{N-1} a^{k} u_{n-k} . \nonumber \]
When \(a < 1\), then \(u_n\) is weighted more heavily than \(u_{n−(N−1)}\); when \(a>1\), \(u_{n−(N−1)}\) is weighted more heavily than \(u_n\); when \(a=1\), \(u_n\) is weighted the same as \(u_{n−(N−1)}\).
Evaluate \(w_0\) so that the exponential weighting sequence \(w_{n}=w_{0} a^{n}(n=0,1, \ldots, N-1)\) is a valid window (i.e., \(\sum_{n=0}^{N-1} w_{n}=1\)).
Compute the moving average \(x_{n}=\sum_{k=0}^{N-1} w_{0} a^{k} u_{n-k}\) when the input sequence \(u_n\) is
\(u_{n}= \begin{cases}b^{n}, & n \geq 0 \\ 0, & n<0\end{cases}\)
What happens when \(b=a?\) Can you explain this?


