1.3: Exercise
- Page ID
- 86437
Exercises
The one-time pad encryption of plaintext mario (when converted from \(\texttt{ASCII}\) to binary in the standard way) under key \(k\) is:
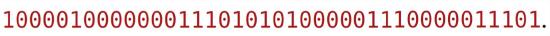
What is the one-time pad encryption of luigi under the same key?
Alice is using one-time pad and notices that when her key is the all-zeroes string \(k=0^{\lambda}\), then \(\operatorname{Enc}(k, m)=m\) and her message is sent in the clear! To avoid this problem, she decides to modify KeyGen to exclude the all-zeroes key. She modifies KeyGen to choose a key uniformly from \(\{0,1\}^{\lambda} \backslash\left\{0^{\lambda}\right\}\), the set of all \(\lambda\)-bit strings except \(0^{\lambda}\). In this way, she guarantees that her plaintext is never sent in the clear.
Is it still true that the eavesdropper’s ciphertext distribution is uniformly distributed on \(\{0,1\}^{\lambda} ?\) Justify your answer.
When Alice encrypts the key \(k\) itself using one-time pad, the ciphertext will always be the all-zeroes string! So if an eavesdropper sees the all-zeroes ciphertext, she learns that Alice encrypted the key itself. Does this contradict Claim \(1.3\) ? Why or why not?
What is so special about defining OTP using the XOR operation? Suppose we use the bitwise-AND operation (which we will write as ’ \(\&\) ’) and define a variant of OTP as follows:

Is this still a good choice for encryption? Why / why not?
Describe the flaw in this argument:
Consider the following attack against one-time pad: upon seeing a ciphertext \(c\), the eavesdropper tries every candidate key \(k \in\{0,1\}^{\lambda}\) until she has found the one that was used, at which point she outputs the plaintext \(m\). This contradicts the argument in Section \(1.2\) that the eavesdropper can obtain no information about \(m\) by seeing the ciphertext.
Suppose Alice encrypts two plaintexts \(m\) and \(m^{\prime}\) using one-time pad with the same key \(k\). What information about \(m\) and \(m^{\prime}\) is leaked to an eavesdropper by doing this (assume the eavesdropper knows that Alice has reused \(k)\) ? Be as specific as you can!
You (Eve) have intercepted two ciphertexts:
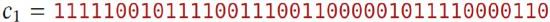
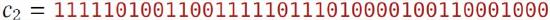
You know that both are OTP ciphertexts, encrypted with the same key. You know that either \(c_{1}\) is an encryption of alpha and \(c_{2}\) is an encryption of bravo or \(c_{1}\) is an encryption of delta and \(c_{2}\) is an encryption of gamma (all converted to binary from Ascir in the standard way)
Which of these two possibilities is correct, and why? What was the key \(k\) ?
A known-plaintext attack refers to a situation where an eavesdropper sees a ciphertext \(c=\operatorname{Enc}(k, m)\) and also learns/knows what plaintext \(m\) was used to generate \(c\).
(a) Show that a known-plaintext attack on OTP results in the attacker learning the key \(k\).
(b) Can OTP be secure if it allows an attacker to recover the encryption key? Is this a contradiction to the security we showed for OTP? Explain.
Suppose we modify the subroutine discussed in Claim \(1.3\) so that it also returns \(k\) :

Is it still true that for every \(m\), the output of EAVESDROP \({ }^{\prime}(m)\) is distributed uniformly in \(\left(\{0,1\}^{\lambda}\right)^{2} ?\) Or is the output distribution different for different choice of \(m\) ?
In this problem we discuss the security of performing one-time pad encryption twice:
(a) Consider the following subroutine that models the result of applying one-time pad encryption with two independent keys:

Show that the output of this subroutine is uniformly distributed in \(\{0,1\}^{\lambda}\).
(b) What security is provided by performing one-time pad encryption twice with the same \(k e y ?\)
We mentioned that one-time pad keys can be used to encrypt only one plaintext, and how this was reflected in the EAVESDROP subroutine of Claim 1.3. Is there a similar restriction about re-using plaintexts in OTP (but with independently random keys for different ciphertexts)? If an eavesdropper knows that the same plaintext is encrypted twice (but doesn’t know what the plaintext is), can she learn anything? Does Claim \(1.3\) have anything to say about a situation where the same plaintext is encrypted more than once?
There is nothing exclusively special about strings and XOR in OTP. We can get the same properties using integers \(\bmod n\) and addition mod \(n\).
This problem considers a variant of one-time pad, in which the keys, plaintexts, and ciphertexts are all elements of \(\mathbb{Z}_{n}\) instead of \(\{0,1\}^{\lambda}\)
(a) What is the decryption algorithm that corresponds to the following encryption algorithm?
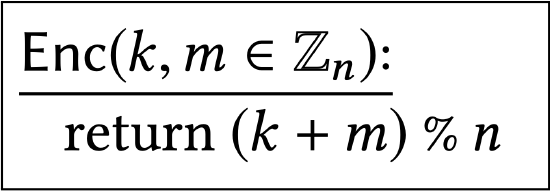
(b) Show that the output of the following subroutine is uniformly distributed in \(\mathbb{Z}_{n}\) :
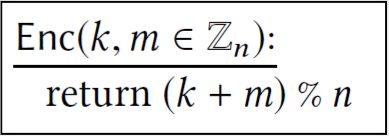
(c) It’s not just the distribution of keys that is important. The way that the key is combined with the plaintext is also important. Show that the output of the following subroutine is not necessarily uniformly distributed in \(\mathbb{Z}_{n}\):



