2.2.1 Metals
- Page ID
- 2758
A few words before you start:
- Conductors in general are a bit boring, whereas conductors in particular applications are often hot topics (take the recent switch from Al to Cu in chip technology, for example).
- There is a large number of highly optimized materials which are used as conductors nowadays. Just enumerating them is tiresome and not very interesting. Still, some knowledge of this issue is a must for materials scientists in the context of electronic materials.
- As far as "theory" goes, there is either not much that goes beyond a basic knowledge of solid state physics (which, it is assumed, you already have), or very involved special theory (e.g. for superconductors or conducting polymers) - for which there is no time.
In conclusion, we will only touch the issue, trying to present all major facets of the topic. In particular, the long list of applications for conductors (much longer than you probably would imagine) will be covered. This chapter, however, will be brief and mostly lists topics and key words.
The Basics
The essential parameters of interest for conductors are:
1. Specific resistivity ρ or specific conductivity σ = 1/ρ.
- The defining "master" equation is
\[\sigma=|q|\cdot n\cdot \mu\]
- With q = magnitude of the charge of the current carrying particles; n = concentration of current carrying particles (usually electrons in conductors) ; µ= mobility of the current carrying particles.
- The units are
\[\left[\rho\right]=\Omega\text{m}\\\left[\sigma\right]=(\Omega\text{m})^{-1}=\text{S/m}\]
- Note that S = "Siemens" = 1/Ω = A/V is a bit old fashioned, but still in use. Note, too, that while the SI standard units call for the meter (m), you will find many values given in Ωcm.
- A homogeneous material with a constant cross-sectional area F and a length lthus has a resistance of R = (ρ · l)/F
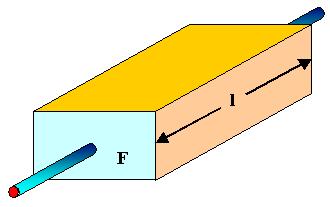
\[R=\frac{\rho\cdot l}{F}\]
- Or, in other words, a cube with 1 cm length has a resistance R given in Ω that is numerically equal to ist specific resistance ρ given in Ωcm.
If electrons are carrying the current, we have q = – e = elementary charge = 1.602 · 10–19 C.
- For units, conversions, and so on consult the link!
2. Ohm's law. Ohm's law (which was not a "law", but an empirical observation) formulated for the specific quantities writes
\[\underline{j}=\sigma\cdot \color{purple}{\underline{E}}\]
- With j = current density (a vector); E = electrical field strength (a vector); σ =specific conductivity, in general a tensor of 2nd rank and, most important, nota function of the field strength E if not specifically noted. In other words, if the specific conductivity of a material is a constant, i.e. a fixed number with respect to E, the material obeys Ohm's law.
- Ohm's law thus means that the E - j characteristics or the easily measured voltage - current characteristics are always straight lines through the origin! Within reasonable values of E, or U, of course.
If you have any problem with these equations, perhaps because you feel Ohm's law should read R = U/I, or if you are not sure about the the meaning of the basic quantities, as e.g., mobility, you have a problem. Turn to the required reading module and other modules accessible from there.
- More about Ohm's law and the failure of classical physics in explaining the conductivity of metals can be found in a second required reading module. Add to this the required reading module for averaging vector quantities and you are ready for this chapter and others to come.
A remark to the mathematical notation: HTML possibilities are limited and it is difficult to adhere to all rules of notation. In case of doubt, clarity and easy reading will have preference to formal correctness. This means:
- Whenever sensible, cursive symbols will be used for variables. It is not sensible, e.g., to use cursive letters for the velocity v, because the cursive v is easily mixed up with the Greek nu ν.
- All equations and the quantities used in equations are always bold - this greatly improves readability. However, it leaves little room for symbolizing vectors by bold lettering, and since underlining is cumbersome and not particularly helpful, we simply will mostly not use special notation for vectors. If you are able to understand this lecture course at all, you will know the vector (or tensor) quantities anyway.
- There are not enough letters in the alphabet to give every physical quantity an unambiguous symbol. One and the same symbol thus traditionally has several meanings, usually quite clear from the context. Occasionally, however, the danger of mix-up occurs. An example in case is the traditional use of the letterE for electrical field strength and for energies (and for Young's modulus in German). While in conventional texts one must give a different letter to these quantities, we will use the advantage of HTML and use color coding whenever the possibility of negative symbol interference raises its ugly head.
The density and mobility of mobile charged carriers thus determines the conductivity.
- The carrier density is a function of bonding (metallic, covalent in semiconductor, etc.), defects (doping in semiconductors) and temperature in general. In metals, however, ne is nearly constant.
- The mobility is a function of collisions between carriers (e.g. electrons and holes) and/or between carriers and obstacles (e.g. phonons and crystal lattice defects).
Carrier concentration and mobility are, in general, hard to calculate from first principles. In semiconductors, the carrier density is easy to obtain, mobility is somewhat harder. In metals, the carrier density is rather fixed, but mobility is quite difficult to calculate, especially for "real" i.e. rather imperfect crystals. There are however, empirical rules or "laws".
- Ohm's "law" asserting that σ is not a function of E but only of some material property that can be expressed as a number.
- Matthiesen's rule, stating that
\[\rho=\rho_\text{Lattice}(T)+\rho_\text{defect}(N)\]
- With N = some measure of defect density.
- A "rule of thumb": ρ is proportional to T for T > some Tcrit
\[\Delta\rho=\alpha_\rho\cdot\rho\cdot\Delta T \approx \frac{0.4\%}{^\circ C}\]
- With Temperature coefficient αρ = 1/ρ · dρ / dT.
- Then we have the Wiedemann-Franz "law", linking electrical conductivity to thermal conductivity, and so on.
The links give some graphs and numbers for representative metals.
Some Values and Comments
The range of resistivity values (at room temperature) for metals is rather limited; here are some values as well as a first and last reminder that σ and ρ, while closely related, are quite different parameters with a numerical value that depends on the choice of the units! Do not mix up cm and m!
| Metal | Ag | Cu | Au | Al | Na | Zn | Ni | Fe | Sn | Pb | Hg |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ [μΩcm] | 1,6 | 1,7 | 2,2 | 2,7 | 4,2 | 5,9 | 6,8 | 9,7 | 12 | 21 | 97 |
| σ = 1/ρ [106 · Ω–1cm–1] |
0.625 | 0.588 | 0,455 | 0.37 | 0.238 | 0.169 | 0.147 | 0.103 | 0.083 | 0.046 | 0.01 |
| σ = 1/ρ [106 · Ω–1m–1] |
62,5 | 58.8 | 45.5 | 37 | 23.8 | 16.9 | 14.7 | 10.3 | 8.3 | 4.6 | 1 |
- The temperature dependence, expressed e.g. in ρ(300K)/ρ(100K) may be a factor of 5 ...10, so it is not a small factor. It may be used and is used, for measuring temperatures, e.g. with well-known Ptresistivity thermometers.
- This is something you should be aware of; cf. the anecdote in the link.
The specific resistivity, however, is not the only property that counts. In selecting a metal, important design parameters might also be:
- Weight, mechanical strength, corrosion resistance, prize, compatibility with other materials, .....
Sometimes it is advisable to look at "figures of merit", i.e. the numerical value coming out of a self-made formula that contains your important criteria in a suitable way.
- One very simple example: Lets say, weight is important. Define a figure of merit = F = ρ/ d, with d = density. The bigger F, the better.
- You now get the following ranking (normalized to FNa = 1):
| Metal | Na | K | Ca | Al | Mg | Cu | Ag |
|---|---|---|---|---|---|---|---|
| F | 1 | 0,77 | 0,69 | 0,56 | 0,52 | 0,28 | 0,25 |
The winner sodium! So you are going to use Sodium - Na for wiring?
- Certainly not. Because now you will either include chemical stability C in your figure of merit (just multiply with C and assign values C = 1 for great stability (e.g. Au, Al,), C = 2 for medium stability (Cu, Mg) and C = 5 for unstable stuff (Na, K, Ca). Or any other number reflecting the importance you put on this parameter. There is no ready made recipe - if precise numbers are not existing, you take your personal grading scale.
- And while you are at it, divide by some price index P. Use the price per kg, or just a rough grade scale.
- In this simple example, you will get a surprising result: No matter what you do, the winner will be Al. It is the (base) material of choice for heavy duty applications when weight matters. In not so simple questions, you really may benefit from using the figure of merit approach.

