2.4.2 Field Enhanced Emission and Tunnelling Effects
- Page ID
- 2770
If you run a cathode, emitting an electron beam, with large electrical fields between the cathode and the anode, you will find that your workfunction EA seems to change to smaller values as the field strength increases.
- This is called Schottky effect; it is observed at large field values of (105 - 108)V/cm.
If you apply even higher field strengths (and remember: E = U/d; you do not need high voltages U, only small dimensions d),EA seems to vanish altogether.
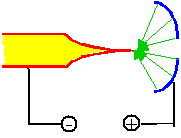
- This effect is is called field emission. It works even at room temperature and is barely temperature dependent, so it can not be a temperature activated process.
- Field emission is rather easy to obtain: all you have to do, is to make a very fine tip with a curvature of the tip in the nm - range as shown on the left.
- Field emission might then occur with a few Volts between the anode and the tip, because all the field lines will have to converge on the small tip.
How can we understand these effects? Whereas the Schottky effect is relatively straight forward, field emission is a manifestation of the tunnelling effect, a purely quantum mechanical phenomenon.
Lets look at how the free electron gas model must be modified at high field strengths - and we will be able to account for both effects.
- The potential energy E outside of the material is such that electrons are to be extracted - it is not constant, but varies with the field strength E simply as
\[E=e \cdot E \cdot x\]
- E, the (constant) applied field strength (written in mauve to make sure that we do not mix it up with the energy E). We have the following situation:
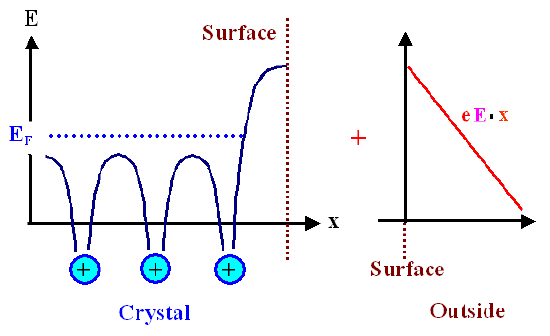
Simply summing up the energies graphically yields the qualitative energy curve for an electron at the edge of a crystal as shown below.
- Whichever way you superimpose the potential energies, the potential barrier to the outside world will always be reduced. This explains qualitatively the Schottky effect.
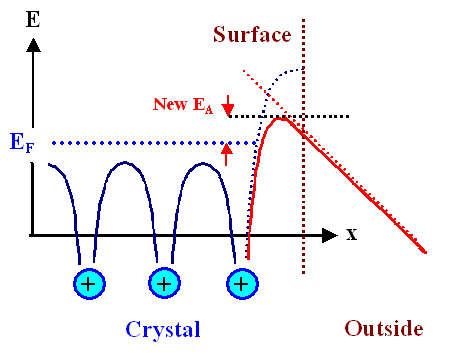
The field emission effect requires a somewhat different consideration.
- Lets look at the extremes of the Schottky effect. For really high field strengths the potential barrier gets even lower and thinner, it may look somewhat like this:

Now the tunneling effect may occur. It is a phenomenon inherent in quantum mechanics and allows electron "waves" to "tunnel" through a potential barrier.
- In other words, the value of the wave function ψ for an electron does not got to zero abruptly at a potential barrier, but decays exponentially. There is then a finite amplitude for ψ on the other side of the potential barrier, an effect that is felt if the barrier is "thin" and low - as in the picture above. If the field strength is high enough, large quantities of electrons can directly tunnel to the outside world. More about tunnelling in the link.
Field emission thus is a purely quantum mechanical effect; there is no classical counterpart whatsoever. It is used in a growing number of applications:
- Electron microscopes for special purposes (e.g. scanning electron microscopes with high resolution at low beam voltage, a must for the chip industry) are usually equipped with field emission "guns".
- "Scanning Tunnelling Microscopes" (STM) which are used to view surfaces with atomic resolution, directly employ tunnelling effects.
- Large efforts are being made to construct flat panel displays with millions of miniature field emission cathodes - at least one per pixel.
- Some semiconductor devices (e.g. the "tunnel diode") depend on tunnelling effects through space charge regions.
In other contexts, tunnelling is not useful, but may limit what you can do. Most notorious, perhaps, is the effect that very thin insulators - say 5 nm and below - are insulating no more, a growing problem for the chip industry.

