6.2: Instrumentation Amplifiers
- Page ID
- 3580
There are numerous applications where a differential signal needs to be amplified. These include low-level bridge measurements, balanced microphone lines, communications equipment, thermocouple amplifiers, and the like. The immediate answer to these applications is the differential op amp configuration noted in Chapter Four. There are limitations to this form unfortunately. For starters, it is practically impossible to achieve matched high impedance inputs while maintaining high gain and satisfactory offset and noise performance. For that matter, the input impedances are not isolated; indeed, the impedance of one input may very well be a function of the signal present on the other input. Simply put, this is an unacceptable situation when a precision amplifier is needed, particularly if the source impedance is not very low.
An instrumentation amplifier overcomes these problems. Instrumentation amplifiers offer very high impedance, isolated inputs along with high gain, and excellent CMRR performance. Some people like to think of instrumentation amplifiers as a form of “souped up” differential amplifier. Instrumentation amplifiers can be fashioned from separate op amps. They are also available on a single IC for highest performance.
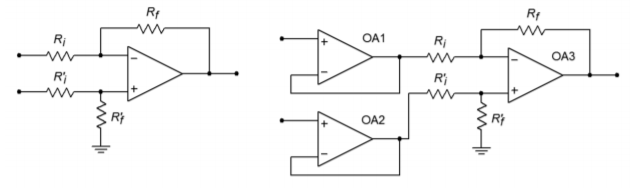
Figure \(\PageIndex{1}\): Basic differential amplifier (left) and with buffers (right).
Instrumentation amplifiers are, in essence, a three-amplifier design. To understand how they work, it is best to start with a differential amplifier based on a single op amp, as seen in Figure \(\PageIndex{1a}\). One way to increase the input impedances and also maintain input isolation, is to place a voltage follower in front of each input. This is shown in Figure \(\PageIndex{1b}\). The source now drives the very high input impedance followers. The followers exhibit very low output impedance and have no trouble driving the differential stage. In this circuit, op amp 3 is used for common-mode rejection as well as for voltage gain. Note that the gain-bandwidth requirement for op amp 3 is considerably higher than for the input followers. An enhancement to this circuit is shown in Figure \(\PageIndex{2}\). Here, op amps 1 and 2 are used for signal gain along with their previous duty of input buffering. The major problem with this configuration is that it requires very close matching of resistors in order to keep the gains the same. Any mismatch in gain between the two inputs will result in a degradation of CMRR. For optimum common-mode rejection, the undesired signal must be identical at the inputs to op amp 3. For high CMRR systems, resistor matching may need to be better than 0.01%. This is an expensive requirement if discrete resistors are used. Another way around this would be to allow some adjustment of the gain to compensate for gain mismatches, perhaps by using a resistor/potentiometer combination in place of \(R_f^{'}\) for op amp 3. For reasons of cost and time, adjustments are frowned upon.
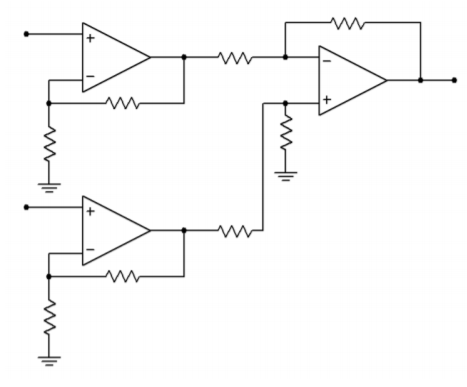
Figure \(\PageIndex{2}\): Basic instrumentation amplifier.
Fortunately, there is a very slight modification to Figure \(\PageIndex{2}\) that will remove the problem of mismatched gains. This modification involves joining the \(R_i\) values of op amps 1 and 2 into a single resistor. This is shown in Figure \(\PageIndex{3}\). In order to prevent possible confusion with op amp 3, the three resistors used for the input section have been labeled as \(R_1\), \(R_2\), and \(R_3\). In order to analyze this circuit, we will use the approximation techniques examined earlier.
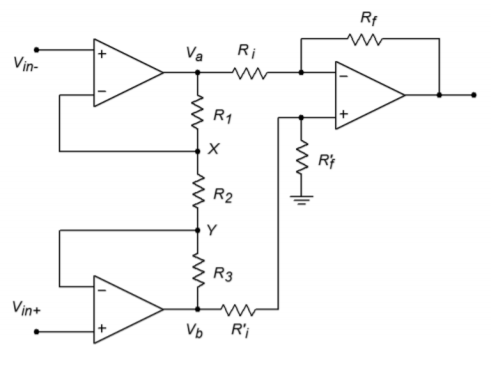
Figure \(\PageIndex{3}\): Improved instrumentation amplifier.
First of all, from preceding work we already know the gain Equation for the differential section
\[ V_{out} = \frac{R_f}{R_i} (V_b − V_a) \label{6.1} \]
Our goal, then, is to find equations for \(V_b\) and \(V_a\). Let's examine op amp 1 for \(V_a\). First, due to the approximation that the error voltage of the op amps is zero, the inverting and noninverting inputs of each op amp are the same. We can therefore say that \(V_x\) must equal \(V_{in-}\), and that \(V_y\) must equal \(V_{in+}\).
\[ V_x = V_{in-} \label{6.2} \]
\[ V_y = V_{in+} \label{6.3} \]
The output voltage \(V_a\) must equal \(V_x\) plus the drop across \(R_1\).
\[ V_a = V_x + V_{R1} \label{6.4} \]
The “positive” potential of \(V_{R1}\) is arbitrary. We are assuming that the current is flowing down through \(R_1\). If the actual numbers work out opposite, \(V_{R1}\) will come up negative. The voltage drop \(V_{R1}\) is found by Ohm's Law:
\[ V_{R1} = R_1 I_{R1} \label{6.5} \]
To expand,
\[ I_{R1} = I_{R2} + I_{opamp 1} \nonumber \]
\(I_{opamp 1}\) is approximately 0, therefore,
\[ V_{R1} = R_1 I_{R2} \nonumber \]
The current through \(R_2\) is set by its value and the drop across it.
\[ I_{R2} = \frac{V_x − V_y}{R_2} \label{6.6} \]
Substituting \ref{6.6} and \ref{6.5} into \ref{6.4} yields
\[ V_a = V_x + \frac{R_1 (V_x−V_y)}{R_2} \label{6.7} \]
Substituting \ref{6.2} and \ref{6.3} into \ref{6.7} yields
\[ V_a = V_{in-} + \frac{R_1 (V_{in-} − V_{in+})}{R_2} \nonumber \]
\[ V_a = V_{in-} + \frac{R_1}{R_2} (V_{in-} − V_{in+}) \nonumber \]
\[ V_a = V_{in-} + V_{in-} \frac{R_1}{R_2} – V_{in+} \frac{R_1}{R_2} \nonumber \]
\[ V_a = V_{in-} \left( 1 + \frac{R_1}{R_2} \right) – V_{in+} \frac{R_1}{R_2} \label{6.8} \]
A close look at Equation \ref{6.8} reveals that it is made up of two terms. The first term is \(V_{in-}\) times the noninverting gain of op amp 1, as you may have expected. The second term is \(V_{in+}\) times the inverting gain of op amp 1. This output potential is important to note. Even though it may not appear as though op amp 1 will clip a given signal, it might if the input to the second op amp is large enough and of the proper polarity.
By a similar derivation, the Equation for \(V_b\) is found
\[ V_b = V_{in+} \left( 1+ \frac{R_3}{R_2} \right) – V_{in-} \frac{R_3}{R_2} \label{6.9} \]
For gain matching, \(R_3\) is set equal to \(R_1\). \(R_2\) can then be used to control the gain of the input pair, in tandem.
Finally, substituting \ref{6.8} and \ref{6.9} into \ref{6.1} yields,
\[ V_{out} = \frac{R_f}{R_i}\left(\left( V_{in+}\left( 1+ \frac{R_1}{R_2} \right) – V_{in-} \frac{R_1}{R_2} \right) − \left( V_{in-} \left( 1+ \frac{R_1}{R_2} \right) – V_{in+} \frac{R_1}{R_2} \right)\right) \label{6.10} \]
Combining terms produces
\[ V_{out} = \frac{R_f}{R_i} \left( \left(V_{in+} − V_{in-} \right) \left( 1+ \frac{R_1}{R_2} \right) + \left( V_{in+} − V_{in-} \right) \frac{R_1}{R_2} \right) \nonumber \]
\[ V_{out} = (V_{in+} − V_{in-}) \left(\frac{R_f}{R_i}\right)\left( 1+2 \frac{R_1}{R_2} \right) \label{6.11} \]
The first term is the differential input voltage. The second term is the gain produced by op amp 3, and the third term is the gain produced by op amps 1 and 2. Note that the system common-mode rejection is no longer solely dependent on op amp 3. A fair amount of common-mode rejection is produced by the first section, as evidenced by Equations \ref{6.8} and \ref{6.9}. Because the inverting and noninverting gains are almost the same for very high values, high input gains tend to optimize the system CMRR. The remaining common-mode signals can then be dealt with by op amp 3.
Example \(\PageIndex{1}\)
The instrumentation amplifier of Figure \(\PageIndex{4}\) is used to amplify the output of a balanced microphone. The output of the microphone is 6 mV peak (12 m differential), and a common-mode hum signal is induced into the lines at 10 mV peak (0 mV differential). If the system has a CMRR of 100 dB, what is the output signal?
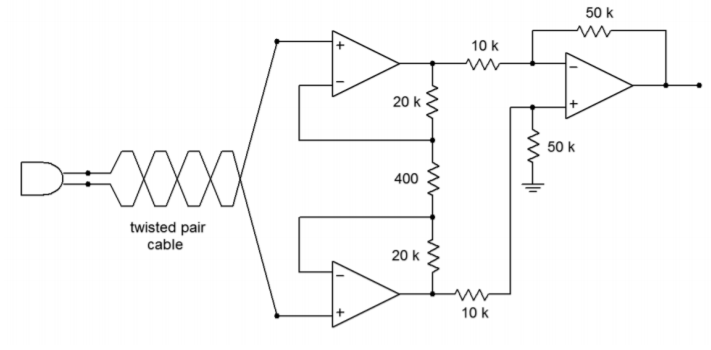
Figure \(\PageIndex{4}\): Instrumentation amplifier for Example \(\PageIndex{1}\).
First, let's check the outputs of the first section to make sure that no clipping is occurring. We will use superposition and consider the desired signal and hum signal separately.
\[ V_a = V_{in-} ( 1+ \frac{R_1}{R_2} ) – V_{in+} \frac{R_1}{R_2} \nonumber \]
\[ V_a = −6mV ( 1+ \frac{20 k}{400} ) – 6 mV \frac{20 k}{400} \nonumber \]
\[ V_a = −306mV−300mV \nonumber \]
\[ V_a = −606mV \nonumber \]
Performing the same calculation on the hum signal produces a contribution of
\[ V_a =10 mV \left( 1+ \frac{20 k}{400} \right) −10mV \frac{20 k}{400} \nonumber \]
\[ V_a = 10 mV \nonumber \]
For worst case, these two components' magnitudes add, yielding 616 mV, which is far below clipping. The same results are produced for \(V_b\), except that the desired signal is positive.
Now for the output voltage. The second section has a gain of
\[ A_v = \frac{R_f}{R_i} \nonumber \]
\[ A_v = \frac{50 k}{10 k} \nonumber \]
\[ A_v = 5 \nonumber \]
The desired differential input signal is \(V_b - V_a\), so
\[ V_{out} = A_v (V_b−V_a) \nonumber \]
\[V_{out} = 5(606mV−(−606mV)) \nonumber \]
\[ V_{out} = 6.06 V \nonumber \]
This result may also be produced in one step by using Equation \ref{6.11}
\[ V_{out} = (V_{in+} − V_{in-}) \frac{R_f}{R_i} (1+2 \frac{R_1}{R_2}) \nonumber \]
\[ V_{out} = 12mV \frac{50 k}{10 k} (1+2 \frac{20 k}{400}) \nonumber \]
\[ V_{out} = 6.06 V \nonumber \]
Note that the total gain is 505. Because this amplifier is not perfect, some common-mode signal gets through. It is suppressed by 100 dB over a desired signal. 100 dB translates to a factor of \(10^5\) in voltage gain. To find the hum signal at the output, multiply the hum by the ordinary signal gain, and then divide it by the CMRR
\[ V_{hum} = V_{out (cm)} \nonumber \]
\[ V_{out (cm)} = V_{in (cm)} \frac{A_v}{CMRR} \nonumber \]
\[ V_{out (cm)} = 10 mV \frac{505}{10^5} \nonumber \]
\[ V_{out (cm)} = 50.5 \mu V \nonumber \]
Notice how the hum signal started out just as large as the desired signal, but is now many times smaller. The very high CMRR of the instrumentation amplifier is what makes this possible.
Computer Simulation
In Figure \(\PageIndex{5}\), Multisim is used to simulate the amplifier of Example \(\PageIndex{1}\). The simple 3-terminal op amp model is used here. In order to clearly see the common-mode rejection, the desired differential input signal is set to a 1 mV sine wave, and the common-mode signal is set to 1 V DC. The initial bias solution shows that op amps 1 and 2 amplify both the AC and DC portions of the input, while common-mode rejection is left up to op amp 3. This is evidenced by the fact that the input nodes of the final op amp both see the same DC potential. At the output, the sine wave has been amplified by approximately 500 as expected. There is no DC offset at the output, indicating rejection of the common-mode DC signal.
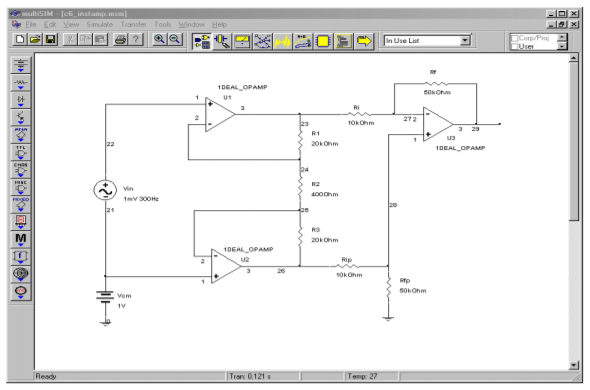
Figure \(\PageIndex{5a}\): Instrumentation amplifier in Multisim.
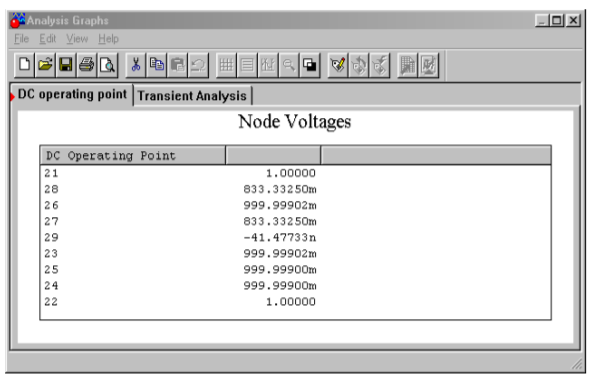
Figure \(\PageIndex{5b}\): DC voltages for instrumentation amplifier.
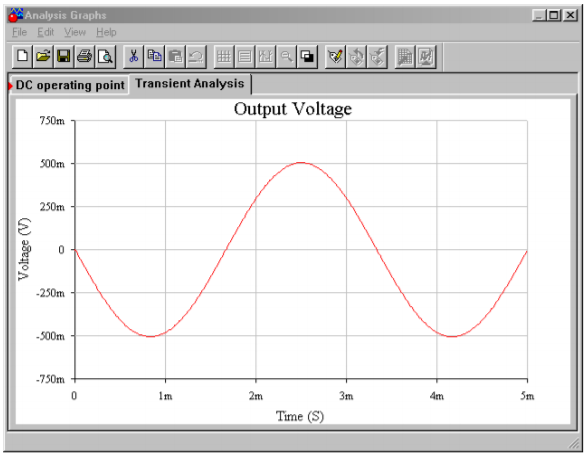
Figure \(\PageIndex{5c}\): AC output voltage for instrumentation amplifier.
Having seen how useful instrumentation amplifiers are, it should come as no surprise to find that manufacturers have produced these devices on a single IC. One such device is the LT1167 from Linear Technology. This amplifier is suited for a variety of applications including bridge amplifiers and differential to single-ended converters. It is very similar in layout to Figure \(\PageIndex{3}\), using 24.7 k\(\Omega\) resistors for \(R_1\) and \(R_3\), and 10 k\(\Omega\) resistors for \(R_i\) and \(R_f\). It features a typical CMRR of 115 dB for gains of 10, and up to 140 dB for gains of 1000. Its input resistance is 200 G\(\Omega\) minimum. The gain is set by placing an appropriate resistor between the gain set pins. The gain may be approximated as
\[ A_v = 1+ \frac{49.4 k\Omega}{R_g} \nonumber \]
For superior high frequency performance, some instrumentation amplifiers include connections for a guard drive. This is shown in Figure \(\PageIndex{6}\).
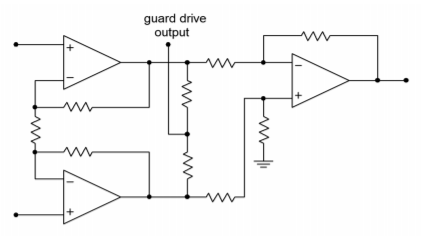
Figure \(\PageIndex{6}\): Guard drive internal connections.
This signal is derived from the outputs of the first section. By using two equalvalued resistors, the differential signals cancel, and thus the guard-drive signal is equal to the common-mode signal. This signal will then be buffered and used to drive the shields of the input wires as shown in Figure \(\PageIndex{7}\).
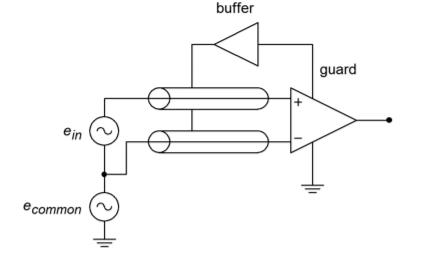
Figure \(\PageIndex{7}\): Guard drive.
To understand how performance is improved, refer to Figure \(\PageIndex{8}\). Here, the cables are replaced with a simple model. \(R\) represents the cable resistance and \(C\) represents the cable capacitance. The cable model is little more than a lag network. As you know, this causes high frequency roll off and phase change. If the two sections are not identical, the rolloffs and phase changes will not be the same in the two lines. These changes will affect the common-mode signal and can lead to a degradation of the system CMRR. In the guard-drive circuit, the cable shields are not connected to ground at the source signal. They are only connected to the guard-buffer output. This is an important point. By driving the shield with a signal equal to the common-mode signal, the voltage developed across \(C\) will be zero. Both ends of the capacitor see the same potential; therefore, the drop is nonexistent. This reduces the cable effects considerably.
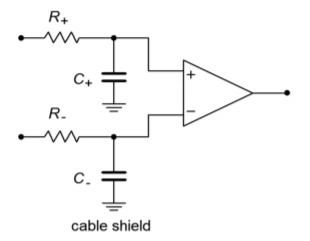
Figure \(\PageIndex{8}\): Unbalanced lag network equivalents.
Example \(\PageIndex{2}\)
The signal produced by a transducer in a factory automation system provides a nominal level of 0.1 V. For proper use, the signal needs to be amplified up to 1 V. Because this signal must pass through the relatively noisy (electrically speaking) environment of the production floor, a balanced cable with an instrumentation amplifier is appropriate. Using the LT1167, design a circuit to meet these requirements.
For the power supply, a standard \(\pm\)15 V unit will suffice. \(R_g\) is used to set the desired gain of ten.
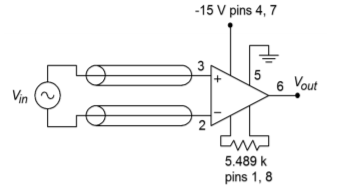
Figure \(\PageIndex{9}\): Completed instrumentation amplifier for Example \(\PageIndex{2}\).
\[ A_v = 1+ \frac{49.4 k}{R_g} \nonumber \]
\[ R_g = \frac{49.4 k}{A_v −1} \nonumber \]
\[ R_g = \frac{49.4 k}{10−1} \nonumber \]
\[ R_g = 5.489 k \nonumber \]
The completed circuit is shown in Figure \(\PageIndex{9}\).


