7.4: Function Generation
- Page ID
- 3589
Function generation circuits are used to create arbitrary transfer characteristics. These can be used for a variety of purposes, including transducer linearization and sine shaping. Indeed, many modern laboratory signal generators do not directly create a sine wave; rather, they generate a triangle wave and pass it through a function circuit, which will then produce the desired sine wave. In essence, a function circuit gives different gains to different parts of the input signal. It impresses its shape on the input waveform. If a “straight sided” waveform such as a ramp or triangle is fed into a function circuit, the resulting output waveform will bear a striking resemblance to the circuit's transfer curve. (This effect can be put to good use when investigating function circuits via computer simulation.)
Basically, there are two ways in which to create a function circuit with an op amp. The first way is an extension of the Zener limiter circuit. The second form relies on a biased-diode network. In both cases, the base circuit form is that of an inverting voltage amplifier. Also, both techniques allow the resulting transfer curve's slope to increase or decrease at specified break points and rates.
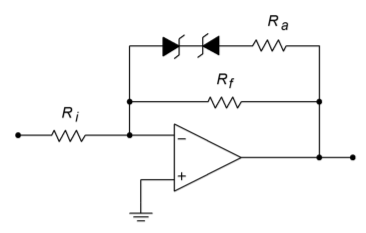
Figure \(\PageIndex{1}\): Simple function generator.
A simple function circuit is shown in Figure \(\PageIndex{1}\). Note that it is very similar to the limiter of Figure 7.27. The only difference is the inclusion of \(R_a\). Below the Zener potential, the circuit gain is still set by \(R_f\). When the Zener potential is eventually reached, the diodes can no longer force the output to an unchanging value, as \(R_a\) is in series with them. Instead of an ideal shunt across \(R_f\) as in the limiter, Rf is effectively paralleled by \(R_a\). In other words, once the Zener potential is reached, the gain drops to \((R_f || R_a)/R_i\). This is shown in Figure \(\PageIndex{2}\). To be a bit more precise, the gain change is not quite so abrupt as this approximation. In reality, the transfer curve is smoother and somewhat delayed, as indicated by the dashed line.
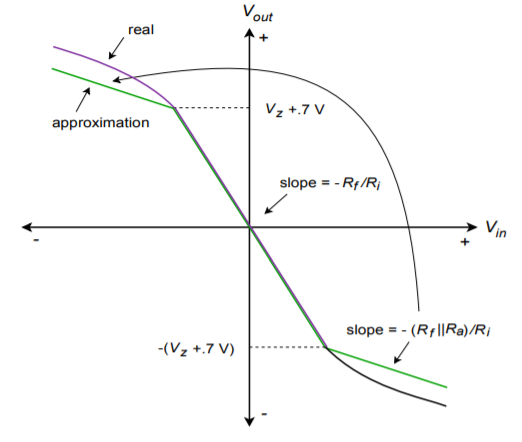
Figure \(\PageIndex{2}\): Transfer characteristic (decreasing slope).
In order to achieve an increasing slope, the Zener/resistor combination is placed in parallel with Ri. When the Zener potential is reached, \(R_a\) will effectively parallel \(R_i\), reducing gain. This has the unfortunate side effect of reducing the input impedance,so it may be necessary to include an input buffer. An example circuit and resulting transfer curve are shown in Figure \(\PageIndex{3}\).
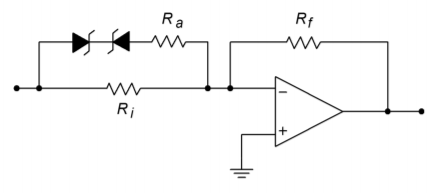
Figure \(\PageIndex{3a}\): Simple function generator, increasing gain.
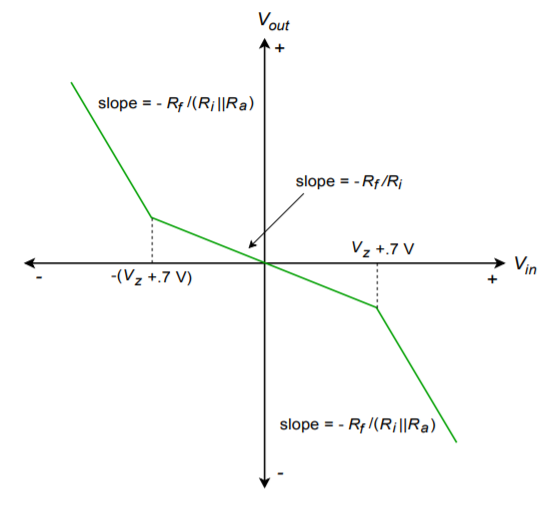
Figure \(\PageIndex{3b}\): Transfer characteristic, increasing slope.
If more than two slopes are required, it is possible to parallel multiple Zener/resistor combinations. This technique can be used to create a piece-wise linear approximation of a desired transfer characteristic. A two-section circuit is shown in Figure \(\PageIndex{4}\). Note how the resistors are constantly placed in parallel, thus reducing gain. If this multiple-section technique is used with a circuit such as the one in Figure \(\PageIndex{3}\), the gain will increase.
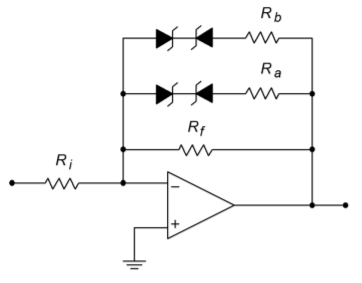
Figure \(\PageIndex{4a}\): Multiple section function generator.
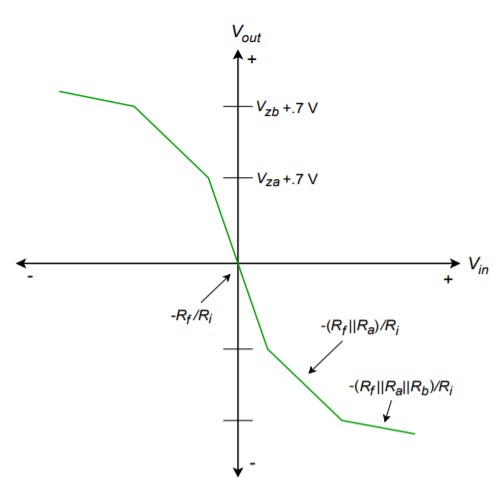
Figure \(\PageIndex{4b}\): Transfer characteristic for multiple section generator.
Example \(\PageIndex{1}\)
Given the circuit in Figure \(\PageIndex{5}\), sketch its transfer curve.
The first step is to note the break points in the curve. Because this circuit uses a decreasing gain scheme with diodes across \(R_f\), the output break points are set by the Zener potentials. Also note that the break points are symmetrical about zero as identical diodes are used.
\[ V_{break} = \pm (V_z + 0.7V) \nonumber \]
\[ V_{break} = \pm (3.9 V + 0.7 V) \nonumber \]
\[ V_{break} = \pm 4.6 V \nonumber \]
The next item to determine is the base voltage gain. This is the gain without the Zener/resistor effect.
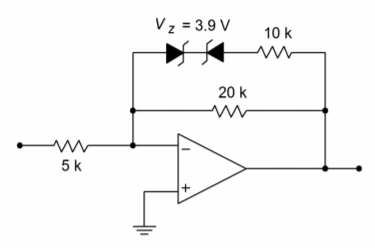
Figure \(\PageIndex{5}\): Function generator for Example \(\PageIndex{1}\).
\[ A_v = \frac{−R_f}{R_i} \nonumber \]
\[ A_v = \frac{-20 k}{5 k} \nonumber \]
\[ A_v = −4 \nonumber \]
The second level gain occurs when the diodes are on, placing \(R_a\) in parallel with \(R_f\).
\[ A_{v2} = \frac{−R_f || R_a}{R_i} \nonumber \]
\[ A_{v2} = \frac{−20 k ||10 k}{5 k} \nonumber \]
\[ A_{v2} = −1.33 \nonumber \]
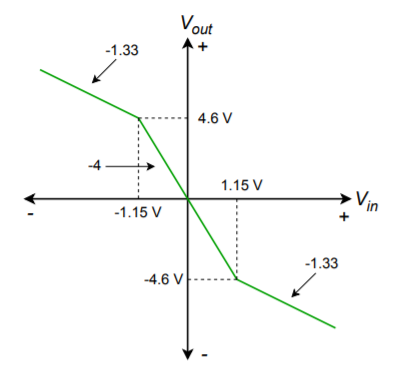
Figure \(\PageIndex{6}\): Transfer characteristic of the circuit in Figure \(\PageIndex{5}\).
The resulting plot is shown in Figure \(\PageIndex{6}\). In order to find the break point for the input signal (in this case only the output break is found), you need to divide the output break by the slope of the transfer curve. For an output of 4.6 V, the input signal will be 4 times less at 1.15 V. If multiple sections are used, the changes due to each section are added in order to find the corresponding input signal. If the circuit is an increasing-gain type (as in Figure \(\PageIndex{3}\)), then the input break points are known, and the output points are found by multiplying by the slope. Both of these items are illustrated in the following example.
Example \(\PageIndex{2}\)
Draw the transfer curve for the circuit of Figure \(\PageIndex{7}\).
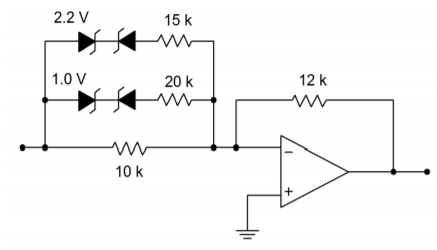
Figure \(\PageIndex{7}\): Multiple section circuit for Example \(\PageIndex{2}\).
All diode pairs are identical, so symmetry is maintained. By inspection, the input break points are:
\[ V_{break1-in} = 1.0 V + 0.7 V = 1.7 V \nonumber \]
\[ V_{break1-in} = 2.2 V+0.7 V=2.9 V \nonumber \]
The base gain is
\[ A_v = − \frac{R_f}{R_i} \nonumber \]
\[ A_v = − \frac{12 k}{10 k} \nonumber \]
\[ A_v = −1.2 \nonumber \]
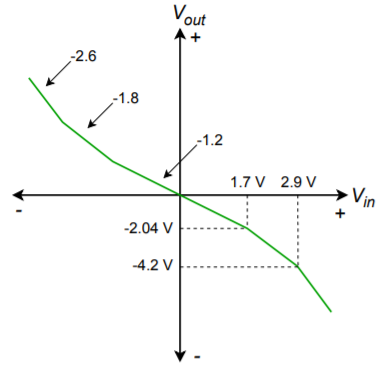
Figure \(\PageIndex{8}\): Characteristic of multiple section circuit of Figure \(\PageIndex{7}\).
The second level gain is
\[ A_{v2} =− \frac{R_f}{R_i || R_a} \nonumber \]
\[ A_{v2} =− \frac{12 k}{10 k ||20 k} \nonumber \]
\[ A_{v2} =−1.8 \nonumber \]
The third level gain is
\[ A_{v3} =− \frac{R_f}{R_i ||R_a ||R_b} \nonumber \]
\[ A_{v3} =− \frac{12 k}{10 k ||20 k ||15 k} \nonumber \]
\[ A_{v3} =−2.6 \nonumber \]
The corresponding output breaks are
\[ V_{break1-out} = A_v V_{break1-in} \nonumber \]
\[ V_{break1-out} = −1.2×1.7 \nonumber \]
\[ V_{break1-out} = −2.04 V \nonumber \]
\[ V_{break2-out} = V_{break1-out} + A_{v2} (V_{break2-in} – V_{break1-in}) \nonumber \]
\[ V_{break2-out} = −2.04 V+(−1.8)×(2.9 V−1.7 V) \nonumber \]
\[ V_{break2-out} = −4.2 V \nonumber \]
The resulting curve is shown in Figure \(\PageIndex{8}\).
Example \(\PageIndex{3}\)
A temperature transducer's response characteristic is plotted in Figure \(\PageIndex{9}\). Unfortunately, the response is not consistent across a large temperature range. At very high or low temperatures, the device becomes more sensitive.
Design a circuit that will compensate for this error, so that the output will remain at a sensitivity of 1 V/10 C\(^{\circ}\) over a large temperature range.
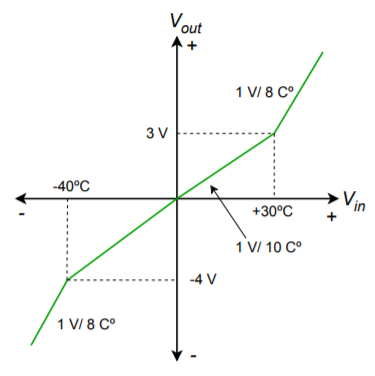
Figure \(\PageIndex{9}\): Temperature transducer's response for Example \(\PageIndex{3}\).
First of all, in order to compensate for an increasing curve, a mirror image decreasing curve is called for. The circuit will only need a single diode section; however, it will not be symmetrical. The positive break occurs at 30 degrees (3 V), and the negative break occurs at -40 degrees (-4 V). In this range the gain will remain at unity. Outside of this range, the gain must fall. In order to bring a ratio of 1 V/8 C\(^{\circ}\) back to 1 V/10 C\(^{\circ}\), it must be multiplied by its reciprocal - a gain of 8/10. The desired transfer curve is shown in Figure \(\PageIndex{10}\).

Figure \(\PageIndex{10}\): Desired transfer curve for Example \(\PageIndex{3}\).
If \(R_f\) and \(R_i\) are arbitrarily chosen to be 10 k\(\Omega\), the resulting combination of \(R_a||R_f\) must be 8 k\(\Omega\) to achieve this gain. \(R_a\) can then be found:
\[ R_a || R_f = 8 k \nonumber \]
\[ \frac{1}{R_a} + \frac{1}{10 k} = \frac{1}{8 k} \nonumber \]
\[ R_a = 40 k \nonumber \]
Because the break points have already been determined to be 3 and -4 V respectively, all that needs to be done is to compensate for the forward drop of the other diode.
\[ V_{z+} = 3 V − 0.7 V \nonumber \]
\[ V_{z+} = 2.3 V \nonumber \]
\[ V_{z-} = −(4 V − 0.7 V) \nonumber \]
\[ V_{z-} = −3.3 V \text{ (use absolute value)} \nonumber \]
Because this circuit inverts the signal, it may be wise to include an inverting buffer to compensate. The resulting circuit is shown in Figure \(\PageIndex{11}\).
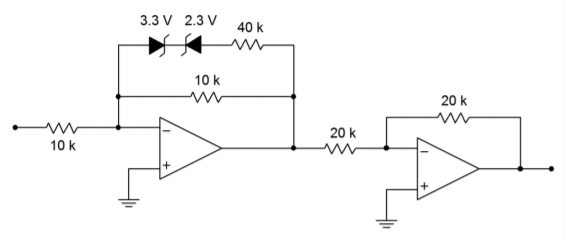
Figure \(\PageIndex{11}\): Correction circuit for the transducer in Example \(\PageIndex{3}\).
One of the problems with the Zener form is that the transfer curves change slope slowly. Because of this, fine control over the shape is not very easy to come by. Consequently, a good deal of trial and error is sometimes needed during the design sequence. Also, there is a limited range of Zener diode values available. A form that is somewhat more precise utilizes a biased-diode network.
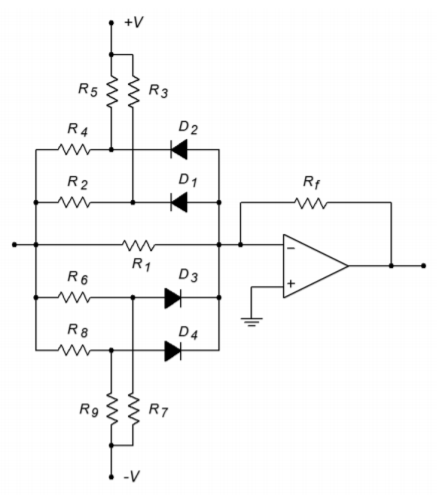
Figure \(\PageIndex{12}\): Biased diode function generator.
An increasing gain-function circuit that utilizes a biased-diode approach is shown in Figure \(\PageIndex{12}\). Its corresponding transfer curve is shown in Figure \(\PageIndex{13}\). For each break point, one diode and a pair of resistors are required. Even if the break points are symmetrical for positive and negative inputs, one set of components will be required for each polarity. The basic concept is the same as that of the Zener approach; by turning on sections with higher and higher input voltages, resistors will be placed in parallel with the base feedback resistors, thus changing the gain. As with the Zener approach, a decreasing gain characteristic is formed by placing the network across \(R_f\), instead of \(R_i\). Let's take a look at how a single section reacts.
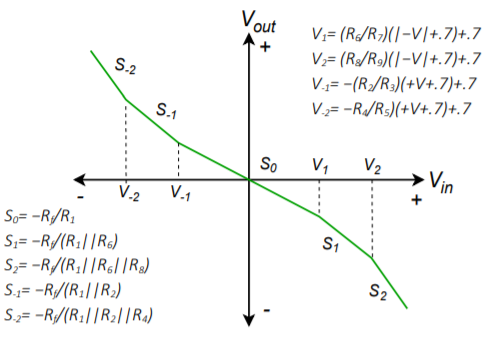
Figure \(\PageIndex{13}\): Transfer characteristic of biased diode function generator.
Each break point requires a blocking diode, a gain resistor and a bias resistor. Resistors \(R_2\) and \(R_3\), along with diode \(D_1\) make up a single section for negative input voltages. Under low signal conditions, \(D_1\) is off and blocks current flow. Effectively, the section is an open circuit. If the input potential goes negative enough, \(D_1\) will turn on, thus placing \(R_2\) in parallel with \(R_1\) and increasing the gain. The slope (gain) of the transfer curve is:
\[ \text{Slope } = − \frac{R_f}{R_1 || R_2} \nonumber \]
The break point occurs when the cathode of \(D_1\) goes to approximately -0.7 V (assuming silicon). At this point, the drop across \(R_3\) must be
\[ V_{R_3} = V_{CC} + 0.7 V \nonumber \]
The drop across \(R_2\) must be
\[ V_{R_2} = V_{in} − 0.7 V \nonumber \]
Right before \(D_1\) conducts, the current through \(R_2\) must equal the current through \(R_3\).
\[\frac{V_{R_3}}{R_3} = \frac{V_{R_2}}{R_2} \nonumber \]
\[ \frac{V_{CC} + 0.7 V}{R_3} = \frac{V_{in} − 0.7 V}{R_2} \nonumber \]
At this instant, \(V_{in}\) equals the break point. Solving for \(V_{in}\) gives,
\[ V_{in} = V_{breakpoint} = R_2 R_3 (V_{CC} + 0.7 V) + 0.7 V \nonumber \]
or to a rough approximation,
\[ V_{breakpoint} \approx \frac{R_2}{R_3} V_{CC} \nonumber \]
The approximation error may be minimized by using germanium diodes. Note that since the break points are set by a resistor ratio, very tight control of the curve is possible. When designing a function circuit, the required slopes dictate the values of the gain resistors. For ease of use the bias potentials are set to the positive and negative supply rails. Given these elements and the desired break point voltages, the necessary bias resistor values may be calculated.
Computer Simulation
A simulation using the biased diode technique is presented in Figure \(\PageIndex{14}\). Here the circuit has been designed to echo the response found in Figure \(\PageIndex{16}\) from Example \(\PageIndex{1}\).
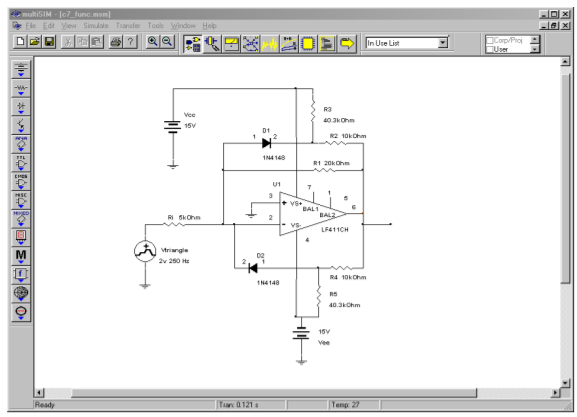
Figure \(\PageIndex{14a}\): Biased diode function synthesizer in Multisim.
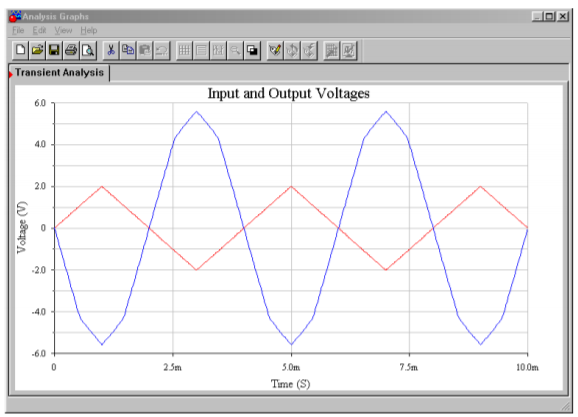
Figure \(\PageIndex{14b}\): Function synthesizer waveforms.
Note that the same values are used here for the feedback resistors as those found in the Zener version of the circuit. The only new calculation was for the biasing resistors (the 40.3 k\(\Omega\)) to set the output breakpoints. In order to see the gain effect clearly, a triangle wave is used as the input. Because the input waveform consists of nice, straight, diagonal lines, the gain response will be reflected in the output wave-shape. This is obvious in the Transient Analysis graph. The signal inversion stands out, but the more interesting and important item is the change in slope that occurs when the output waveform reaches about 4.5 volts. This is approximately where the output breakpoint was calculated to be, and the reduction in gain above this point is quite apparent.


