9.3: Quantifier Rules
- Page ID
- 53869
\(\def\Atom#1#2{ { \mathord{#1}(#2) } }\)
\(\def\Bin{ {\mathbb{B}} }\)
\(\def\cardeq#1#2{ { #1 \approx #2 } }\)
\(\def\cardle#1#2{ { #1 \preceq #2 } }\)
\(\def\cardless#1#2{ { #1 \prec #2 } }\)
\(\def\cardneq#1#2{ { #1 \not\approx #2 } }\)
\(\def\comp#1#2{ { #2 \circ #1 } }\)
\(\def\concat{ { \;\frown\; } }\)
\(\def\Cut{ { \text{Cut} } }\)
\(\def\Discharge#1#2{ { [#1]^#2 } }\)
\(\def\DischargeRule#1#2{ { \RightLabel{#1}\LeftLabel{\scriptsize{#2} } } }\)
\(\def\dom#1{ {\operatorname{dom}(#1)} }\)
\(\def\Domain#1{ {\left| \Struct{#1} \right|} }\)
\(\def\Elim#1{ { {#1}\mathrm{Elim} } }\)
\(\newcommand{\Entails}{\vDash}\)
\(\newcommand{\EntailsN}{\nvDash}\)
\(\def\eq[#1][#2]{ { #1 = #2 } }\)
\(\def\eqN[#1][#2]{ { #1 \neq #2 } }\)
\(\def\equivclass#1#2{ { #1/_{#2} } }\)
\(\def\equivrep#1#2{ { [#1]_{#2} } }\)
\(\def\Exchange{ { \text{X} } }\)
\(\def\False{ { \mathbb{F} } }\)
\(\def\FalseCl{ { \lfalse_C } }\)
\(\def\FalseInt{ { \lfalse_I } }\)
\(\def\fCenter{ { \,\Sequent\, } }\)
\(\def\fdefined{ { \;\downarrow } }\)
\(\def\fn#1{ { \operatorname{#1} } }\)
\(\def\Frm[#1]{ {\operatorname{Frm}(\Lang #1)} }\)
\(\def\fundefined{ { \;\uparrow } }\)
\(\def\funimage#1#2{ { #1[#2] } }\)
\(\def\funrestrictionto#1#2{ { #1 \restriction_{#2} } }\)
\(\newcommand{\ident}{\equiv}\)
\(\newcommand{\indcase}[2]{#1 \ident #2\text{:}}\)
\(\newcommand{\indcaseA}[2]{#1 \text{ is atomic:}}\)
\(\def\indfrm{ { A } }\)
\(\def\indfrmp{ { A } }\)
\(\def\joinrel{\mathrel{\mkern-3mu}}\)
\(\def\lambd[#1][#2]{\lambda #1 . #2}\)
\(\def\Lang#1{ { \mathcal{#1} } }\)
\(\def\LeftR#1{ { {#1}\mathrm{L} } }\)
\(\def\len#1{ {\operatorname{len}(#1)} }\)
\(\def\lexists#1#2{ { \exists #1\, #2 } }\)
\(\def\lfalse{ {\bot} }\)
\(\def\lforall#1#2{ { \forall#1\, #2 } }\)
\(\newcommand{\lif}{\rightarrow}\)
\(\newcommand{\liff}{\leftrightarrow}\)
\(\def\Log#1{ { \mathbf{#1} } }\)
\(\def\ltrue{ {\top} }\)
\(\def\Id#1{ {\operatorname{Id}_#1} }\)
\(\def\Int{ {\mathbb{Z}} }\)
\(\def\Intro#1{ { {#1}\mathrm{Intro} } }\)
\(\def\mModel#1{ { \mathfrak{#1} } }\)
\(\newcommand{\mSat}[3][{}]{\mModel{#2}{#1}\Vdash{#3}}\)
\(\newcommand{\mSatN}[3][{}]{\mModel{#2}{#1}\nVdash{#3}}\)
\(\def\Nat{ {\mathbb{N}} }\)
\(\def\nicefrac#1#2{ {{}^#1/_#2} }\)
\(\def\num#1{ { \overline{#1} } }\)
\(\newcommand{\Obj}[1]{\mathsf{#1}}\)
\(\def\Rat{ {\mathbb{Q}} }\)
\(\def\Real{ {\mathbb{R}} }\)
\(\def\RightR#1{ { {#1}\mathrm{R} } }\)
\(\def\Part#1#2{ { \Atom{\Obj P}{#1, #2} } }\)
\(\def\pto{ { \hspace{0.1 cm}\to\hspace{-0.44 cm}\vcenter{\tiny{\hbox{|}}}\hspace{0.35 cm} } }\)
\(\def\PosInt{ {\mathbb{Z}^+} }\)
\(\def\Pow#1{ {\wp(#1)} }\)
\(\newcommand{\Proves}{\vdash}\)
\(\newcommand{\ProvesN}{\nvdash}\)
\(\def\Relbar{\mathrel{=}}\)
\(\newcommand{\Sat}[3][{}]{\Struct{#2}{#1}\vDash{#3}}\)
\(\newcommand{\SatN}[3][{}]{\Struct{#2}{#1}\nvDash{#3}}\)
\(\newcommand{\Sequent}{\Rightarrow}\)
\(\def\Setabs#1#2{ { \{#1:#2\} } }\)
\(\newcommand{\sFmla}[2]{#1\,#2}\)
\(\def\Struct#1{ {#1} }\)
\(\def\subst#1#2{ { #1/#2 } }\)
\(\def\Subst#1#2#3{ { #1[\subst{#2}{#3}] } }\)
\(\def\TMblank{ { 0 } }\)
\(\newcommand{\TMendtape}{\triangleright}\)
\(\def\TMleft{ { L } }\)
\(\def\TMright{ { R } }\)
\(\def\TMstay{ { N } }\)
\(\def\TMstroke{ { 1 } }\)
\(\def\TMtrans#1#2#3{ { #1,#2,#3 } }\)
\(\def\Trm[#1]{ {\operatorname{Trm}(\Lang #1)} }\)
\(\def\True{ { \mathbb{T} } }\)
\(\newcommand{\TRule}[2]{#2#1}\)
\(\def\tuple#1{ {\langle #1 \rangle} }\)
\(\newcommand{\Value}[3][\,]{\mathrm{Val}_{#1}^{#3}(#2)}\)
\(\def\Var{ { \mathrm{Var} } }\)
\(\newcommand{\varAssign}[3]{#1 \sim_{#3} #2}\)
\(\def\Weakening{ { \text{W} } }\)
Rules for \(\lforall{}{}\)

In the rules for \(\lforall{}{}\), \(t\) is a ground term (a term that does not contain any variables), and \(a\) is a constant symbol which does not occur in the conclusion \(\lforall{x}{A(x)}\), or in any assumption which is undischarged in the derivation ending with the premise \(A(a)\). We call \(a\) the eigenvariable of the \(\Intro{\lforall{}{}}\) inference.
Rules for \(\lexists{}{}\)
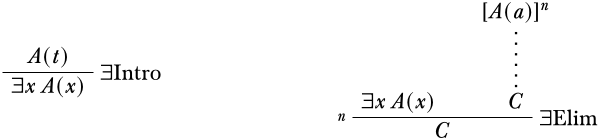
Again, \(t\) is a ground term, and \(a\) is a constant which does not occur in the premise \(\lexists{x}{A(x)}\), in the conclusion \(C\), or any assumption which is undischarged in the derivations ending with the two premises (other than the assumptions \(A(a)\)). We call \(a\) the eigenvariable of the \(\Elim{\lexists{}{}}\) inference.
The condition that an eigenvariable neither occur in the premises nor in any assumption that is undischarged in the derivations leading to the premises for the \(\Intro{\lforall{}{}}\) or \(\Elim{\lexists{}{}}\) inference is called the eigenvariable condition.
We use the term “eigenvariable” even though \(a\) in the above rules is a constant. This has historical reasons.
In \(\Intro{\lexists{}{}}\) and \(\Elim{\lforall{}{}}\) there are no restrictions, and the term \(t\) can be anything, so we do not have to worry about any conditions. On the other hand, in the \(\Elim{\lexists{}{}}\) and \(\Intro{\lforall{}{}}\) rules, the eigenvariable condition requires that the constant symbol \(a\) does not occur anywhere in the conclusion or in an undischarged assumption. The condition is necessary to ensure that the system is sound, i.e., only derives sentences from undischarged assumptions from which they follow. Without this condition, the following would be allowed:
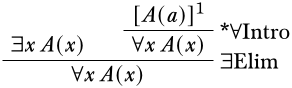
However, \(\lexists{x}{A(x)} \EntailsN \lforall{x}{A(x)}\).


