9.1: Introduction
- Page ID
- 458
If we multiply the vdW EOS (expression 7.11a) by 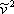 and expand the factorized product by applying the distributive law, the result is the vdW EOS expressed in terms of molar volume, as follows:
and expand the factorized product by applying the distributive law, the result is the vdW EOS expressed in terms of molar volume, as follows:
\[\bar{v}^{3}-\left(b+\frac{R T}{P}\right) \bar{v}^{2}+\left(\frac{a}{P}\right) \bar{v}-\frac{a b}{P}=0 \label{9.1}\]
Note that Equation \ref{9.1} is a third order polynomial in \(\bar{v}\) i.e., it is cubic in molar volume. Additionally, we can substitute the definition of compressibility factor \(Z\),
\[Z=\frac{P \bar{v}}{R T} \label{9.2}\]
into Equation \ref{9.1} and obtain a different cubic polynomial in \(Z\), as shown:
\[Z^{3}-\left(1+\frac{b P}{R T}\right) Z^{2}+\left(\frac{a P}{R^{2} T^{2}}\right) Z-\frac{a b P^{2}}{(R T)^{3}}=0 \label{9.3}\]
As we see, vdW EOS is referred to as cubic because it is a polynomial of order 3 in molar volume (and hence in compressibility factor \(Z\)). In general, any equation of state that is cubic in volume (and \(Z\)) and explicit in pressure (Equation 7.11b) is regarded as a cubic equation of state. vdW EOS is a cubic EOS, and all the transformations and modifications that it has undergone during the more than one hundred years since its publication are also cubic EOS; or better, they are in-the-van-der-Waals-spirit EOS or of-the-van-der-Waals-family EOS.
Contributors and Attributions
Prof. Michael Adewumi (The Pennsylvania State University). Some or all of the content of this module was taken from Penn State's College of Earth and Mineral Sciences' OER Initiative.


