13.2: SPC- Basic Control Charts- Theory and Construction, Sample Size, X-Bar, R charts, S charts
- Page ID
- 22523
Authors: Chris Bauman, Jennifer De Heck, Evan Leonard, Merrick Miranda
Stewards: Eric Black, Stacy Young, Dan Carter, Megan Boekeloo
Introduction
Control charts are one of the most commonly used methods of Statisical Process Control (SPC), which monitors the stability of a process. The main features of a control chart include the data points, a centerline (mean value), and upper and lower limits (bounds to indicate where a process output is considered "out of control").They visually display the fluctuations of a particular process variable, such as temperature, in a way that lets the engineer easily determine whether these variations fall within the specified process limits. Control charts are also known as Shewhart charts after Walter Shewhart, who developed them in the early 1900’s.
Control Chart Background
A process may either be classified as in control or out of control. The boundaries for these classifications are set by calculating the mean, standard deviation, and range of a set of process data collected when the process is under stable operation. Then, subsequent data can be compared to this already calculated mean, standard deviation and range to determine whether the new data fall within acceptable bounds. For good and safe control, subsequent data collected should fall within three standard deviations of the mean. Control charts build on this basic idea of statistical analysis by plotting the mean or range of subsequent data against time. For example, if an engineer knows the mean (grand average) value, standard deviation, and range of a process, this information can be displayed as a bell curve, or population density function (PDF). The image below shows the control chart for a data set with the PDF overlay.
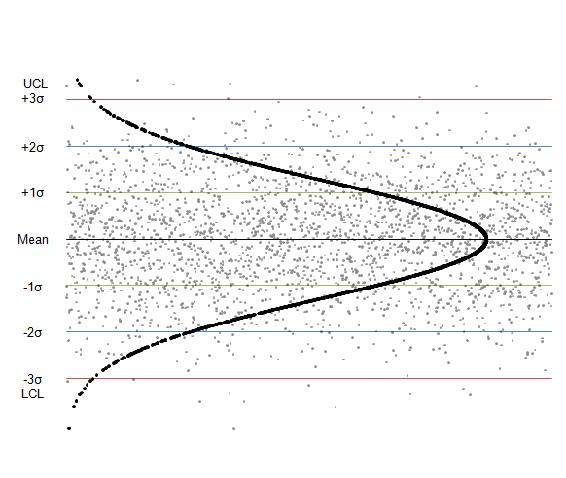
The centerline is the mean value of the data set and the green, blue and red lines represent one, two, and three standard deviations from the mean value. In generalized terms, if data points fall within three standard deviations of the mean (within the red lines), the process is considered to be in control. These rules are discussed in greater detail later in this section.
Control Charts are commonly used in six sigma control today, as a means of overall process improvement. For more on six-sigma control, see six sigma.
Control Chart Functions
The main purpose of using a control chart is to monitor, control, and improve process performance over time by studying variation and its source. There are several functions of a control chart:
- It centers attention on detecting and monitoring process variation over time.
- It provides a tool for ongoing control of a process.
- It differentiates special from common causes of variation in order to be a guide for local or management action.
- It helps improve a process to perform consistently and predictably to achieve higher quality, lower cost, and higher effective capacity.
- It serves as a common language for discussing process performance.
Sample Size and Subgrouping
There are a few key conditions that must be met when constructing control charts:
- The initial predictions for the process must be made while the process is assumed to be stable. Because future process quality will be compared to these predictions, they must be based off of a data set that is taken while the operation is running properly.
- Multiple subsets of data must be collected, where a subset is simply a set of n measurements taken over a specific time range. The number of subsets is represented as k. A subset average, subset standard deviation, and subset range will be computed for each subset.
- From these subsets, a grand average, an average standard deviation, and an average range are calculated. The grand average is the average of all subset averages. The average standard deviation is simply the average of subset standard deviations. The average range is simply the average of subset ranges.
The upper and lower control limits for the process can then be determined from this data.
- Future data taken to determine process stability can be of any size. This is because any point taken should fall within the statistical predictions. It is assumed that the first occurrence of a point not falling within the predicted limits shows that the system must be unstable since it has changed from the predictive model.
- The subsets are defined, based on the data and the process. For example, if you were using a pH sensor, the sensor would most likely output pages of data daily. If you know that your sensor has the tendency to drift every day, you might select a 30 minute subset of data. If it drifts monthly you might set your subset to be 24 hours or 12 hours.
- Finally, the population size, N is assumed to be infinite. Alternatively, if the population is finite but the sample size is less than 5% of the population size, we can still approximate the population to be near infinite. That is, n/N <= 0.05 where n is the sample size and N is the population size. [5]
X-Bar, R-Charts, and S-Charts
There are three types of control charts used determine if data is out of control, x-bar charts, r-charts and s-charts. An x-bar chart is often paired with either an r-chart or an s-chart to give a complete picture of the same set of data.
Pairing X-Bar with R-Charts
X-Bar (average) charts and R (range) -charts are often paired together. The X-Bar chart displays the centerline, which is calculated using the grand average, and the upper and lower control limits, which are calculated using the average range. Future experimental subsets are plotted compared to these values. This demonstrates the centering of the subset values. The R-chart plots the average range and the limits of the range. Again, the future experimental subsets are plotted relative to these values. The R-chart displays the dispersion of the subsets. X-Bar/R-Chart plot a subgroup average. Note that they should only be used when subgroups really make sense. For example, in a Gage R&R study, when operators are testing in duplicates or more, subgrouping really represents the same group.
Pairing X-Bar with S-Charts
Alternatively, X-Bar charts can be paired with S-charts (standard deviation). This is typically done when the size of the subsets are large. For larger subsets, the range is a poor statistic to estimate the distributions of the subsets, and instead, standard deviation is used. In this case, the X-Bar chart will display control limits that are calculated using the average standard deviation. The S-Charts are similar to the R-charts; however, instead of the range, they track the standard deviation of multiple subsets.
Smoothing Data with a Moving Average
If it is desired to have smooth data, the moving average method is one option. This method involves taking the average of a number of points, and using that average for the middle data point. From this point on, the data is treated the same as any normal group of k subsets. Though this method will produce a smoother curve, it has a lag in detecting points, which may be problematic if the points are out of the acceptable range. This time lag would keep the control system from reacting to the problem until after the average is found. For this reason, moving average charts are appropriate mainly for slower processes that can handle the lag.
For example, let us calculate a value for a set of data which takes samples every second. We will use an average of 10 points to find this, however, in practice there is no set number of data points that should be used. For the point t = 50, we must wait until data has been collected through t = 54. The points are then averaged for t = 45-54 and used as the function value. For the next point, t = 51, the average of the points for t = 46-55 are used, and so on. If this is still confusing, please see moving average for a more detailed explanation.
Reading Control Charts
Control charts can determine whether a process is behaving in an "unusual" way.
Note: The upper and lower control limits are calculated using the grand average and either the average range and average sigma. Example calculations are shown in the Creating Control Charts Section.
The quality of the individual points of a subset is determined unstable if any of the following occurs:
- Rule 1: Any point falls beyond 3σ from the centerline(this is represented by the upper and lower control limts).
- Rule 2: Two out of three consecutive points fall beyond 2σ on the same side of the centerline.
- Rule 3: Four out of five consecutive points fall beyond 1σ on the same side of the centerline.
- Rule 4: Nine or more consecutive points fall on the same side of the centerline.
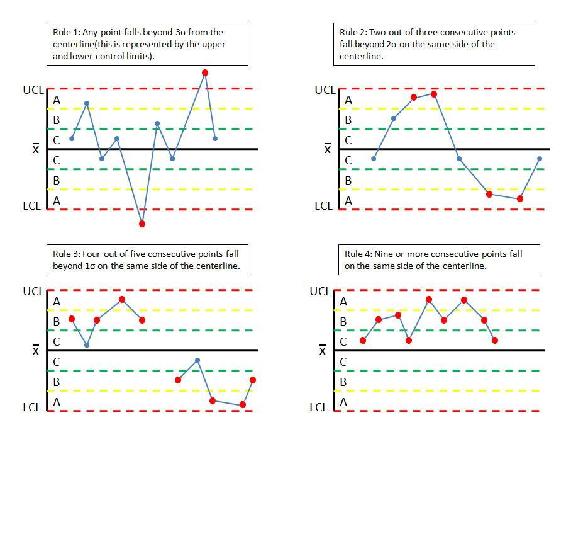
The quality of a subset is determined unstable according to the following rules:
1. Any subset value is more than three standard deviations from the centerline.
2. Two consecutive subset values are more than two standard deviations from the centerline and are on the same side of the centerline.
3. Three consecutive subset values are more than one standard deviation from the centerline and are on the same side of the centerline.
Creating Control Charts
To establish upper and lower control limits on control charts, there are a number of methods. We will discuss the method for the number of components in a subset, n, less than 15. For methods involving n > 15 and other techniques, see Process Control and Optimization, Liptak, 2.34. Here, the table of constants for computing limits, and the limit equations are presented below.
Please note that Table A below does NOT contain data for a sample problem. Any time you make a control chart, you refer to this table. The values in the table are used in the equations for the upper control limit (UCL), lower control limit (LCL), etc. This will be explained in the examples below. If you are interested in how these constants were derived, there is a more detailed explanation in Control Chart Constants.
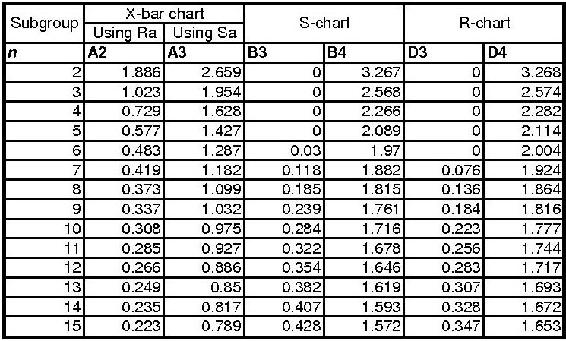
Table A: Table of Constants
To determine the value for n, the number of subgroups
In order to determine the upper (UCL) and lower (LCL) limits for the x-bar charts, you need to know how many subgroups (n) there are in your data. Once you know the value of n, you can obtain the correct constants (A2, A3, etc.) to complete your control chart. This can be confusing when you first attend to create a x-bar control chart. The value of n is the number of subgroups within each data point. For example, if you are taking temperature measurements every min and there are three temperature readings per minute, then the value of n would be 3. And if this same experiment was taking four temperature readings per minute, then the value of n would be 4. Here are some examples with different tables of data to help you further in determining n:
Example 1: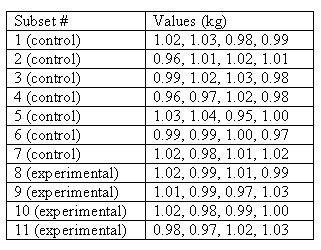
n= 4 since there are four readings of kg.
Example 2: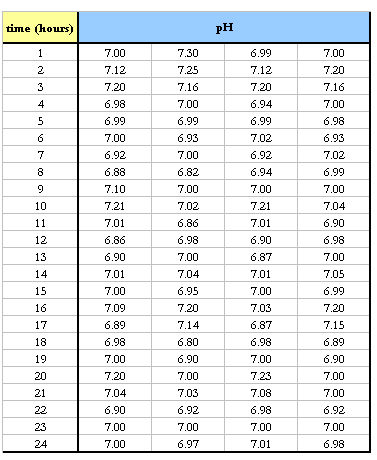
n= 4 since there are four readings of pH.
Example 3: 
n= 3 since there are three readings of temperature.
After creating multiple control charts, determining the value of n will become quite easy.
Calculating UCL and LCL
For the X-Bar chart the following equations can be used to establish limits, where 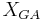 is the grand average,
is the grand average, 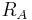 is the average range, and
is the average range, and  is the average standard deviation.
is the average standard deviation.
Calculating Grand Average, Average Range and Average Standard Deviation
To calculate the grand average, first find the average of the n readings at each time point. The grand average is the average of the averages at each time point.
To calculate the grand range, first determine the range of the n readings at each time point. The grand range is the average of the ranges at each time point.
To calculate the average standard deviation, first determine the standard deviation of the n readings at each time point. The average standard deviation is the average of the standard deviations at each time point.
Note: You will need to calculate either the grand range or the average standard deviation, not both.
For X-bar charts, the UCL and LCL may be determined as follows:
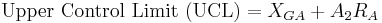
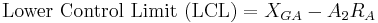
Alternatively,  can be used as well to calculate UCL and LCL:
can be used as well to calculate UCL and LCL:
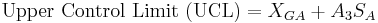
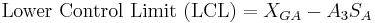
The centerline is simply 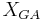 .
.
For R-charts, the UCL and LCL may be determined as follows:
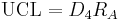
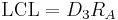
The centerline is the value 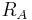 .
.
For S-charts, the UCL and LCL may be determined as follows:
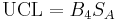
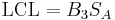
The centerline is  .
.
The following flow chart demonstrates the general method for constructing an X-bar chart, R-chart, or S-chart:

Calculating Region Boundaries
To determine if your system is out of control, you will need to section your data into regions A, B, and C, below and above the grand average. These regions are shown in Figure III. To calculate the boundaries between these regions, you must first calculate the UCL and LCL. The boundaries are evenly spaced between the UCL and LCL. One way to calculate the boundaries is shown below.
Boundary between A and B above XGA = XGA + (UCL − XGA) * 2 / 3
Boundary Between B and C above XGA = XGA + (UCL − XGA) * 1 / 3
Boundary Between A and B below XGA = LCL + (XGA − LCL) * 2 / 3
Boundary Between B and C below XGA = LCL + (XGA − LCL) * 2 / 3
Example 1
Assume that in the manufacture of 1 kg Mischmetal ingots, the product weight varies with the batch. Below are a number of subsets taken at normal operating conditions (subsets 1-7), with the weight values given in kg. Construct the X-Bar, R-charts, and S-charts for the experimental data (subsets 8-11). Measurements are taken sequentially in increasing subset number.

Solution:
First, the average, range, and standard deviation are calculated for each subset.
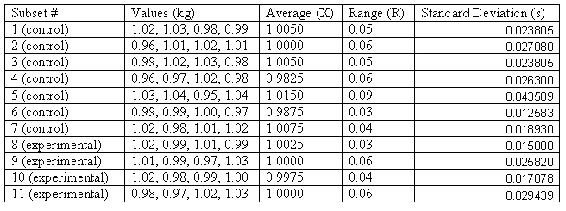
Next, the grand average XGA, average range RA, and average standard deviation SA are computed for the subsets taken under normal operating conditions, and thus the centerlines are known. Here n=4.
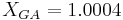
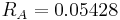
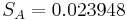
X-Bar limits are computed (using 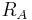 ).
).
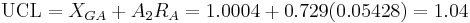
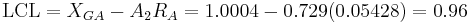
X-Bar limits are computed (using  ).
).
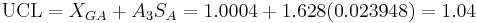

Note: Since n=4 (a relatively small subset size), both  and
and  can be used to accurately calculate the UCL and LCL.
can be used to accurately calculate the UCL and LCL.
R-chart limits are computed.
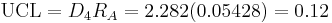
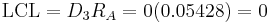
S-chart limits are computed.

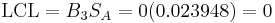
The individual points in subsets 8-11 are plotted below to demonstrate how they vary with in comparison with the control limits.
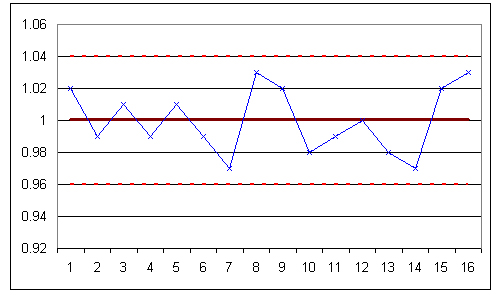
The subgroup averages are shown in the following X-Bar chart:
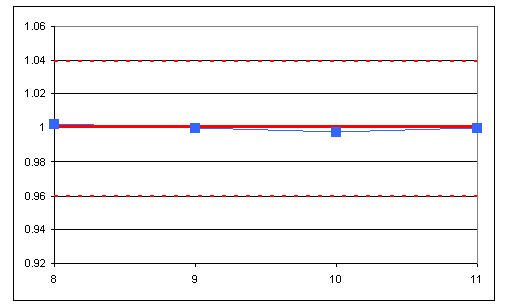
The R-chart is shown below:
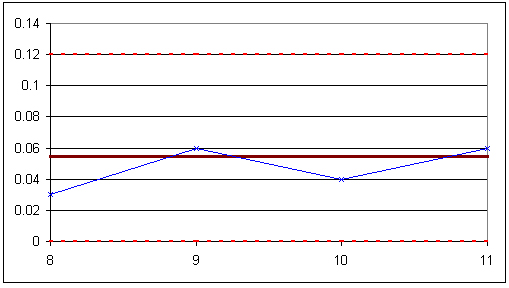
The S-chart is shown below:
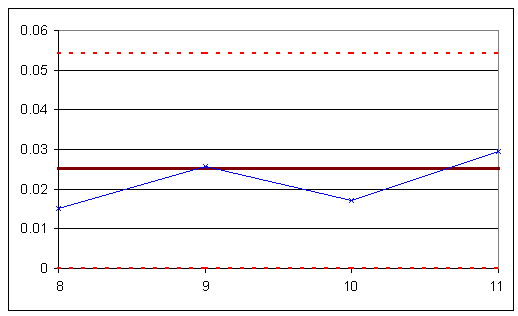
The experimental data is shown to be in control, as it obeys all of the rules given above.
Example 2
It’s your first day on the job as a chemical engineer in a plant, and one of your responsibilities is to monitor the pH of a particular process. You are asked by your boss to monitor the stability of the system. She gives you some baseline data for the process, and you collect data for the process during your first day. Construct X-bar and R-Charts to report your results.
Table 1: Baseline data

To be consistent with the baseline data, each hour you take four pH readings. The data you collect is displayed below.
Table 2: Experimental data

Solution
For this situation, there are k=24 subsets because there are 24 data sets. For each subset, n=4 because there are four pH measurements taken each hour. The first thing you do is calculate the mean and range of each subset. The means are calculated using the AVERAGE() Excel function and the ranges are calculated using MAX() – MIN(). Once these values are calculated, the Grand Average XGA and average range RA are calculated. These values are simply the means of each subset’s mean and range. This data is displayed below.
Table 3: Data used to calculate and grand average and Range.
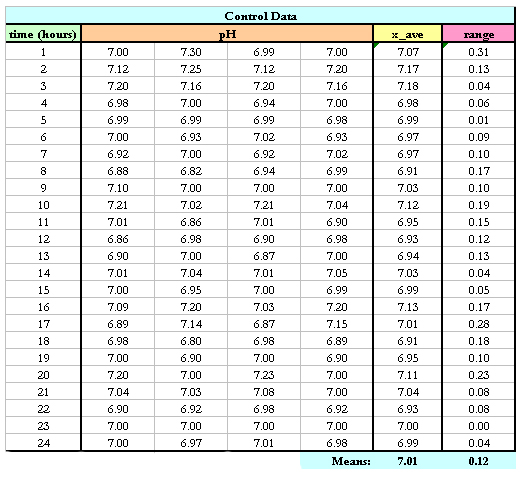
Now that you know XGA = 7.01 and RA = 0.12, you can calculate the upper control limit, UCL, and lower control limit, LCL, for the X-bar control chart.
From Table A, A2 = 0.729 when n=4. Using equations UCL and LCL for X-bar charts listed above:
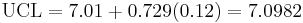
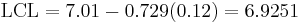
Then the UCL = 7.0982, LCL = 6.9251 and XGA = 7.01 are plotted in Excel along with the average values of each subset from the experimental data to produce the X-bar control chart.
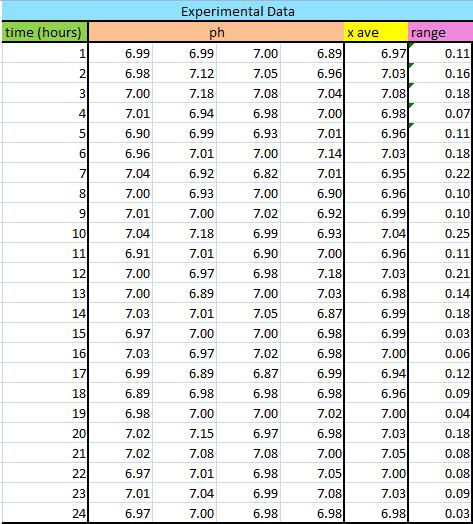
Table 4: Average subset values and ranges plotted on the X-bar and R-chart
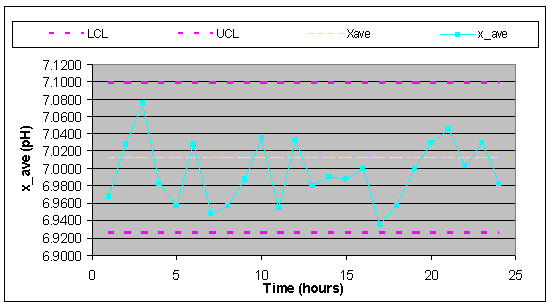
Then, to construct the Range charts, the upper and lower control limits were found. For n=4, D3 = 0 and D4 = 2.282 so then:
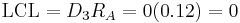
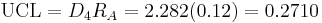
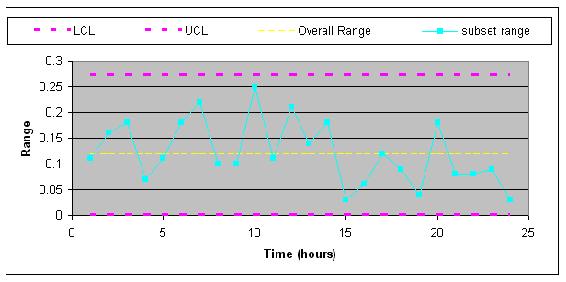
From both of these charts, the process is in control because all rules for stabilty are met.
Rule 1: No point falls beyond the UCl and LCL.
Rule 2: Two out of three consecutive points do not fall beyond 2σ on the same side of the centerline.
Rule 3: Four out of five consecutive points do not fall beyond 1σ on the same side of the centerline.
Rule 4: Nine or more consecutive points do not fall on the same side of the centerline.
It's important that both of these charts be used for a given set of data because it is possible that a point could be beyond the control band in the Range chart while nothing is out of control on the X-bar chart.
Another issue worth noting is that if the control charts for this pH data did show some points beyond the LCL or UCL, this does not necessarily mean that the process itself is out of control. It probably just means that the pH sensor needs to be recalibrated.
Example 3
A simple out-of-control example with a sample constructed control chart.
You have been analyzing the odd operation of a temperature sensor in one of the plant's CSTR reactors. This particular CSTR's temperature sensor consists of three small thermocouples spaced around the reactor: T1, T2, and T3. The CSTR is jacketed and cooled with industrial water. The reaction taking place in the reactor is moderately exothermic. You know the thermocouples are working fine; you just tested them, but a technician suggests the CSTR has been operating out of control for the last 10 days. There have been daily samples taken and there is a control chart created from the CSTR's grand average and standard deviation from the year's operation.
You are assigned to see if the CSTR is operating out of control. The grand average is 307.47 units of temperature and the grand standard deviation is 4.67 units of temperature. The data is provided for construction of the control chart in Table 1 and the data from the last 10 troublesome days is shown in Table 2. You decide to plot the troublesome data onto the control chart to see if it violates any stability rules.
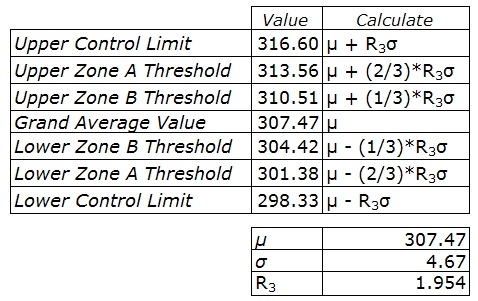
Table 3-1. Data for Construction of Control Chart
The way I found A_3 or in this case, R_3, I used the control charts constants table which is found on this wiki page. I decided to use the x-bar using the standard deviations) but you can also use use the range). I found that the value for n(number of subgroups) is three since the CSTR's temperature sensor consists of three small thermocouples (T1,T2,T3). Therefore by looking at the constant chart, I get A_3( or R_3 in this case) to be 1.954. Here's the table below:

Also, you will notice if you used the range instead of the standard deviation to determine the UCL,LCL, etc. that the values will be roughly the same. Here's the table in comparing the values of UCL and LCL using either A_2 (range) or A_3(stdev):
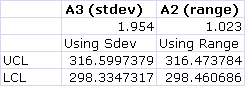
Note: These values were using the same grand average (307.47), the grand standard deviation (4.67) and the grand range (8.80)
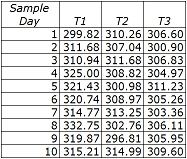
Table 3-2. Sample Data from Past 10 Troublesome Days
Solution
When the sample data was graphed onto the control chart, the image below was seen.
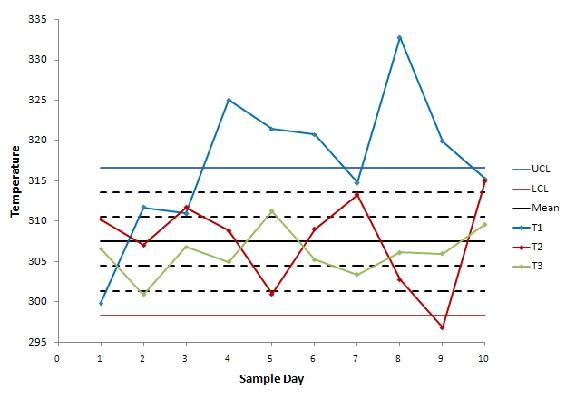
We can see from the control chart that the CSTR system is clearly out of control. Each thermocouple was tested to see which stability rules it violates.
The first thermocouple (T1) violates every stability rule.
- Rule 1 - Several points from the T1 data fall above the upper control line.
- Rule 2 - There are many instances where at least two out of three consecutive points fall above the zone AB threshold.
- Rule 3 - There are eight consecutive points falling above the BC threshold.
- Rule 4 - Nine consecutive points fall above the mean value.
Judging on this thermocouple's performance, we can say that the system is out of control, but we will analyze the other thermocouples' performance for good measure.
The second thermocouple (T2) violates stability rule 1, 2, and 3.
- Rule 1 - One point falls below the lower control line.
- Rule 2 - Two consecutive points (samples 9 and 10) fall beyond the AB threshold.
- Rule 3 - Of the last five samples from T2, four are beyond the BC threshold.
The third thermocouple (T3) does not violate any stability rules and the results it displays are within control.
This system is out of control because the data from the thermocouples falls beyond the threshold rules for the unit's control chart. This could be explained with many potential situations. One is explained below.
If the CSTR's agitator is knocked loose, the agitation could become erratic. The erratic agitation could create eddy currents and hot spots in the CSTR.
The entire system is out of control because you know that the thermocouples are operating fine and more than one thermocouple violates the stability rules.
Multiple Choice Question 1
When is it useful to use a moving average data set?
A. Never
B. When instant response to process is desired
C. When you have a process that changes slowly
D. Always, as it is a far superior method
Multiple Choice Question 2
What does n signify?
A. The number of subsets in collected data
B. The number of data points in a subset
C. The upper control limit for an X-bar chart
D. The centerline for an R-chart
Multiple Choice Question 3
Of the four stability rules for reading control charts, how many must occur in order for a subset to be determined unstable?
A. 1
B. 2
C. 3
D. 4
Multiple Choice Answers
Question 1: C
Question 2: B
Question 3: A
Sage's Corner
|
SPC Control Presentation video.google.com/googleplayer...03583755378767 |
| Slides without narration SPC control |
References
- Wheeler, Donald J., and David S. Chambers. Understanding Statistical Process Control. 2nd ed. Knoxville: SPC P. 37-88. [1]
- Box, George E., William G. Hunter, and J S. Hunter. Statistics for Experimenters: An Introduction to Design, Data Analysis, and Model Building. New York: John Wiley & Sons. 43-45. [2]
- Liptak, Bela G. "Process Control and Optimization." Instrument Engineers' Handbook 4: 405-413. [3]
- Woolf, Peter, Amy Keating, Christopher Burge, and Michael Yaffe. Statistics and Probability Primer for Computational Biologists. Massachusetts Institute of Technology. 2004. [4]
- Anderson, David R., Sweeney, Dennis J. and Williams, Thomas A. Statistics for Business and Economics, 10e. Thompson South-Western. 2008. [5]


