4.3.2.3 Magnified Pressure Measurement
- Page ID
- 665
For situations where the pressure difference is very small, engineers invented more sensitive measuring device. This device is build around the fact that the height is a function of the densities difference. In the previous technique, the density of one side was neglected (the gas side) compared to other side (liquid). This technique utilizes the opposite range. The densities of the two sides are very close to each other, thus the height become large. Figure 4.7 shows a typical and simple schematic of such an instrument. If the pressure differences between \(P_1\) and \(P_2\) is small this instrument can "magnified'' height, \(h_1\) and provide "better'' accuracy reading. This device is based on the following mathematical explanation. In steady state, the pressure balance (only differences) is
\[
P_1 + g\, \rho_1 (h_1 + h_2) =
P_2 + g\, h_2\, \rho_2
\label{static:eq:pBalance}
\]
\[
P_1 - P_2 =
g \left[ \rho_2\,h_2 - \rho_1 (h_1 + h_2) \right]
\label{static:eq:pDiffB}
\]
If the light liquid volume in the two containers is known, it provides the relationship between \(h_1\) and \(h_2\). For example, if the volumes in two containers are equal then
\[
- h_1\, A_1 = h_2 \,A_2 \longrightarrow
h_1 = - \dfrac{h_2\,A_2}{A_1}
\label{static:eq:twoContainers}
\]
Liquid volumes do not necessarily have to be equal. Additional parameter, the volume ratio, will be introduced when the volumes ratio isn't equal. The calculations as results of this additional parameter does not cause a significant complications. Here, this ratio equals to one and it simplify the equation (42). But this ratio can be inserted easily into the derivations. With the equation for height (42) equation (40) becomes
\[
P_1 - P_2 =
g \,h_2 \left( \rho_2 - \rho_1 \left(1 - \dfrac{A_2}{A_1}
\right)
\right)
\label{static:eq:balanceContA}
\]
or the height is
\[
h_2 =
\dfrac{P_1 - P_2}
{g \left[ (\rho_2 - \rho_1) + \rho_1 \dfrac{A_2}{A_1}
\right] }
\label{static:eq:balanceCont}
\]
For the small value of the area ratio, \(A_2/A_1 \ll 1\), then equation (44) becomes
\[
h_2 = \dfrac{P_1 - P_2}
{g \left( \rho_2 - \rho_1 \right) }
\label{static:eq:balanceContShort}
\]
Some refer to the density difference shown in equation (45) as "magnification factor'' since it replace the regular density,
Inclined Manometer
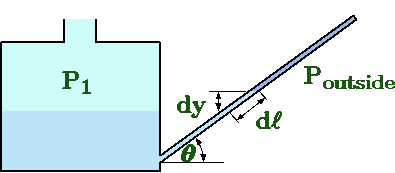
Fig. 4.8 Inclined manometer.
One of the old methods of pressure measurement is the inclined manometer. In this method, the tube leg is inclined relatively to gravity (depicted in Figure 4.8). This method is an attempt to increase the accuracy by "extending'' length visible of the tube. The equation (39) is then
\[
\label{static:eq:inclindManometer}
P_1 - P_{outside} = \rho\,g\,d\ell
\]
Inverted U-tube manometer
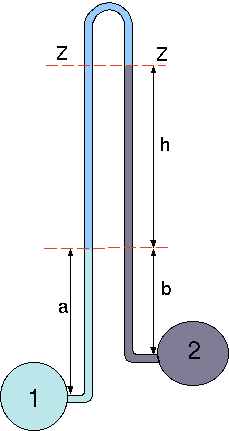
Fig. 4.9 Schematic of inverted manometer.
The difference in the pressure of two different liquids is measured by this manometer. This idea is similar to "magnified'' manometer but in reversed. The pressure line are the same for both legs on line \(ZZ\). Thus, it can be written as the pressure on left is equal to pressure on the right legs (see Figure 4.9).
\[
\label{static:eq:govInvMano}
\overbrace{P_2 - \rho_2\,(b+h) }^{\text{right leg}}\,g =
\overbrace{P_1 - \rho_1\,a - \rho\,h) }^{\text{left leg}}\,g
\]
\[
\label{static:eq:reGovInvMano}
P_2- P_1 = \rho_2\,(b+h)\,g - \rho_1\,a \,g - \rho\,h \,g
\]
For the similar density of \(\rho_1=\rho_2\) and for \(a=b\) equation (48) becomes
\[
\label{static:eq:finalInvMano}
P_2- P_1 = (\rho_1 - \rho )\,g \,h
\]
As in the previous "magnified'' manometer if the density difference is very small the height become very sensitive to the change of pressure.
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


