6.3: Conservation Moment Of Momentum
- Page ID
- 720
The angular momentum can be derived in the same manner as the momentum equation for control volume. The force
\[
\label{mom:eq:force}
F = \dfrac{D}{Dt} \int_{V_{sys}} \rho \pmb{U} dV
\]
\[
\label{mom:eq:momEqSys}
\mathfrak{M} = \pmb{r}\times \pmb{F} = \dfrac{D}{Dt} \int_{V_{sys}} \rho \, \pmb{r} \times \pmb{U}\, dV
\]
Now the left hand side has to be transformed into the control volume as
\[
\label{mom:eq:monEqCV}
\mathfrak{M} = \dfrac{d}{dt} \int_{V_{c.v.}} \rho\, \left(\pmb{r} \times \pmb{U}\right)\, dV +
\int_{S_{c.v}} \rho\,\left( \pmb{r}\times \pmb{U} \right)\pmb{U}_{rn}\, dA
\]
The angular momentum equation, applying equation (68) to uniform and steady state flow with neglected pressure gradient is reduced to
\[
\label{mom:eq:mom1D}
\mathfrak{M} = \dot{m} \left( r_2\times U_2 + r_2\times U_1 \right)
\]
Introduction to Turbo Machinery
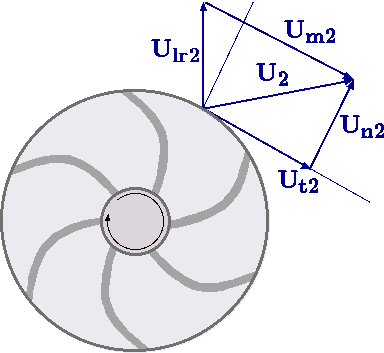
Fig. 6.9 The impeller of the centrifugal pump and the velocities diagram at the exit.
The analysis of many turbomachinary such as centrifugal pump is fundamentally based on the angular momentum. To demonstrate this idea, the following discussion is provided. A pump impeller is shown in Figure 6.9 commonly used in industry. The impeller increases the velocity of the fluid by increasing the radius of the particles. The inside particle is obtained larger velocity and due to centrifugal forces is moving to outer radius for which additionally increase of velocity occur. The pressure on the outer side is uniform thus does not create a moment. The flow is assumed to enter the impeller radially with average velocity \(U_1\). Here it is assumed that fluid is incompressible (\(\rho=constant\)). The height of the impeller is h. The exit liquid velocity, \(U_2\) has two components, one the tangential velocity, \(U_{t2}\) and radial component, \(U_{n2}\). The relative exit velocity is \(U_{lr2}\) and the velocity of the impeller edge is \(U_{m2}\). Notice that tangential liquid velocity, \(U_{t2}\) is not equal to the impeller outer edge velocity \(U_{m2}\). It is assumed that required torque is function \(U_2\), \(r\), and \(h\).
\[
\label{mom:eq:angularM}
\mathfrak{M} = \dot{m} \,r_2 \, U_{t2}
\]
\[
\label{mom:eq:angularMw}
\mathfrak{M} \,\omega = \dot{m} \,\overbrace{r_2\,\omega}^{U_{m2}} \, U_{t2}
\]
The shaft work is given by the left side and hence,
\[
\label{mom:eq:angularWork}
\dot{W} = \dot{m} \,U_{m2}\, U_{t2}
\]
The difference between \(U_{m2}\) to \(U_{t2}\) is related to the efficiency of the pump which will be discussed in the chapter on the turbomachinary.
A centrifugal pump is pumping 600 \(2[m^3/hour]\). The thickness of the impeller, \(h\) is \(2[cm]\) and the exit diameter is \(0.40[m]\). The angular velocity is 1200 \(r.p.m.\) Assume that angle velocity is leaving the impeller is \(125^{\circ}\). Estimate what is the minimum energy required by the pump.
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


