10.3.1.1: Adding Circulation to a Cylinder
- Page ID
- 783
The cylinder discussed in the previous sections was made from a dipole in a uniform flow field. It was demonstrated that in the potential flow has no resistance, and no lift due to symmetry of the pressure distribution. Thus, it was suggested that by adding an additional component that it would change the symmetry but not change the shape and hence it would provide the representation cylinder with lift. It turned out that this idea yields a better understanding of the one primary reason of lift. This results was verified by the experimental evidence. The linear characteristic (superposition principle) provides by adding the stream function of the free vortex to the previous the stream function for the case. The stream function in this case (see equation (93)) is
\[
\label{if:eq:doubletVortex}
\psi = U_0\, r \,\sin \theta \left( 1 - \left(\dfrac {r}{a}\right)^2 \right)
+ \dfrac{\Gamma }{2\,\pi} \ln \dfrac{a}{r}
\]
It can be noticed that this stream function (116) on the body is equal to \(\psi(r=a)=0\). Hence, the shape of the body remains a circle. The corresponding radial velocity in cylindrical coordinates (unchanged) and is
\[
\label{if:eq:doubletVortex:UrIni}
U_r = \dfrac{1}{r} \dfrac{\partial \psi}{\partial \theta} =
U_0\, \cos \theta \, \left( 1 - \left(\dfrac {a}{r}\right)^2 \right)
\]
\[
\label{if:eq:doubletVortex:Ur}
U_{\theta} = - \dfrac{\partial \psi}{\partial r} =
U_0\, \sin \theta \, \left( 1 + \left(\dfrac {a}{r}\right)^2 \right) +
\dfrac{\Gamma }{2\,\pi\,r}
\]
As it was stated before, examination of the stream function \(\psi=0\) is constructed. As it was constructed and discussed earlier it was observed that the location of stagnation stream function is on \(r=a\). On this line, equation (116) can be written as
\[
\label{if:eq:doubletVortex0}
0 = U_0\, r \,\sin \theta \left( 1 - \left(\dfrac {a}{r}\right)^2 \right)
+ \dfrac{\Gamma }{2\,\pi} \ln \dfrac{a}{r}
\]
or
\[
\label{if:eq:doubletVortex0a}
\sin \theta = - \dfrac{\dfrac{\Gamma }{2\,\pi} \ln \dfrac{r}{a} }
{ U_0\, r\, \left( 1 - \left(\dfrac {a}{r}\right)^2 \right) } =
\dfrac{\Gamma }{ 4\,\pi \,U_0\,\dfrac{r}{a}\, a}
\dfrac{2 \ln \dfrac{a}{r} }
{ \left( 1 - \left(\dfrac {a}{r}\right)^2 \right) } = \\
\dfrac{\Gamma }{ 4\,\pi \,U_0\,\dfrac{r}{a}\, a}
\dfrac{ \ln \left( \dfrac{a}{r} \right)^2 }
{ 1 - \left(\dfrac {a}{r}\right)^2 } =
\dfrac{\Gamma }{ 4\,\pi \,U_0\,\overline{r}\, a}
\dfrac{ \ln \left( \dfrac{1}{\overline{r}} \right)^2 }
{ 1 - \left(\dfrac {1}{\overline{r}}\right)^2 } \qquad
\]
At the point \(r=a\) the ratio in the box is approaching \(0/0\) and to examine what happen to it L'Hopital's rule can be applied. The examination can be simplified by denoting \(\xi= (a/r)^2 = \overline{r}\) and noticing that \(\xi=1\) at that point and hence
\[
\label{if:eq:doubletVortex0b}
\lim_{\xi\rightarrow 1} \dfrac{ \ln \, \xi }{ 1 - \xi } =
\lim_{\xi\rightarrow 1} \dfrac{ \dfrac{1}{\xi} }{ - 1} = - 1
\]
Hence, the relationship expressed in equation (119) as
\[
\label{if:eq:doubletVortex00}
\sin \theta = \dfrac{-\Gamma}{4\,\pi\, U_0\, a}
\]
This condition (122) limits the value of maximum circulation on the body due to the maximum value of sin function. The doublet strength maximum strength can be The condition
\[
\label{if:eq:doubletVortex:limit}
\left| \Gamma \right| \le 4\,\pi\, U_0\, a
\]
The value of doublet strength determines the stagnation points (which were moved by the free vortex so to speak). For example, the stagnation points for the value \(\Gamma= -2\,\sqrt{2- \sqrt{3}} \,\pi\,U_0\,a\) can be evaluated as
\[
\label{if:eq:doubletVortex:exmpleValue15}
\sin \theta = \dfrac{\overbrace{ box{$
{2\,\sqrt{2- \sqrt{3}} \,\pi\,U_0\,a}$ } }^{-\Gamma} }{4\,\pi\, U_0\, a} = \dfrac{\sqrt{2- \sqrt{3}}}{2}
\]
The solution for equation (theta, \(\theta\)) (124) is \(15^{\circ}\) or \(\pi/12\) and \(165^{\circ}\) or \(11\,\pi/12\). For various stagnation points can be found in similar way. The rest of the points of the stagnation stream lines are found from the equation (120). For the previous example with specific value of the ratio, \(\overline{\Gamma}\) as
\[
\label{if:eq:doubletVortex0a0}
\sin\theta =
\dfrac{ \sqrt{2- \sqrt{3}}\, a}{2\,r}\dfrac{ \ln \left( \dfrac{a}{r} \right)^2 }
{ 1 - \left(\dfrac {a}{r}\right)^2 }
\]
There is a special point where the two points are merging \(0\) and \(\pi\). For all other points stream function can be calculated from equation (116) can be written as
\[
\label{if:eq:doubletVortexPsi}
\dfrac{\psi}{U_0\,a} = \dfrac{r}{a} \,\sin \theta \left( 1 - \left(\dfrac {a}{r}\right)^2 \right)
+ \dfrac{\Gamma }{2\,\pi\,U_0\,a} \ln \dfrac{r}{a}
\]
or in a previous dimensionless form plus multiply by \(\overline{r}\) as
\[
\label{if:eq:doubletVortexPsiInterd}
\dfrac{\overline{r}\,\overline{\psi}}{\sin \theta} = \overline{r}^2 \,
\left( 1 - \left(\dfrac {1}{\overline{r}}\right)^2 \right)
+ \,\dfrac{\Gamma \overline{r}}{2\,\pi\,U_0\,a\,\sin \theta}
\ln {\overline{r}}
\]
After some rearrangement of moving the left hand side to right and denoting \(\overline{\Gamma}=\dfrac{\Gamma}{4\,\pi\,U_0\,a}\) along with the previous definition of \(\overline{\psi}=2\,n\) equation (127) becomes
\[
\label{if:eq:doubletVortexPsiGov}
0 = \overline{r}^2 - \dfrac{\overline{r}\,\overline{\psi}}{\sin \theta} - 1
+ \dfrac{2\,\overline{\Gamma}\, \overline{r} \,\ln\overline{r} }{\sin \theta}
\]
Note the sign in front the last term with the \(\Gamma\) is changed because
the ratio in the logarithm is reversed. The stagnation line occur when \(n=0\) hence equation (128) satisfied for all \(\overline{r}=1\) regardless to value of the \(\theta\). However, these are not the only solutions. To obtain the solution equation (stagnation line) (128) is rearranged as
\[
\label{if:eq:doubletVortexPsiGovR}
\theta = \sin^{-1} \left( \dfrac {2\,\overline{\Gamma}\, \overline{r} \,\ln\overline{r} }
{1 - \overline{r}^2} \right)
\]
Equation (128) has three roots (sometime only one) in the most zone and parameters. One roots is in the vicinity of zero. The second roots is around the one (1). The third and the largest root which has the physical meaning is obtained when the dominate term \(\overline{r}^2\) "takes'' control.
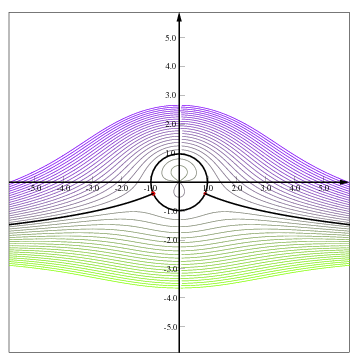
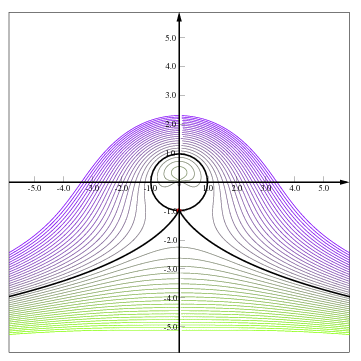
Figure 10.2 Doublet in a uniform flow with Vortex in various conditions. Typical condition for the dimensionless Vortex below on and dimensionless vortex equal to one. The figures were generated by the GLE and the program will be available on the on–line version of the book.
The results are shown in Figure 10.16. Figure ?? depicts the stream lines when the dimensionless vortex is below one. Figure 10.16(b) depicts the limiting case where the dimensionless vortex is exactly one. Once the dimensionless vortex exceeds one, the stagnation points do touch the solid body.
Example 10.8
This question is more as a project for students of Fluid Mechanics or Aerodynamics. The stream lines can be calculated in two ways. The first way is for the given \(n\), the radius can be calculated from equation (128). The second is by calculating the angle for given \(r\) from equation (129). Examine the code (attached with the source code) that was used in generating Figures 10.16 and describe or write the algorithm what was used. What is the "dead'' radius zones?
Example 10.9
Expand the GLE provided code to cover the case where the dimensionless vortex is over one (1).
Pressure Distribution Around the solid Body
The interesting part of the above analysis is to find or express the pressure around the body. With this expression the resistance and the lift can be calculated. The body reacts to static pressure, as opposed to dynamic pressure, and hence this part of the pressure needed to be evaluated. For this process the Bernoulli's equation is utilized and can be written as
\[
\label{if:eq:BernoulliEq}
P_{\theta} = P_0 - \dfrac{1}{2} \rho \left( {U_r}^2 + {U_{\theta}}^2 \right)
\]
It can be noticed that the two cylindrical components were accounted for. The radial component is zero (no flow cross the stream line) and hence the total velocity is the tangential velocity (see equation (118) where \(r=a\)) which can be written as
\[
\label{if:eq:tangentialVortex}
U_{\theta} = 2\,U_0\,\sin\theta + \dfrac{\Gamma}{2\,\pi\,a}
\]
\[
\label{if:eq:vortex:P}
P = P_0 - \dfrac{1}{2} \, \rho \left( 4\,{U_0}^2\, {\sin^2\theta} +
\dfrac{2\,U_0\,\Gamma\,\sin\theta}{\pi\,a} +
\dfrac{\Gamma^2}{4\,\pi^2\,a^2}
\right)
\]
Equation (132) is a parabolic equation with respect to \(\theta\) (\(\sin\theta\)). The symmetry dictates that D'Alembert's paradox is valid i.e that there is no resistance to the flow. However, in this case there is no symmetry around \(x\) coordinate (see Figure 10.16). The distortion of the symmetry around \(x\) coordinate contribute to lift and expected. The lift can be calculated from the integral around the solid body (stream line) and taking only the \(y\) component. The force elements is
\[
\label{if:eq:dF}
dF = -\mathbf{j} \,\mathbf{\cdot}\,P\, \mathbf{n} dA
\]
where in this case \(\mathbf{j}\) is the vertical unit vector in the downward direction, and the infinitesimal area has direction which here is broken into in the value \(dA\) and the standard direction \(\mathbf{n}\). To carry the integration the unit vector \(\mathbf{n}\) is written as
\[
\label{if:eq:unitVector}
\mathbf{n} = \mathbf{i}\,\cos\theta + \mathbf{j}\,\sin\theta
\]
The reason for definition or split (134) to take into account only the the vertical component. Using the above derivation leads to
\[
\label{if:eq:vortex:dotV}
\mathbf{j}\mathbf{\cdot}\mathbf{n} = \sin\theta
\]
The lift per unit length will be
\[
\label{if:eq:vortex:liftIntegralIni}
L = - \int_0^{2\,\pi} \left[P_0 - \dfrac{1}{2} \, \rho \left( 4\,{U_0}^2\, {\sin^2\theta} +
\dfrac{2\,U_0\,\Gamma\,\sin\theta}{\pi\,a} +
\dfrac{\Gamma^2}{4\,\pi^2\,a^2} \right) \right] \overbrace{\sin\theta}^
{\scriptscriptstyle eq. \eqref{if:eq:vortex:dotV}}
\,a\,d\theta
\]
Integration of the \(\sin\theta\) in power of odd number between \(0\) and \(2\,\pi\)is zero. Hence the only term that left from the integration (136) is
\[
\label{if:eq:vortex:integral}
L = - \dfrac{\rho\,U_0\,\Gamma}{\pi\,a}\,\int_0^{2\,\pi} \sin^2\theta d\theta
= U_0\,\rho\,\Gamma
\]
The lift created by the circulating referred as the Magnus effect which name after a Jewish scientist who live in Germany who discover or observed this phenomenon. In fact, physicists and engineers dismiss this phenomenon is ``optical illusion.'' However, the physical explanation is based on the viscosity and the vortex is the mechanism that was found to transfer the viscosity to inviscid flow.
Fig. 10.17 Schematic to explain Magnus's effect.
In certain ranges the simultaneously translate and rotation movement causes the lift of the moving object. This can be observed in a thrown ball with spin over 1000 rpm and speed in over 5 m/sec. In these parameters, the ball is moving in curved line to the target. To understand the reason for this curving, the schematic if the ball is drawn (Figure 10.17). The ball is moving to the right and rotating counter clockwise. The velocity at the top of the ball is reduced due to the rotation while the velocity at the bottom of the ball is increased. According to Bernoulli's equation, reduction or increase of the velocity changes the static pressure. Hence, the static pressure is not symmetrical and it causes a force perpendicular to the ball movement. It can be noticed the direction of the rotation changes the direction of the forces. In addition to the change of the pressure, the resistance changes because it is a function of the velocity. In many ranges the increase of the velocity increase the resistance. Hence, there are two different velocities at the top and bottom. The resistance, as a function of the velocity, is different on the bottom as compared to the top. These two different mechanisms cause the ball to move in perpendicular direction to the flow direction. The circulation mimics the Magnus's effect and hence it is used in representative flow. In the above discussion it was used for body of perfect circular shape. However, it was observed that bodies with a very complicated shape such as airplane wing, the lift can be represented by of vortex. from the numerical method of Runge–Kutta and by the Russian Zhukovsky suggest that the dimensionless nature of vortex is controlling the any shape. The extension can be done by defining the circulation as
\[
\label{if:eq:generalGamma}
\Gamma= \oint_{C} \mathbf{U} \boldsymbol{\cdot} \mathbf{ds}=\oint_{C} U\,\cos\theta\, ds
\]
Fig. 10.18 Wing in a typical uniform flow.
\[
\label{if:eq:kuttaJoukowski}
L= -\rho_\infty\, U_\infty\,\Gamma,
\]
The circulation of a ball or cylinder is easy to imagine. Yet a typical air plane do not rotate. Perhaps, the representation of inviscid flow of with vortex can represent the viscous flow. For example flow airplane wing will have typical stream line such as shown in Figure 10.18. However, the viscous flow does not behaves in this fashion especially at the trailing part of the wing. The flow around the wing sheds vortexes because the sharp turn of the flow. The sheds vortexes existence is like the free vortexes since integral including these vortexes can be included in the calculations of the circulation (see equation 10.197).
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.
2πψQ0=tan−1y
x/


