1.7.1.1: Capillarity
- Page ID
- 634
The capillary forces referred to the fact that surface tension causes liquid to rise or penetrate into area (volume), otherwise it will not be there. It can be shown that the height that the liquid raised in a tube due to the surface tension is \[h = \frac{2\sigma\cos(\beta)}{g\Delta\rho r}\] Where \(\Delta\rho\) is the difference of liquid density to the gas density and \(r\) is the radius of the tube.
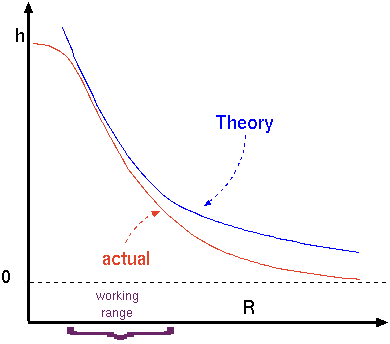
Fig. 1.24. The raising height as a function of the radii.
But this simplistic equation is unusable and useless unless the contact angle (assuming that the contact angel is constant or a repressive average can be found or provided or can be measured) is given. However, in reality there is no readily information for contact angle and therefore this equation is useful to show the treads. The maximum that the contact angle can be obtained in equation (73) when \(\beta\) = - and thus \(\cos(\beta) = 1\). This angle is obtained when a perfect half a sphere shape exist of the liquid surface. In that case equation (73) becomes \[h_{max} = \frac{2\sigma}{g\Delta\rho r}\]

Fig. 1.25. The raising height as a function of the radius.
Figure 1.25 exhibits the height as a function of the radius of the tube. The height based on equation (74) is shown in Figure 1.24 as a blue line. The actual height is shown in the red line. Equation (74) provides reasonable results only in a certain range. for a small tube radius, equation (62) proved better results because the curve approaches hemispherical sphere(small gravity effect). For large radii equation (62) approaches the strait line (the liquid line) strong gravity effect. On the other hand, for extremely small radii equation (74) indicates that the high height which indicates a negative pressure. The liquid at a certain pressure will be vaporized and will breakdown the model upon this equation was constructed. Furthermore, the small scale indicates that the simplistic and continuous approach is not appropriate and a different model is needed. The conclusion of this discussion are shown in Figure 1.24. The actual dimension for many liquids (even water) is about 1-5 \([mm]\).
The discussion above was referred to "wetting'' contact angle. The depression of the liquid occurs in a "negative'' contact angle similarly to ``wetting.'' The depression height, \(h\) is similar to equation (74) with a minus sign. However, the gravity is working against the surface tension and reducing the range and quality of the predictions of equation (74) The measurements of the height of distilled water and mercury are presented in Figure 1.25. The experimental results of these materials are with agreement with the discussion above. The surface tension of a selected material is given in Table 1.7.
In conclusion, the surface tension issue is important only in case where the radius is very small and gravity is negligible. The surface tension depends on the two materials or mediums that it separates.
Example 1.19
Calculate the diameter of a water droplet to attain pressure difference of 1000[\(N/m^2\)]. You can assume that temperature is \(20^{\circ}C\).
Solution 1.19
The pressure inside the droplet is given by equation (50).
\[D = 2\,R = \dfrac{2\,2\,\sigma}{\Delta P} =
\dfrac{4\times 0.0728 }{1000} \sim 2.912\,{10}^{-4} [m] \]
Example 1.20
Calculate the pressure difference between a droplet of water at \(20^{\circ}C\) when the droplet has a diameter of 0.02 cm.
Solution 1.20
using equation
\[\Delta P = \dfrac{2\,\sigma}{r} \sim
\dfrac{2\times 0.0728}{0.0002} \sim
728.0 [N/m^2] \]
Example 1.21
Calculate the maximum force necessary to lift a thin wire ring of 0.04[m] diameter from a water surface at \(20^{\circ}C\) . Neglect the weight of the ring.
Solution 1.21
\[
F = 2(2\,\pi\,r\,\sigma)\cos\beta
\]
\[
F = 4\,\pi\,r\,\sigma = 4\times \pi \times 0.04\times
0.0728 \sim .0366 [N]
\]
In this value the gravity is not accounted for.
Example 1.22
A small liquid drop is surrounded with the air and has a diameter of 0.001 [m]. The pressure difference between the inside and outside droplet is 1[kPa]. Estimate the surface tension?
Solution 1.22
To be continue
| Chemical formula | Temperature, \(T\,[^{\circ}C]\) | Surface Tension, \(\left[\dfrac{ N}{m} \right]\) | correction |
| Acetic Acid | 27.6 | 20 | n/a |
| Acetone | 25.20 | - | -0.1120 |
| Aniline | 43.4 | 22 | -0.1085 |
| Benzene | 28.88 | - | -0.1291 |
| Benzylalcohol | 39.00 | - | -0.0920 |
| Benzylbenzoate | 45.95 | - | -0.1066 |
| Bromobenzene | 36.50 | - | -0.1160 |
| Bromobenzene | 36.50 | - | -0.1160 |
| Bromoform | 41.50 | - | -0.1308 |
| Butyronitrile | 28.10 | - | -0.1037 |
| Carbon disulfid | 32.30 | - | -0.1484 |
| Quinoline | 43.12 | - | -0.1063 |
| Chloro benzene | 33.60 | - | -0.1191 |
| Chloroform | 27.50 | - | -0.1295 |
| Cyclohexane | 24.95 | - | -0.1211 |
| Cyclohexanol | 34.40 | \(25^{\circ}C\) | -0.0966 |
| Cyclopentanol | 32.70 | - | -0.1011 |
| Carbon Tetrachloride | 26.8 | - | n/a |
| Carbon disulfid | 32.30 | - | -0.1484 |
| Chlorobutane | 23.10 | - | -0.1117 |
| Ethyl Alcohol | 22.3 | - | n/a |
| Ethanol | 22.10 | - | -0.0832 |
| Ethylbenzene | 29.20 | - | -0.1094 |
| Ethylbromide | 24.20 | - | -0.1159 |
| Ethylene glycol | 47.70 | - | -0.0890 |
| Formamide | 58.20 | - | -0.0842 |
| Gasoline | - | n/a | |
| Glycerol | 64.0 | - | -0.0598 |
| Helium | 0.12 | \(-269^{\circ}C\) | n/a |
| Mercury | 425-465.0 | - | -0.2049 |
| Methanol | 22.70 | - | -0.0773 |
| Methyl naphthalene | 38.60 | - | -0.1118 |
| Methyl Alcohol | 22.6 | - | n/a |
| Neon | 5.15 | \(-247^{\circ}C\) | n/a |
| Nitrobenzene | 43.90 | - | -0.1177 |
| Olive Oil | 43.0-48.0 | - | -0.067 |
| Perfluoroheptane | 12.85 | - | -0.0972 |
| Perfluorohexane | 11.91 | - | -0.0935 |
| Perfluorooctane | 14.00 | - | -0.0902 |
| Phenylisothiocyanate | 41.50 | - | -0.1172 |
| Propanol | 23.70 | \( 25^{\circ}C\) | -0.0777 |
| Pyridine | 38.00 | - | -0.1372 |
| Pyrrol | 36.60 | - | -0.1100 |
| SAE 30 Oil | n/a | - | n/a |
| Seawater | 54-69 | - | n/a |
| Toluene | 28.4 | - | -0.1189 |
| Turpentine | 27 | - | n/a |
| Water | 72.80 | - | -0.1514 |
| o-Xylene | 30.10 | - | -0.1101 |
| m-Xylene | 28.90 | - | -0.1104 |


