8.5: The Sliding Bed Regime
- Page ID
- 29238
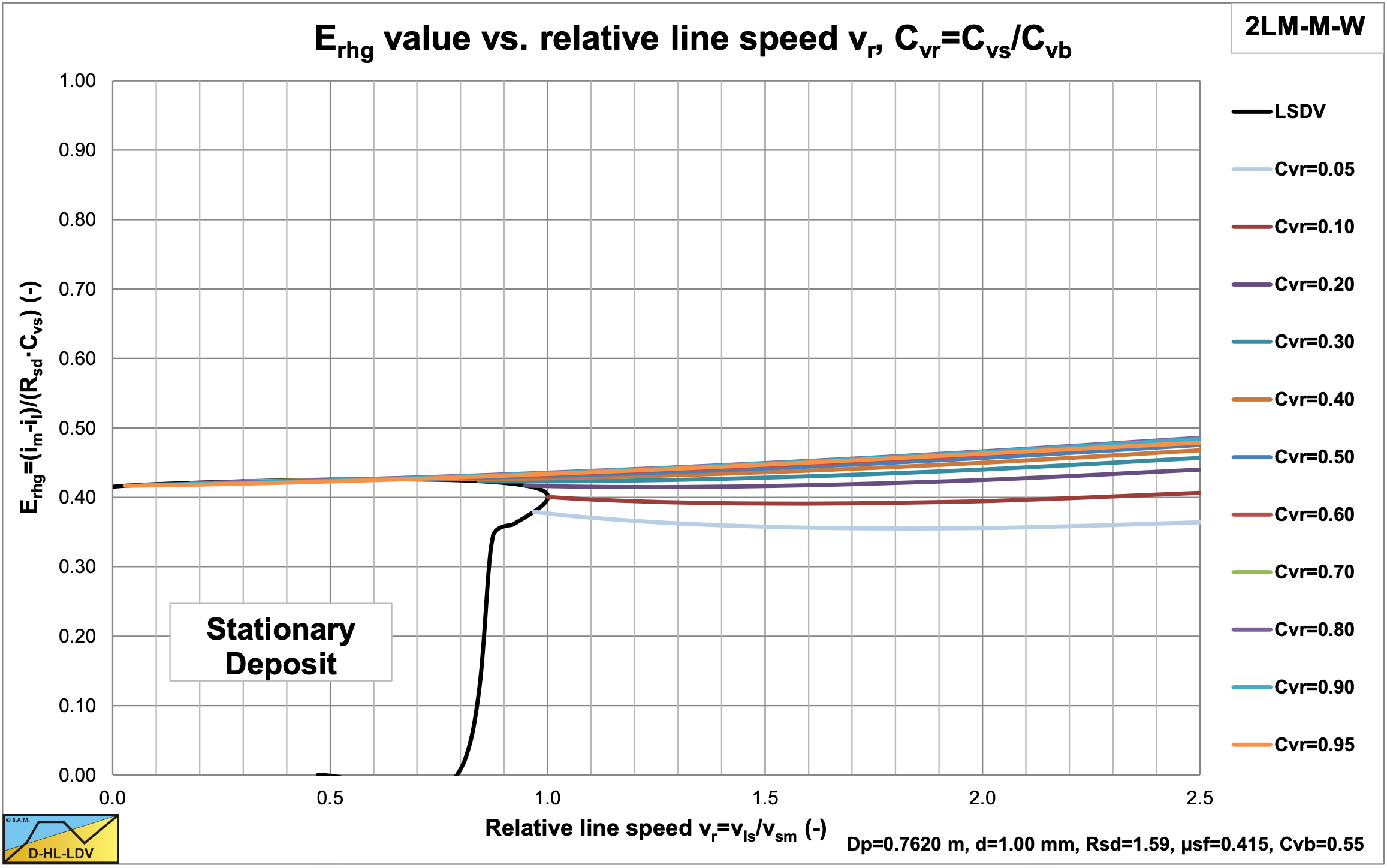
Figure 8.5-1 shows the Erhg parameter as a function of the relative volumetric concentration (Cvr=Cvs/Cb) and the relative line speed (vls/vls,ldv,max) for the weight approach sliding bed friction (Miedema & Ramsdell (2014)) and a sliding bed friction factor μsf=0.4. The Erhg parameter is very close to the sliding friction coefficient μsf, especially for relative line speeds up to 1.5, the region where most probably the sliding bed will occur. So for the sliding bed regime the Erhg parameter is defined to be equal to the sliding friction coefficient μsf. Apparently the force equilibrium on the bed is not required to determine the hydraulic gradient. For determining the bed velocity and the slip, it still is.
\[\ \mathrm{E}_{\mathrm{r h g}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v s}}}=\mu_{\mathrm{sf}}\]
The hydraulic gradient is now:
\[\ \mathrm{i}_{\mathrm{m}}=\mathrm{i}_{\mathrm{l}}+\mathrm{R}_{\mathrm{s} \mathrm{d}} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \mu_{\mathrm{s f}}\]
This gives for the pressure difference:
\[\ \Delta \mathrm{p}_{\mathrm{m}}=\Delta \mathrm{p}_{\mathrm{l}}+\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \Delta \mathrm{L} \cdot \mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \mu_{\mathrm{s f}}\]
The sliding friction coefficient μsf is the tangent of the external friction angle δ between the sand or gravel and the steel pipe wall. From soil mechanics it is known that the external friction angle δ is about 2/3 of the internal friction angle φ. This internal friction angle has a minimum of about 30° for loose packed sand, giving 20° for the external friction angle. The tangent of 20° is 0.364. Miedema & Ramsdell (2014) also analyzed the hydrostatic approach of Wilson et al. (1992) and the normal stress carrying the weight approach. These two approaches are similar up to a relative concentration of 0.5, giving an increase of the Erhg parameter with a factor 1.3 compared to the weight approach as used here. In practice the relative concentration will be between 0 and 0.5 giving a multiplication factor between 1 and 1.3 depending on the relative concentration. Taking an average gives a sliding friction factor of about 0.415. Resuming it can be stated that the Erhg parameter should have a value of about 0.364 if the weight approach is applied, or a value of about 0.415 if the hydrostatic or normal stress carrying the weight approach are applied. In the current model a constant value of 0.415 is used to be on the safe side, resulting in hydraulic gradient curves parallel to the liquid curve as already observed by Newitt et al. (1955) and others.