1.4.1: Problem Set
- Page ID
- 9483
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Write a script that will ask for pressure value in psi and display the equivalent pressure in kPa with a statement, such as "The converted pressure is: ..."
- Answer
-
% This script converts pressures from psi to kPa % User is prompted to enter pressure in psi clc % Clear screen disp('This script converts pressures from psi to kPa:') disp(' ') % Display blank line psi=input('What is the pressure value in psi? '); kPa=psi*6.894757; % Calculating pressure in kPa disp(' ') % Display blank line str = ['The converted pressure is: ', num2str(kPa), ' kPa.']; disp(str); The script output is as follows: This script converts pressures from psi to kPa: What is the pressure value in psi? 150 The converted pressure is: 1034.2135 kPa.
Write a script that generates a table of conversions from Fahrenheit to Celsius temperatures for a range and increment entered by the user, such as
Enter the beginning temperature in F:
Enter the ending temperature in F:
Enter the increment value:
Test your script with 20 the beginning Fahrenheit value, 200 the ending Fahrenheit value and 20 the increment.
- Answer
-
% This script generates a table of conversions % From Fahrenheit to Celsius temperatures clc % Clear screen disp('This script generates a table of conversions from Fahrenheit to Celsius') disp(' ') % Display blank line lowerF=input('Enter the beginning temperature in F: '); upperF=input('Enter the ending temperature in F: '); increment=input('Enter the increment value: '); Fahrenheit=[lowerF:increment:upperF]; % Creating a row vector with F values Celsius=5/9*(Fahrenheit-32); % Converting from F to C disp(' ') % Display blank line str = ['Fahrenheit Celsius '];% Displaying table header disp(str); % Tabulating results in two columns, ' is being used to transpose row to column disp([Fahrenheit' Celsius']) The script output is as follows: This script generates a table of conversions from Fahrenheit to Celsius Enter the beginning temperature in F: 20 Enter the ending temperature in F: 200 Enter the increment value: 20 Fahrenheit Celsius 20.0000 -6.6667 40.0000 4.4444 60.0000 15.5556 80.0000 26.6667 100.0000 37.7778 120.0000 48.8889 140.0000 60.0000 160.0000 71.1111 180.0000 82.2222 200.0000 93.3333
Example \(\PageIndex{1}\)
Pascal's Law states that pressure is transmitted undiminished in all directions throughout a fluid at rest. (See the illustration below). An initial force of 150 N is transmitted from a piston of 25 mm^2 to a piston of 100 mm^2. This force is progressively increased up to 200 N. Write a script that computes the corresponding load carried by the larger piston and tabulate your results.
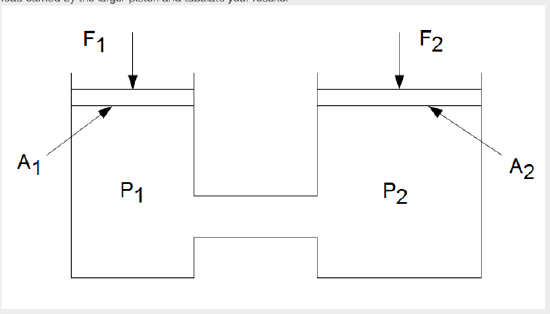
Figure \(\PageIndex{1}\). A simple hydraulic system.
- Answer
-
% This script computes the load carried by the larger piston in a hydraulic system clc % Clear screen disp('This script computes the load carried by the larger piston in a hydraulic system') disp(' ') % Display blank line initialF=150; finalF=200; increment=10; area1=25; area2=100; F1=[initialF:increment:finalF]; % Creating a row vector with F1 values F2=F1*area2/area1; % Calculating F2 values disp(' ') % Display blank line str = [' F1 F2 '];% Displaying table header disp(str); disp([F1' F2']) % Tabulating results in two columns, ' is being used to transpose row to column The script output is as follows: This script computes the load carried by the larger piston in a hydraulic system F1 F2 150 600 160 640 170 680 180 720 190 760 200 800
Example \(\PageIndex{1}\)
Modify your script in previous problem so that the user provides the following input:
Enter the initial force in N:
Enter the final force in N:
Enter the increment value:
Enter the area of small piston in mm^2:
Enter the area of big piston in mm^2:
Test your script with 150, 200, 10, 25 and 100 with respect to each input variable.
- Answer
-
% This script computes the load carried by the larger piston in a hydraulic system clc % Clear screen disp('This script computes the load carried by the larger piston in a hydraulic system') disp(' ') % Display blank line initialF=input('Enter the initial force in N: '); finalF=input('Enter the final force in N: '); increment=input('Enter the increment value: '); area1=input('Enter the area of small piston in mm^2: '); area2=input('Enter the area of big piston in mm^2: '); F1=[initialF:increment:finalF]; % Creating a row vector with F1 values F2=F1*area2/area1; % Calculating F2 values disp(' ') % Display blank line str = [' F1 F2 '];% Displaying table header disp(str); disp([F1' F2']) % Tabulating results in two columns, ' is being used to transpose row to column The script output is as follows: This script computes the load carried by the larger piston in a hydraulic system Enter the initial force in N: 150 Enter the final force in N: 200 Enter the increment value: 10 Enter the area of small piston in mm^2: 25 Enter the area of big piston in mm^2: 100 F1 F2 150 600 160 640 170 680 180 720 190 760 200 800
Write a script to solve the Stress-Strain problem in the Problem Set
- Answer
-
The m-file contains the following:
% This script uses readings from a Tensile test and % Computes Strain and Stress values clc % Clear screen disp('This script uses readings from a Tensile test and') disp('Computes Strain and Stress values') disp(' ') % Display a blank line Specimen_dia=12.7; % Specimen diameter in mm % Load in kN Load_kN=[0;4.89;9.779;14.67;19.56;24.45;... 27.62;29.39;32.68;33.95;34.58;35.22;... 35.72;40.54;48.39;59.03;65.87;69.42;... 69.67;68.15;60.81]; % Gage length in mm Length_mm=[50.8;50.8102;50.8203;50.8305;... 50.8406;50.8508;50.8610;50.8711;... 50.9016;50.9270;50.9524;50.9778;... 51.0032;51.816;53.340;55.880;58.420;... 60.96;61.468;63.5;66.04]; % Calculate x-sectional area im m2 Cross_sectional_Area=pi/4*((Specimen_dia/1000)^2); % Calculate change in length, initial lenght is 50.8 mm Delta_L=Length_mm-50.8; % Calculate Stress in MPa Sigma=(Load_kN./Cross_sectional_Area)*10^(-3); % Calculate Strain in mm/mm Epsilon=Delta_L./50.8; str = ['Specimen diameter is ', num2str(Specimen_dia), ' mm.']; disp(str); Results=[Load_kN Length_mm Delta_L Sigma Epsilon]; % Tabulated results disp(' Load Length Delta L Stress Strain') disp(Results)After executed, the command window output is:
This script uses readings from a Tensile test and Computes Strain and Stress values Specimen diameter is 12.7 mm. Load Length Delta L Stress Strain 0 50.8000 0 0 0 4.8900 50.8102 0.0102 38.6022 0.0002 9.7790 50.8203 0.0203 77.1964 0.0004 14.6700 50.8305 0.0305 115.8065 0.0006 19.5600 50.8406 0.0406 154.4086 0.0008 24.4500 50.8508 0.0508 193.0108 0.0010 27.6200 50.8610 0.0610 218.0351 0.0012 29.3900 50.8711 0.0711 232.0076 0.0014 32.6800 50.9016 0.1016 257.9792 0.0020 33.9500 50.9270 0.1270 268.0047 0.0025 34.5800 50.9524 0.1524 272.9780 0.0030 35.2200 50.9778 0.1778 278.0302 0.0035 35.7200 51.0032 0.2032 281.9773 0.0040 40.5400 51.8160 1.0160 320.0269 0.0200 48.3900 53.3400 2.5400 381.9955 0.0500 59.0300 55.8800 5.0800 465.9888 0.1000 65.8700 58.4200 7.6200 519.9844 0.1500 69.4200 60.9600 10.1600 548.0085 0.2000 69.6700 61.4680 10.6680 549.9820 0.2100 68.1500 63.5000 12.7000 537.9830 0.2500 60.8100 66.0400 15.2400 480.0403 0.3000
Example \(\PageIndex{1}\)
Modify the script, you wrote above and plot an annotated Stress-Strain graph.
- Answer
-
Edited script contains the plot commands: % This script uses readings from a Tensile test and % Computes Strain and Stress values clc % Clear screen disp('This script uses readings from a Tensile test and') disp('Computes Strain and Stress values') disp(' ') % Display a blank line Specimen_dia=12.7; % Specimen diameter in mm % Load in kN Load_kN= [0;4.89;9.779;14.67;19.56;24.45;...27.62;29.39;32.68;33.95;34.58;35.22;...35.72;40.54;48.39;59.03;65.87;69.42;... 69.67;68.15;60.81];% Gage length in mm Length_mm=[50.8;50.8102;50.8203;50.8305;...50.8406;50.8508;50.8610;50.8711;...50.9016;50.9270;50.9524;50.9778;... 51.0032;51.816;53.340;55.880;58.420;... 60.96;61.468;63.5;66.04]; % Calculate x-sectional area im m2 Cross_sectional_Area=pi/4*((Specimen_dia/1000)^2); % Calculate change in length, initial lenght is 50.8 mm
Delta_L=Length_mm-50.8; % Calculate Stress in MPa Sigma=
(Load_kN./Cross_sectional_Area)*10^(-3); % Calculate Strain in mm/mm
Epsilon=Delta_L./50.8; str = ['Specimen diameter is ', num2str(Specimen_dia), ' mm.'];
disp(str); Results=[Load_kN Length_mm Delta_L Sigma Epsilon]; % Tabulated results
disp(' Load Length Delta L Stress Strain') disp(Results) % Plot Stress versus Strain
plot(Epsilon,Sigma) title('Stress versus Strain Curve') xlabel('Strain [mm/mm]')
ylabel('Stress [mPa]') grid In addition to Command Window output, the following plot is generated:
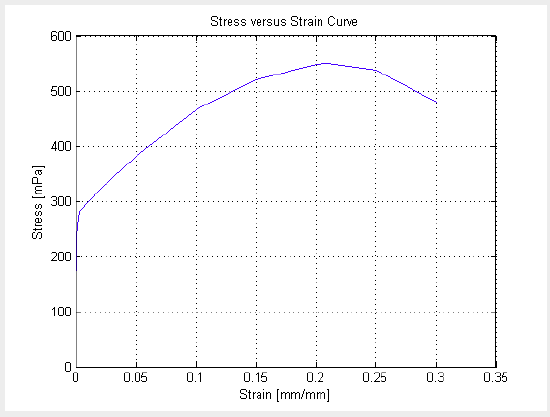
Repeat Problem 2, this time using a combination of disp, fprintf commands and a for loop.
- Answer
-
The re-worked solution:
% This script generates a table of conversions % From Fahrenheit to Celsius temperatures clear % removes all variables from the current workspace, clc % clears all input and output from the Command Window display, disp('This script generates a table of conversions from Fahrenheit to Celsius') disp(' ') % Display blank line lowerF=input('Enter the initial temperature in F: '); upperF=input('Enter the final temperature in F: '); increment=input('Enter the increment value: '); disp(' ') % Display blank line fprintf('Fahrenheit Celsius\n') % title row fprintf('------------------\n') % title row for Fahrenheit=[lowerF:increment:upperF]; % Creating a row vector with F values Celsius=5/9*(Fahrenheit-32); % Converting from F to C fprintf('%8.3f %8.3f \n',Fahrenheit,Celsius); % Tabulating results in two columns end
After executed, the command window output is:
This script generates a table of conversions from Fahrenheit to Celsius Enter the initial temperature in F: 20 Enter the final temperature in F: 200 Enter the increment value: 20 Fahrenheit Celsius ------------------ 20.000 -6.667 40.000 4.444 60.000 15.556 80.000 26.667 100.000 37.778 120.000 48.889 140.000 60.000 160.000 71.111 180.000 82.222 200.000 93.333
Repeat Problem 7, this time using a while loop.
- Answer
-
The re-worked solution:
% This script generates a table of conversions % From Fahrenheit to Celsius temperatures clear % removes all variables from the current workspace, clc % clears all input and output from the Command Window display, disp('This script generates a table of conversions from Fahrenheit to Celsius') disp(' ') % Display blank line lowerF=input('Enter the initial temperature in F: '); upperF=input('Enter the final temperature in F: '); increment=input('Enter the increment value: '); disp(' ') %
Display blank line fprintf('Fahrenheit Celsius\n') % title row fprintf('------------------\n') % title row Fahrenheit=lowerF; while Fahrenheit<=upperF Celsius=5/9*(Fahrenheit-32);
% Converting from F to C fprintf('%8.3f %8.3f \n',Fahrenheit,Celsius); % Tabulating results in two columns Fahrenheit=Fahrenheit+increment;end
After executed, the command window output is: This script generates a table of conversions from Fahrenheit to Celsius Enter the initial temperature in F: 20 Enter the final temperature in F: 200 Enter the increment value: 20 Fahrenheit Celsius ------------------ 20.000 -6.667 40.000 4.444 60.000 15.556 80.000 26.667 100.000 37.778 120.000 48.889 140.000 60.000 160.000 71.111 180.000 82.222 200.000 93.333


