3.1: Basic Concepts
- Page ID
- 9679
A set is a collection of elements. A set is defined entirely by the elements that it contains. An element can be anything, including another set. You will notice that this is not a precise mathematical definition. Instead, it is an intuitive description of what the word ‘set’ is supposed to mean: any time you have a bunch of entities and you consider them as a unit, you have a set. Mathematically, sets are really defined by the operations that can be performed on them. These operations model things that can be done with collections of objects in the real world. These operations are the subject of the branch of mathematics known as set theory.
The most basic operation in set theory is forming a set from a given list of specific entities. The set that is formed in this way is denoted by enclosing the list of entities between a left brace, ‘{’, and a right brace, ‘}’. The entities in the list are separated by commas. For example, the set denoted by
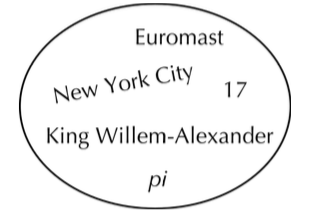
{ 17, \(\pi\), New York City, King Willem-Alexander, Euromast }
is the set that contains the entities 17, \(\pi\), New York City, King Willem-Alexander, and Euromast. These entities are the elements of the set. Since we assume that a set is completely defined by the elements that it contains, the set is well-defined. Of course, we still haven’t said what it means to be an ‘entity’. Something as definite as ‘New York City’ should qualify, except that it doesn’t seem like New York City really belongs in the world of mathematics. The problem is that mathematics is supposed to be its own self-contained world, but it is supposed to model the real world. When we use mathematics to model the real world, we admit entities such as New York City and even Euromast. But when we are doing mathematics per se, we’ll generally stick to obviously mathematical entities such as the integer 17 or the real number \(\pi\). We will also use letters such as a and b to refer to entities. For example, when I say something like “Let A be the set{a, b, c}”, I mean a, b, and c to be particular, but unspecified, entities.
It’s important to understand that a set is defined by the elements that it con- tains, and not by the order in which those elements might be listed. For example, the notations {a, b, c, d} and {b, c, a, d} define the same set. Further- more, a set can only contain one copy of a given element, even if the notation that specifies the set lists the element twice. This means that {a, b, a, a, b, c, a}and {a, b, c} specify exactly the same set. Note in particular that it’s incorrect to say that the set {a, b, a, a, b, c, a} contains seven elements, since some of the elements in the list are identical. The notation {a, b, c} can lead to some confusion, since it might not be clear whether the letters a, b, and c are as- sumed to refer to three different entities. A mathematician would generallynot make this assumption without stating it explicitly, so that the set denoted by {a, b, c} could actually contain either one, two, or three elements. When it is important that different letters refer to different entities, I will say so explicitly, as in “Consider the set {a, b, c}, where a, b, and c are distinct.”


