3.1.3: Operations on sets
- Page ID
- 10175
Now that we have a way to express a wide variety of sets, we turn to operations that can be performed on sets. The most basic operations on sets are union and intersection. IfA and B are sets, then we define the union of A and B to be the set that contains all the elements of A together with all the elements of B. The union of A and B is denoted byA ∪ B. The union can be defined formally as
\(A \cup B=\{x | x \in A \vee x \in B\}\)
The intersection of A and B is defined to be the set that contains every entity that is both a member of A and a member of B. The intersection of A and B is denoted by A∩B. Formally,
\(A \cap B=\{x | x \in A \wedge x \in B\}\)
An entity gets into A ∪ B if it is in either A or B. It gets into A ∩ B if it is in both A and B. Note that the symbol for the logical ‘or’ operator, ∨, is similar to the symbol for the union operator, ∪, while the logical ‘and’ operator, ∧, is similar to the intersection operator, ∩.
The set difference of two sets, A and B, is defined to be the set of all entities that are members of A but are not members of B. The set difference of A and B is denoted A ∖ B or alternatively as A − B. The idea is that A ∖ B is formed by starting with A and then removing any element that is also found in B. Formally,
\(A>B=\{x | x \in A \wedge x \notin B\}\)
Union and intersection are clearly commutative operations. That is, A ∪ B = B ∪ A andA ∩ B = B ∩ A for any sets A and B. However, set difference is not commutative. In general, A∖B \(\neq\) B∖A.
Suppose that \(A=\{a, b, c\}\), that \(B=\{b, d\},\) and that \(C=\{d, e, f\} .\) Then we can apply the definitions of union, intersection, and set difference to compute, for example, that:
A∪B = {a,b,c,d} A∩B = {b} A∖B = {a,c}
A∪C = {a,b,c,d,e, f} A∩C = ∅ A∖C = {a,b,c}
In this example, the sets A and C have no elements in common, so that A ∩ C = ∅. There is a term for this: Two sets are said to be disjoint if they have no elements in common. That is, for any sets A and B, A and B are said to be disjoint if and only if A ∩ B = ∅.
Of course, the set operations can also be applied to sets that are defined by predicates. The next example illustrates this.
let L(x) be the predicate ‘x is lucky’, and let W(x) be the predicate ‘x is wise’, where the domain of discourse for each predicate is the set of people. LetX = {x | L(x)}, and let Y = {x | W(x)}. Then
X ∪ Y = {x | L(x) ∨ W(x)} = {people who are lucky or wise}
X ∩ Y = {x | L(x) ∧ W(x)} = {people who are lucky and wise}
X ∖ Y = {x | L(x) ∧ ¬W(x)} = {people who are lucky but not wise}
Y ∖ X = {x | W(x) ∧ ¬L(x)} = {people who are wise but not lucky}
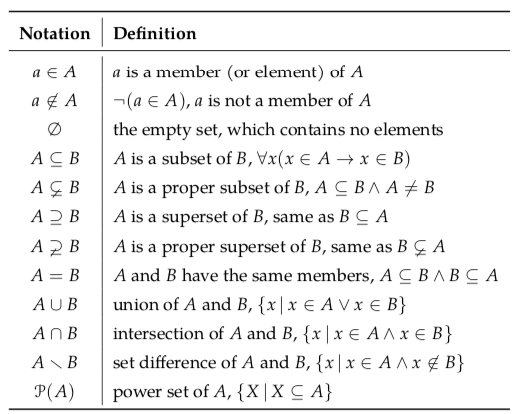
Figure 4.2: Some of the notations that are defined in this section. A and B are sets, anda is an entity.
You have to be a little careful with the English word ‘and’. We might say that the set X ∪ Y contains people who are lucky and people who are wise. But what this means is that a person gets into the set X ∪ Y either by being lucky or by being wise, so X ∪ Y is defined using the logical ‘or’ operator, ∨.

