4.5: Non-context-free Languages
- Page ID
- 6733
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We have seen that there are context-free languages that are not regular. The natural question arises, are there languages that are not context-free? It’s easy to answer this question in the abstract: For a given alphabet Σ, there are uncountably many languages over Σ, but there are only countably many context-free languages over Σ. It follows that most languages are not context-free. However, this answer is not very satisfying since it doesn’t give us any example of a specific language that is not context-free.
As in the case of regular languages, one way to show that a given lan- guage L is not context-free is to find some property that is shared by all context-free languages and then to show that L does not have that prop- erty. For regular languages, the Pumping Lemma gave us such a property. It turns out that there is a similar Pumping Lemma for context-free lan- guages. The proof of this lemma uses parse trees. In the proof, we will need a way of representing abstract parse trees, without showing all the details of the tree. The picture
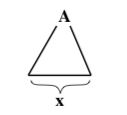
represents a parse tree which has the non-terminal symbol A at its root and the string x along the “bottom” of the tree. (That is, x is the string made up of all the symbols at the endpoints of the tree’s branches, read from left to right.) Note that this could be a partial parse tree—something that could be a part of a larger tree. That is, we do not require A to be the start symbol of the grammar and we allow x to contain both terminal and non-terminal symbols. The string x, which is along the bottom of the tree, is referred to as the yield of the parse tree. Sometimes, we need to show more explicit detail in the tree. For example, the picture
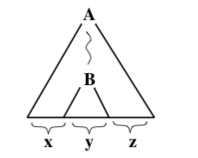
represents a parse tree in which the yield is the string xyz. The string y is the yield of a smaller tree, with root B, which is contained within the larger tree. Note that any of the strings x, y, or z could be the empty string.
We will also need the concept of the height of a parse tree. The height of a parse tree is the length of the longest path from the root of the tree to the tip of one of its branches.
Like the version for regular languages, the Pumping Lemma for context- free languages shows that any sufficiently long string in a context-free language contains a pattern that can be repeated to produce new strings that are also in the language. However, the pattern in this case is more complicated. For regular languages, the pattern arises because any sufficiently long path through a given DFA must contain a loop. For context-free languages, the pattern arises because in a sufficiently large parse tree, along a path from the root of the tree to the tip of one of its branches, there must be some non-terminal symbol that occurs more than once.
Theorem 4.7
(Pumping Lemma for Context-free Languages). Suppose that L is a context-free language. Then there is an integer K such that any string \(w \in L(G)\) with \(|w| \geq K\) has the property that w can be written in the form w = uxyzv where
- x and z are not both equal to the empty string;
- |xyz| < K; and
- For any \(n \in \mathbb{N},\) the string \(u x^{n} y z^{n} v\) is in \(L\)
Proof. Let \(G=(V, \Sigma, P, S)\) be a context-free grammar for the languageL. Let N be the number of non-terminal symbols in G, plus 1. That is, \(N=|V|+1\). Consider all possible parse trees for the grammar G with height less than or equal to N. (Include parse trees with any non-terminal symbol as root, not just parse trees with root S.) There are only finitely many such parse trees, and therefore there are only finitely many different strings that are the yields of such parse trees. Let K be an integer which is greater than the length of any such string.
Now suppose that w is any string in L whose length is greater than or equal to K. Then any parse tree for w must have height greater than N. (This follows since \(|w| \geq K\) and the yield of any parse tree of height \(\leq N\) has length less than \(K\). Consider a parse tree for w of minimal size, that is one that contains the smallest possible number of nodes. Since the height of this parse tree is greater than N, there is at least one path from the root of the tree to tip of a branch of the tree that has length greater than N. Consider the longest such path. The symbol at the tip of this path is a terminal symbol, but all the other symbols on the path are non- terminal symbols. There are at least N such non-terminal symbols on the path. Since the number of different non-terminal symbols is |V | and since \(N=|V|+1\), some non-terminal symbol must occur twice on the path. In fact, some non-terminal symbol must occur twice among the bottommostN non-terminal symbols on the path. Call this symbol A. Then we see that the parse tree for w has the form shown here:
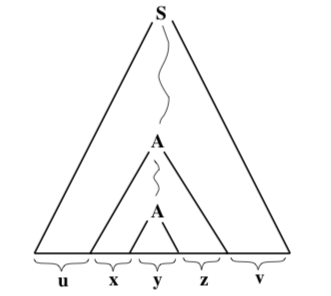
The structure of this tree breaks the string w into five substrings, as shown in the above diagram. We then have w = uxyzv. It only remains to show that x, y, and z satisfy the three requirements stated in the theorem.
Let T refer to the entire parse tree, let \(T_{1}\) refer to the parse tree whose root is the upper A in the diagram, and let \(T_{2}\) be the parse tree whose root is the lower A in the diagram. Note that the height of is \(T_{1}\) less than or equal to N. (This follows from two facts: The path shown in T1 from its root to its base has length less than or equal to N, because we chose the two occurrences of A to be among the N bottommost non-terminal symbols along the path in T from its root to its base. We know that there is no longer path from the root of T1 to its base, since we chose the path in Tto be the longest possible path from the root of T to its base.) Since any parse tree with height less than or equal to N has yield of length less than \(K,\) we see that \(|x y z|<K\).
If we remove \(T_{1}\) from T and replace it with a copy of \(T_{2}\), the result is a parse tree with yield uyv, so we see that the string uyv is in the language L. Now, suppose that both x and z are equal to the empty string. In that case, w = uyv, so the tree we have created would be another parse tree for w. But this tree is smaller than T, so this would contradict the fact that T is the smallest parse tree for w. We see that x and z cannot both be the empty string.
If we remove \(T_{2}\) from T and replace it with a copy of \(T_{1}\), the result is a parse tree with yield \(u x^{2} y z^{2} v,\) so we see that \(u x^{2} y z^{2} v \in L .\) The two parse trees that we have created look like this:
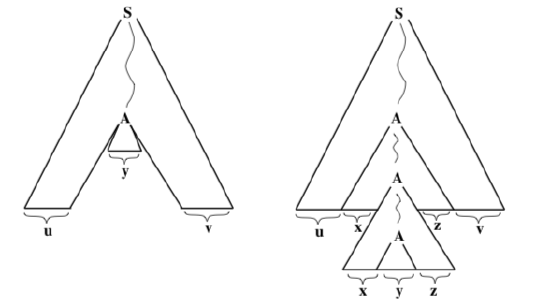
Furthermore, we can apply the process of replacing \(T_{2}\) with a copy of \(T_{1}\) to the tree on the right above to create a parse tree with yield \(u x^{3} y z^{3} v\). Continuing in this way, we see that \(u x^{n} y z^{n} v \in L\) for all \(n \in \mathbb{N}\). This completes the proof of the theorem.
Since this theorem guarantees that all context-free languages have a certain property, it can be used to show that specific languages are not context-free. The method is to show that the language in question does not have the property that is guaranteed by the theorem. We give two examples.
Corollary 4.8.
Let L be the language \(\left\{a^{n} b^{n} c^{n} | n \in \mathbb{N}\right\}\). Then L is not a context-free language.
Proof. We give a proof by contradiction. Suppose that L is context-free. Then, by the Pumping Lemma for Context-free Languages, there is an integer \(K\) such that every string \(w \in L\) with \(|w| \geq K\) can be written in the form \(w=u x y z v\) where \(x\) and \(z\) are not both empty, \(|x y z|<K,\) and \(u x^{n} y z^{n} v \in L\) for every \(n \in \mathbb{N}\).
Consider the string \(w=a^{K} b^{K} c^{K},\) which is in \(L,\) and write \(w=u x y z v\), where u, x, y, z, and v satisfy the stated conditions. Since \(|x y z|<K\) we see that if xyz contains an a, then it cannot contain a c. And if it contains a c, then it cannot contain an a. It is also possible that xyz is made up entirely of \(b^{\prime} s .\) In any of these cases, the string \(u x^{2} y z^{2} v\) cannot be in L, since it does not contain equal numbers of a’s, b’s, and c’s. But this contradicts the fact that \(u x^{n} y z^{n} v \in L\) for all \(n \in \mathbb{N} .\) This contradiction shows that the assumption that L is context-free is incorrect.
Corollary 4.9.
Let Σ be any alphabet that contains at least two symbols. Let L be the language over Σ defined by \(L=\left\{s s | s \in \Sigma^{*}\right\}\). Then L is not context-free.
Proof. Suppose, for the sake of contradiction, that L is context-free. Then, by the Pumping Lemma for Context-free Languages, there is an integer \(K\) such that every string \(w \in L\) with \(|w| \geq K\) can be written in the form \(w=u x y z v\) where \(x\) and \(z\) are not both empty, \(|x y z|<K,\) and \(u x^{n} y z^{n} v \in L\) for every \(n \in \mathbb{N}\).
Let \(a\) and \(b\) represent distinct symbols in \(\Sigma .\) Let \(s=a^{K} b a^{K} b\) and let \(w=s s=a^{K} b a^{K} b a^{K} b a^{K} b,\) which is in \(L .\) Write \(w=u x y z v,\) where \(u, x, y\) z, and v satisfy the stated conditions.
Since \(|x y z|<K, x\) and \(z\) can, together, contain no more than one \(b\). If either \(x\) or \(y\) contains a \(b,\) then \(u x^{2} y z^{2} v\) contains exactly five \(b\) 's. But any string in L is of the form rr for some string r and so contains an even number of \(b^{\prime} s .\) The fact that \(u x^{2} y z^{2} z\) contains five \(b^{\prime}\) s contradicts the fact that \(u x^{2} y z^{2} v \in L .\) So, we get a contradiction in the case where \(x\) or \(y\) contains a b.
Now, consider the case where x and y consist entirely of a’s. Again since \(|x y z|<K,\) we must have either that \(x\) and \(y\) are both contained in the same group of \(a^{\prime} s\) in the string \(a^{K} b a^{K} b a^{K} b a^{K} b,\) or that \(x\) is contained in one group of a’s and y is contained in the next. In either case, it is easy to check that the string \(u x^{2} y z^{2} v\) is no longer of the form \(r r\) for any string \(r,\) which contradicts the fact that \(u x^{2} y z^{2} v \in L\).
Since we are led to a contradiction in every case, we see that the as- sumption that L is context-free must be incorrect.
Now that we have some examples of languages that are not context- free, we can settle some other questions about context-free languages. In particular, we can show that the intersection of two context-free languages is not necessarily context-free and that the complement of a context-free language is not necessarily context-free.
Theorem 4.10.
The intersection of two context-free languages is not nec- essarily a context-free language.
Proof. To prove this, it is only necessary to produce an example of two context-free languages \(L\) and \(M\) such that \(L \cap M\) is not a context-free languages. Consider the following languages, defined over the alphabet \(\Sigma=\{a, b, c\}\):
\(L=\left\{a^{n} b^{n} c^{m} | n \in \mathbb{N} \text { and } m \in \mathbb{N}\right\}\)
\(M=\left\{a^{n} b^{m} c^{m} | n \in \mathbb{N} \text { and } m \in \mathbb{N}\right\}\)
Note that strings in L have equal numbers of a’s and b’s while strings in \(M\) have equal numbers of \(b^{\prime} s\) and \(c^{\prime} s .\) It follows that strings in \(L \cap M\) have equal numbers of a’s, b’s, and c’s. That is,
\(L \cap M=\left\{a^{n} b^{n} c^{n} | n \in \mathbb{N}\right\}\)
We know from the above theorem that \(L \cap M\) is not context-free. However, both L and M are context-free. The language L is generated by the context- free grammar
\(S \longrightarrow T C\)
\(C \longrightarrow c C\)
\(C \longrightarrow \varepsilon\)
\(T \longrightarrow a T b\)
\(T \longrightarrow \varepsilon\)
and M is generated by a similar context-free grammar.
Corollary 4.11.
The complement of a context-free language is not necessarily context-free.
Proof. Suppose for the sake of contradiction that the complement of every context-free language is context-free.
Let L and M be two context-free languages over the alphabet Σ. By our assumption, the complements \(\overline{L}\) and \(\overline{M}\) are context-free. By Theorem 4.3, it follows that \(\overline{L} \cup \vec{M}\) is context-free. Applying our assumption once again, we have that \(\overline{\overline{L} \cup \overline{M}}\) is context-free. But \(\overline{\overline{L}} \cup \overline{M}=L \cap M,\) so we have that \(L \cap M\) is context-free.
We have shown, based on our assumption that the complement of any context-free language is context-free, that the intersection of any two context- free languages is context-free. But this contradicts the previous theorem, so we see that the assumption cannot be true. This proves the theorem.
Note that the preceding theorem and corollary say only that \(L \cap M\) is not context-free for some context-free languages \(L\) and \(M\) and that \(\overline{L}\) is not context-free for some context-free language L. There are, of course, many examples of context-free languages \(L\) and \(M\) for which \(L \cap M\) and \(\overline{L}\) are in fact context-free.
Even though the intersection of two context-free languages is not necessarily context-free, it happens that the intersection of a context-free language with a regular language is always context-free. This is not difficult to show, and a proof is outlined in Exercise 4.4.8. I state it here without proof:
Theorem 4.12.
Suppose that L is a context-free language and that M is a regular language. Then \(L \cap M\) is a context-free language.
For example, let L and M be the languages defined by \(L=\{w \in\)\(\{a, b\}^{*} | w=w^{R} \}\) and \(M=\left\{w \in\{a, b\}^{*} | \text { the length of } w \text { is a multiple }\right.\)of 5\(\} .\) since \(L\) is context-free and \(M\) is regular, we know that \(L \cap M\) is context-free. The language \(L \cap M\) consists of every palindrome over the alphabet \(\{a, b\}\) whose length is a multiple of five.
This theorem can also be used to show that certain languages are not context-free. For example, consider the language \(L=\left\{w \in\{a, b, c\}^{*} | n_{a}(w)\right.\)\(=n_{b}(w)=n_{c}(w) \} .\) (Recall that \(n_{x}(w)\) is the number of times that the symbol x occurs in the string w.) We can use a proof by contradiction to show that L is not context-free. Let M be the regular language defined by the regular expression \(a^{*} b^{*} c^{*} .\) It is clear that \(L \cap M=\left\{a^{n} b^{n} c^{n} | n \in \mathbb{N}\right\} .\) If \(L\) were context-free, then, by the previous theorem, \(L \cap M\) would be context-free. However, we know from Theorem 4.8 that \(L \cap M\) is not context-free. So we can conclude that L is not context-free.
Exercises
- Show that the following languages are not context-free:
a) \(\left\{a^{n} b^{m} c^{k} | n>m>k\right\}\)
b) \(\left\{w \in\{a, b, c\}^{*} | n_{a}(w)>n_{b}(w)>n_{c}(w)\right\}\)
c) \(\left\{w w w | w \in\{a, b\}^{*}\right\}\)
d) \(\left\{a^{n} b^{m} c^{k} | n, m \in \mathbb{N} \text { and } k=m * n\right\}\)
e) \(\left\{a^{n} b^{m} | m=n^{2}\right\}\)
2. Show that the languages \(\left\{a^{n} | \mathrm{n} \text { is a prime number }\right\}\) and \(\left\{a^{n^{2}} | n \in \mathbb{N}\right\}\) are not context-free. (In fact, it can be shown that a language over the alphabet{a} is context-free if and only if it is regular.)
3. Show that the language \(\left\{w \in\{a, b\}^{*} | n_{a}(w)=n_{b}(w) \text { and } w \text { contains the }\right.\) string baaab as a substring} is context-free.
4. Suppose that M is any finite language and that L is any context-free language. Show that the language L \ M is context-free. (Hint: Any finite language is a regular language.)


