4.4: Reasoning Services
- Page ID
- 6417
The reasoning services for DLs can be divided into so-called ‘standard’ reasoning services and ‘non-standard’ reasoning services. The former are more common and provided by all extant DL reasoners, whereas for the latter, new problems had been defined that needed specific algorithms, extensions, and interfaces to the standard ones. In this section, only the standard ones are considered; an example example of the latter is deferred to Section 7.5, because the ‘non-standard’ ones are typically focused on assisting modelers in the ontology authoring process, rather than purely deriving knowledge only.
Standard Reasoning Services
Recalling the four essential components of (automated) reasoning listed in 2.2: Reasoning, the formal language in this case is a DL, and we take a closer look the choice of class of problems the software has to solve. The standard reasoning services are as follows, i.e., generally, all DL-focused automated reasoners offer these services.
- Consistency of the knowledge base \((\mathcal{KB}\nvDash\top\sqsubseteq\bot )\)
- Is the \(\mathcal{KB}=(\mathcal{T},\mathcal{A})\) consistent (non-selfcontradictory), i.e., is there at least one model for \(\mathcal{KB}\), i.e.: “can all concepts and roles be instantiated without leading to a contradiction?”
- Concept (and role) satisfiability \((\mathcal{KB}\nvDash C\sqsubseteq\bot )\)
- is there a model of \(\mathcal{KB}\) in which \(C\) (resp. \(R\)) has a nonempty extension, i.e., “can that concept (role) have instances without leading to contradictions?”
- Concept (and role) subsumption \((\mathcal{KB}\models C\sqsubseteq D)\)
- i.e., is the extension of \(C\) (resp. \(R\)) contained in the extension of \(D\) (resp. \(S\)) in every model of \(\mathcal{T}\) (the TBox), i.e., ‘are all instances of \(C\) also instances of \(D\)?
- Instance checking \((\mathcal{KB}\models C(a)\) or \(\mathcal{KB}\models R(a,b))\)
- is a (resp. \((a, b))\) a member of concept \(C\) (resp. \(R\)) in \(\mathcal{KB}\), i.e., is the fact \(C(a)\) (resp. \(R(a, b))\) satisfied by every interpretation of \(\mathcal{KB}\)?
- Instance retrieval \((\{ a|\mathcal{KB}\models C(a)\} )\)
- find all members of \(C\) in \(\mathcal{KB}\), i.e., compute all individuals \(a\) s.t. \(C(a)\) is satisfied by every interpretation of \(\mathcal{KB}\)
You have used the underlying idea of concept subsumption both with EER and UML class diagrams, but then you did it all manually, like declaring that all cars are vehicles. Now, instead of you having to model a hierarchy of entity types/classes, we let the automated reasoner compute it for us thanks to the properties that have been represented for the DL concepts.
The following two examples illustrate logical implication and concept subsumption.
Example Logical implication \(\PageIndex{1}\):
Consider logical implication—i.e., \(\mathcal{KB}\models\phi\) if every model of \(\mathcal{KB}\) is a model of \(\phi\)—with the following example:
- TBox: \(\exists\texttt{teaches.Course}\sqsubseteq\neg\texttt{Undergrad}\sqcup\texttt{Professor}\)
“The objects that teaches a course are not undergrads or professors”
- ABox: \(\texttt{teaches(Thembi, cs101)}\), \(\texttt{Course(cs101)}\), \(\texttt{Undergrad(Thembi)}\)
This is depicted graphically in Figure 3.3.1. What does it entail, if anything? The only possibility to keep this logical theory consistent and satisfiable is to infer that Thembi is a professor, i.e., \(\mathcal{KB}\models\texttt{Professor(Thembi)}\), because anything that teaches a course must be either not an undergrad or a professor. Given that Thembi is an undergrad, she cannot be not an undergrad, hence, she has to be a professor.
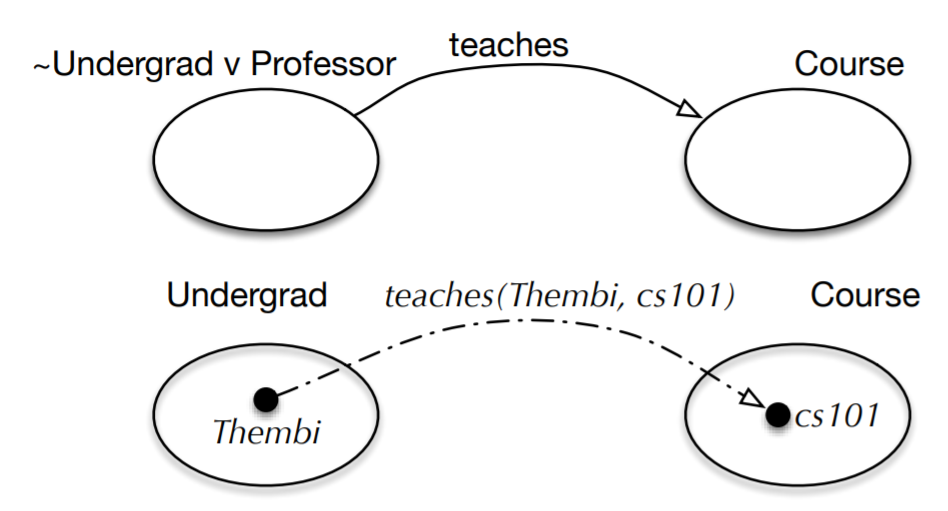.png?revision=1&size=bestfit&width=738&height=398)
Figure 3.3.1: Top: Depiction of the TBox according to the given axiom; bottom: depiction of the ABox. See Example 3.3.1 for details.
What will happen if we have the following knowledge base?
- TBox: \(\exists\texttt{teaches.Course}\sqsubseteq\texttt{Undergrad}\sqcup\texttt{Professor}\)
- ABox: \(\texttt{teaches(Thembi, cs101)}\), \(\texttt{Course(cs101)}\), \(\texttt{Undergrad(Thembi)}\)
That is, do we obtain \(\mathcal{KB}\models\texttt{Professor(Thembi)}\) again? No.
Perhaps the opposite, that \(\mathcal{KB}\models\neg\texttt{Professor(Thembi)}\)? No. Can you explain why?
Example Concept subsumption \(\PageIndex{2}\):
As an example of concept subsumption, consider the knowledge base \(\mathcal{KB}\) that contains the following axioms and is depicted graphically in Figure 3.3.2 (for intuitive purpose only):
- \(\texttt{HonsStudent}\equiv\texttt{Student}\sqcap\exists\texttt{enrolled.BScHonsDegree}\)
- \(\texttt{X}\equiv\texttt{Student}\sqcap\exists\texttt{enrolled.BScHonsDegree}\sqcap\exists\texttt{hasDuty.TeachingAssistantShip}\)
- \(\texttt{Y}\equiv\texttt{Student}\sqcap\exists\texttt{enrolled.BScHonsDegree}\sqcap\exists\texttt{hasDuty.ProgrammingTask}\)
- \(\texttt{X(John)}\), \(\texttt{BScHonsDegree(comp4)}\), \(\texttt{TeachingAssistantShip(cs101)}\), \(\texttt{enrolled(John,comp4)}\), \(\texttt{hasDuty(John, cs101)}\), \(\texttt{BScHonsDegree(maths4)}\).
\(\mathcal{KB}\models\texttt{X}\sqsubseteq\texttt{HonsStudent}\)? That is, is the extension of X contained in the extension of HonsStudent in every model of \(\mathcal{KB}\)? Yes. Why? We know that both HonsStudent and X are subclasses of Student and that both are enrolled in an BScHonsDegree programme. In addition, every instance of X also has a duty performing a TeachingAssistantShip for an undergrad module, whereas, possibly, not all honours students work as a teaching assistant. Thus, all X’s are always also an instance of HonsStudent in every possible model of \(\mathcal{KB}\), hence \(\mathcal{KB}\models\texttt{X}\sqsubseteq\texttt{HonsStudent}\). And likewise for \(\mathcal{KB}\models\texttt{Y}\sqsubseteq\texttt{HonsStudent}\). This deduction is depicted in green in Figure 3.3.3.
Let us modify this a bit by adding the following two axioms to \(\mathcal{KB}\):
- \(\texttt{Z}\equiv\texttt{Student}\sqcap\exists\texttt{enrolled.BScHonsDegree}\sqcap\exists\texttt{hasDuty.(ProgrammingTask}\sqcap\texttt{TeachingAssistantShip)}\)
- \(\texttt{TeachingAssistantShip}\sqsubseteq\neg\texttt{ProgrammingTask}\)
What happens now? The first step is to look at Z: it has the same properties as HonsStudent, X, and Y, but now we see that each instance of Z has as duty soothing that is both a ProgrammingTask and TeachingAssistantShip; hence, it must be a subconcept of both X and Y, because it refines them both. So far, so good. The second axiom tells us that the intersection of ProgrammingTask and TeachingAssistantShip is empty, or: they are disjoint, or: there is no object that is both a teaching assistantship and a programming task. But each instance of Z has as duty to carry out a duty that is both a teaching assistantship and a programming task! This object cannot exist, hence, there cannot be a model where Z is instantiated, hence, Z is an unsatisfiable concept.
.png?revision=1&size=bestfit&width=932&height=367)
Figure 3.3.2: Graphical depiction of an approximation of \(\mathcal{KB}\) before checking concept subsumption \((\equiv\) not shown, nor are the subsumptions to Student, so as to avoid too much clutter).
Techniques: A Tableau for \(\mathcal{ALC}\)
The description of the deductions illustrated in the previous paragraph is an informal, high-level way of describing what the automated reasoner does when computing the concept hierarchy and checking for satisfiability. Clearly, such an informal way will not work as an algorithm to be implemented in a computer. There are
.png?revision=1&size=bestfit&width=1013&height=397)
Figure 3.3.3: Graphical depiction of \(\mathcal{K}\) after checking concept subsumption; content in green is deduced.
several proof techniques both in theory and in practice to realize the reasoning service. The most widely used technique at the time of writing (within the scope of DLs and the Semantic Web) is tableau reasoning, and is quite alike what we have seen with tableau with full FOL. In short, it:
- Unfold the TBox
- Convert the result into negation normal form (NNF)
- Apply the tableau rules to generate more ABoxes
- Stop when none of the rules are applicable
Then:
- \(\mathcal{T}\vdash C\sqsubseteq D\) if all ABoxes contain clashes
- \(\mathcal{T}\nvdash C\sqsubseteq D\) if some ABox does not contain a clash
First, recall that one enters the tableau in Negation Normal Form (NNF), i.e., “\(\neg\)” only in front of concepts. For DLs and \(C\) and \(D\) are concepts, \(R\) a role, we use equivalencies to obtain NNF, just like with FOL:
- \(\neg\neg C\) gives \(C\)
- \(\neg (C\sqcap D)\) gives \(\neg C\sqcup\neg D\)
- \(\neg (C\sqcup D)\) gives \(\neg C\sqcap\neg D\)
- \(\neg (\forall R.C)\) gives \(\exists R.\neg C\)
- \(\neg (\exists R.C)\) gives \(\forall R.\neg C\)
Second, there are the tableau rules. If there are more features, there will be more rules. These are the ones for \(\mathcal{ALC}\):
\(\sqcap\)-rule: If \((C_{1}\sqcap C_{2})(a)\in S\) but \(S\) does not contain both \(C_{1}(a)\) and \(C_{2}(a)\), then
\(S=S\cup\{ C_{1}(a), C_{2}(a)\}\)
\(\sqcup\)-rule: If \((C_{1}\sqcup C_{2})(a)\in S\) but \(S\) contains neither \(C_{1}(a)\) nor \(C_{2}(a)\), then
\(S=S\cup\{ C_{1}(a)\}\)
\(S=S\cup\{ C_{2}(a)\}\)
\(\forall\)-rule: If \((\forall R.C)(a)\in S\) and \(S\) contains \(R(a, b)\) but not \(C(b)\), then
\(S=S\cup\{C(b)\}\)
\(\exists\)-rule: If \((\exists R.C)(a)\in S\) and there is no \(b\) such that \(C(b)\) and \(R(a, b)\), then
\(S=S\cup\{C(b), R(a, b)\}\)
With these ingredients, it is possible to construct a tableau to prove that the aforementioned deductions hold. There will be an exercise about it, and we will see more aspects of automated reasoning in the lectures and exercises about OWL.


