1.4.4: Tarski’s world and formal structures
- Page ID
- 9865
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)To help you reason about sets of predicate logic statements, or even arguments expressed in predicate logic, we often use a ‘mathematical structure’. For some of these structures a visualisation in the form of Tarski’s world can sometimes be useful.
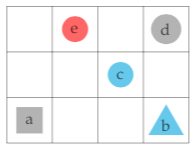
Figure 2.9: An instance of a Tarski World.
What is truth? In 1933, Polish mathematician Alfred Tarski (1901–1983) published a very long paper in Polish (titled Pojeçie prawdy w jez̧ykach nauk dedukcyjnych), setting out a mathematical definition of truth for formal languages. “Along with his contemporary, Kurt Gödel [who we’ll see in Chapter 4], he changed the face of logic in the twentieth century, especially through his work on the concept of truth and the theory of models.”

Source: en.Wikipedia.org/wiki/Alfred_Tarski.
In Tarski’s world, it is possible to describe situations using formulas whose truth can be evaluated, which are expressed in a first-order language that uses predicates such as Rightof(x, y), which means that x is situated—somewhere, not necessarily directly—to the right of y, or Blue(x), which means that x is blue. In the world in Figure 2.9, for instance, the formula ∀x(Triangle(x) → Blue(x)) holds, since all triangles are blue, but the converse of this formula, ∀x(Blue(x) → Triangle(x)), does not hold, since object c is blue but not a triangle.
Such an instance of Tarski world can be more formally described as a ‘mathematical structure’ (which we refer to as a formal structure occasionally). These structures allow us to evaluate statements in predicate logic as being true or false. To formalise a structure, we need to describe two things: the domain of discourse D of the structure and for all of the predicates, for which objects of the domain they are true. We do so using set-notationwhich we discuss in more depth in Chapter 4. The formal description of the structure S depicted in Figure 2.9 is:
• D = {a,b,c,d,e}
• Blue \(^{S}\) = {b, c}
• Gray \(^{S}\)= {a,d}
• Red \(^{S}\)= {e}
• Square \(^{S}\) = {a}
• Triangle \(^{S}\) = {b}
• Circle \(^{S}\) = {c,d,e}
• RightOf \(^{S}\) = {(b,a),(c,a),(d,a),(e,a), (b,c),(d,c),(b,e),(c,e),(d,e)}
• BelowOf \(^{S}\) ={(a,c),(a,d),(a,e),(b,c),(b, d), (b, e), (c, d), (c, e)}
• LeftOf \(^{S}\) = {(a,b),(c,b),(e,b),(a,c), (e, c), (a, d), (c, d), (e, d), (a, e)}
• AboveOf\(^{S}\) = {(c,a),(c,b),(d,a),(d,b), (d, c), (e, a), (e, b), (e, c)}
Notice that for the one-place predicates we have a set of objects for which this predicate is true (e.g., only b and c are blue) and such a set is denoted using ‘{’ and ‘}’ symbols, called‘curlybraces’orjust‘braces’.12 Forthetwo-place predicates we have a set of tuples that are denoted using ‘(’ and ‘)’ symbols, called ‘parentheses’ or ‘round brackets’. In this case, for instance, the fact that (a, b) is in the set LeftOf S means that LeftOf (a, b) is true for this structure, i.e., a is left of b.
Such formal structures can also be defined to disprove arguments written in predicate logic, as we will see in Section 2.5.3.

