3.5: Nondeterministic Finite-State Automata
- Page ID
- 6726
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As mentioned briefly above, there is an alternative school of thought as to what properties should be required of a finite-state automaton’s transition function. Recall our motivating example of a C++ compiler and a legal if statement. In our description, we had the compiler in an “expecting a ‘)’ ” state; on seeing a ‘)’, the compiler moved into an “expecting a ‘{’ or a legal statement” state. An alternative way to view this would be to say that the compiler, on seeing a ‘)’, could move into one of two different states: it could move to an “expecting a ‘{’” state or move to an “expecting a legal statement” state. Thus, from a single state, on input ‘)’, the compiler has multiple moves. This alternative interpretation is not allowed by the DFA model. A second point on which one might question the DFA model is the fact that input must be consumed for the machine to change state. Think of the syntax for C++ function declarations. The return type of a function need not be specified (the default is taken to be int). The start state of the compiler when parsing a function declaration might be “expecting a return type”; then with no input consumed, the compiler can move to the state “expecting a legal function name”. To model this, it might seem reasonable to allow transitions that do not require the consumption of input (such transitions are called ε-transitions). Again, this is not supported by the DFA abstraction. There is, therefore, a second class of finite-state automata that people study, the class of nondeterministic finite-state automata.
A nondeterministic finite-state automaton (NFA) is the same as a deterministic finite-state automaton except that the transition function is no longer a function that maps a state-input pair to a state; rather, it maps a state-input pair or a state-ε pair to a set of states. No longer do we have δ(q, a) = q′, meaning that the machine must change to state q′ if it is in state q and consumes an a. Rather, we have ∂(q,a) = {q1,q2,...,qn}, meaning that if the machine is in state q and consumes an a, it might move directly to any one of the states q1, . . . , qn. Note that the set of next states ∂(q,a) is defined for every state q and every input symbol a, but for someq’s and a’s it could be empty, or contain just one state (there don’t have to be multiple next states). The function ∂ must also specify whether it is possible for the machine to make any moves without input being consumed, i.e. ∂(q,ε) must be specified for every state q. Again, it is quite possible that ∂(q, ε) may be empty for some states q: there need not be ε-transitions out of q.
Definition 3.7
Formally, a nondeterministic finite-state automaton M is specified by 5 components: \(M=\left(Q, \Sigma, q_{0}, \partial, F\right)\) where
• Q, Σ, q0 and F are as in the definition of DFAs;
• ∂ is a transition function that takes <state, input symbol> pairs and maps each one to a set of states. To say \(\partial(q, a)=\left\{q_{1}, q_{2}, \dots, q_{n}\right\}\) means that if the machine is in state q and the input symbol a is consumed, then the machine may move directly into any one of states \(q_{1}, q_{2}, \dots, q_{n}\). The function ∂ must also be defined for every <state,ε>pair. To say \(\partial(q, \varepsilon)=\left\{q_{1}, q_{2}, \ldots, q_{n}\right\}\) means that there are direct ε- transitions from state q to each of \(q_{1}, q_{2}, \ldots, q_{n}\).
The formal description of the function \(\partial\) is \(\partial : Q \times(\Sigma \cup\{\varepsilon\}) \rightarrow \mathcal{P}(Q)\).
The function ∂ describes how the machine functions on zero or one input symbol. As with DFAs, we will often want to refer to the behavior of the machine on a string of inputs, and so we use the notation ∂∗(q,w) as shorthand for “the set of states in which the machine might be if it starts in state q and consumes input string w”. As with DFAs, ∂∗(q,w) is determined by the specification of ∂. Note that for every state q, ∂∗(q,ε) contains at least q, and may contain additional states if there are (sequences of) ε-transitions out of q.
We do have to think a bit carefully about what it means for an NFA to accept a string w. Suppose ∂∗(q0,w) contains both accepting and nonaccepting states, i.e. the machine could end in an accepting state after consuming w, but it might also end in a non-accepting state. Should we consider the machine to accept w, or should we require every state in \(\partial^{*}\left(q_{0}, w\right)\) to be accepting before we admit w to the ranks of the accepted? Think of the C++ compiler again: provided that an if statement fits one of the legal syntax specifications, the compiler will accept it. So we take as the definition of acceptance by an NFA: A string w is accepted by an NFA provided that at least one of the states in ∂∗(q0,w) is an accepting state. That is, if there is some sequence of steps of the machine that consumes wand leaves the machine in an accepting state, then the machine accepts w. Formally:
Definition 3.8
Let \(M=\left(Q, \Sigma, q_{0}, \partial, F\right)\) be a nondeterministic finite-state automaton. The string \(w \in \Sigma^{*}\) is accepted by \(M\) iff \(\partial^{*}\left(q_{0}, w\right)\) contains at least one state \(q_{F} \in F\).
The language accepted by M, denoted L(M), is the set of all strings \(w \in \Sigma^{*}\) that are accepted by \(M : L(M)=\left\{w \in \Sigma^{*} | \partial^{*}\left(q_{0}, w\right) \cap F \neq \emptyset\right\}\)
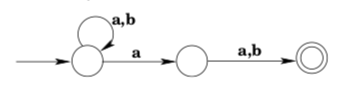
Example 3.16. The NFA shown below accepts all strings of a’s and b’s in which the second-to-last symbol is a.
It should be fairly clear that every language that is accepted by a DFA is also accepted by an NFA. Pictorially, a DFA looks exactly like an NFA (an NFA that doesn’t happen to have any ε-transitions or multiple same-label transitions from any state), though there is slightly more going on behind the scenes. Formally, given the DFA \(M=\left(Q, \Sigma, q_{0}, \delta, F\right)\), you can build an \(\mathrm{NFA} M^{\prime}=\left(Q, \Sigma, q_{0}, \partial, F\right)\) where 4 of the 5 components are the same and where every transition \(\delta(q, a)=q^{\prime}\) has been replaced by \(\partial(q, a)=\left\{q^{\prime}\right\}\).
But is the reverse true? Can any NFA recognized language be recognized by a DFA? Look, for example, at the language in Example 3.16. Can you come up with a DFA that accepts this language? Try it. It’s pretty difficult to do. But does that mean that there really is no DFA that accepts the language, or only that we haven’t been clever enough to find one?
It turns out that the limitation is in fact in our cleverness, and not in the power of DFAs.
Theorem 3.2. Every language that is accepted by an NFA is accepted by a DFA.
Proof. Suppose we are given an NFA \(N=\left(P, \Sigma, p_{0}, \partial, F_{p}\right)\), and we want to build a DFA \(D=\left(Q, \Sigma, q_{0}, \delta, F_{q}\right)\) that accepts the same language. The idea is to make the states in D correspond to subsets of N’s states, and then to set up D’s transition function δ so that for any string w, \(\delta^{*}\left(q_{0}, w\right)\) corresponds to \(\partial^{*}\left(p_{0}, w\right)\); i.e. the single state that w gets you to in D corresponds to the set of states that w could get you to in N. If any of those states is accepting in N, w would be accepted by N, and so the corresponding state in D would be made accepting as well.
So how do we make this work? The first thing to do is to deal with a start state q0 for D. If we’re going to make this state correspond to a subset of N’s states, what subset should it be? Well, remember (1) that in any DFA, \(\delta^{*}\left(q_{0}, \varepsilon\right)=q_{0} ;\) and \((2)\) we want to make \(\delta^{*}\left(q_{0}, w\right)\) correspond to∂∗(p0,w) for every w. Putting these two limitations together tells us that we should make q0 correspond to ∂∗(p0, ε). So q0 corresponds to the subset of all of N’s states that can be reached with no input.
Now we progressively set up D’s transition function δ by repeatedly doing the following:
– find a state q that has been added to D but whose out-transitions have not yet been added. (Note that q0 initially fits this description.) Remember that the state q corresponds to some subset \(\left\{p_{1}, \ldots, p_{n}\right\}\) of \(N^{\prime}\) s states.
– for each input symbol a, look at all N’s states that can be reached from any one of \(p_{1}, \ldots, p_{n}\) by consuming a (perhaps making some ε-transitions as well). That is, look at \(\partial^{*}\left(p_{1}, a\right) \cup \ldots \cup \partial^{*}\left(p_{n}, a\right)\). If there is not already a DFA state q′ that corresponds to this subset of N’s states, then add one, and add the transition δ(q, a) = q′ to D’s transitions.
The above process must halt eventually, as there are only a finite number of states n in the NFA, and therefore there can be at most \(2^{n}\) states in the DFA, as that is the number of subsets of the NFA’s states. The final states of the new DFA are those where at least one of the associated NFA states is an accepting state of the NFA.
Can we now argue that L(D) = L(N)? We can, if we can argue that \(\delta^{*}\left(q_{0}, w\right)\) corresponds to \(\partial^{*}\left(p_{0}, w\right)\) for all \(w \in \Sigma^{*}\): if this latter property holds, then \(w \in L(D)\) iff \(\delta^{*}\left(q_{0}, w\right)\) is accepting, which we made be so iff \(\partial^{*}\left(p_{0}, w\right)\) contains an accepting state of N, which happens iff N accepts w i.e. iff \(w \in L(N)\)
So can we argue that \(\delta^{*}\left(q_{0}, w\right)\) does in fact correspond to \(\partial^{*}\left(p_{0}, w\right)\) for all w? We can, using induction on the length of w.
First, a preliminary observation. Suppose w = xa, i.e. w is the string x followed by the single symbol a. How are \(\partial^{*}\left(p_{0}, x\right)\) and \(\partial^{*}\left(p_{0}, w\right)\) related?
Well, recall that \(\partial^{*}\left(p_{0}, x\right)\) is the set of all states that \(N\) can reach when it starts in \(p_{0}\) and consumes \(x : \partial^{*}\left(p_{0}, x\right)=\left\{p_{1}, \ldots, p_{n}\right\}\) for some states \(p_{1}, \dots, p_{n}\) Now, w is just x with an additional a, so where might N end up if it starts in\(p_{0}\) and consumes \(w\)? We know that \(x\) gets \(N\) to \(p_{1}\) or...or \(p_{n}\), so xa gets N to any state that can be reached from p1 with an a(and maybe some ε-transitions), and to any state that can be reached from p2 with an a (and maybe some ε-transitions), etc. Thus, our relationship between \(\partial^{*}\left(p_{0}, x\right)\) and \(\partial^{*}\left(p_{0}, w\right)\) is that if \(\partial^{*}\left(p_{0}, x\right)=\left\{p_{1}, \ldots, p_{n}\right\}\), then \(\partial^{*}\left(p_{0}, w\right)=\partial^{*}\left(p_{1}, a\right) \cup \ldots \cup \partial^{*}\left(p_{n}, a\right)\) With this observation in hand, let’s proceed to our proof by induction.
We want to prove that \(\delta^{*}\left(q_{0}, w\right)\) corresponds to \(\partial^{*}\left(p_{0}, w\right)\) for all \(w \in \Sigma^{*}\). We use induction on the length of w.
- Base case: Suppose w has length 0. The only string w with length 0 is ε, so we want to show that δ∗(q0,ε) corresponds to ∂∗(p0,ε). Well, δ∗(q0, ε) = q0, since in a DFA, δ∗(q, ε) = q for any state q. We explicitly made q0 correspond to ∂∗(p0,ε), and so the property holds for w with length 0.
- Inductive case: Assume that the desired property holds for some number n, i.e. that δ∗(q0,x) corresponds to ∂∗(p0,x) for all x with length n. Look at an arbitrary string w with length n + 1. We want to show that δ∗(q0, w) corresponds to ∂∗(p0, w). Well, the string w must look like xa for some string x (whose length is n) and some symbol a. By our inductive hypothesis, we know δ∗(q0, x) corresponds to ∂∗(p0, x). We know ∂∗(p0,x) is a set of N’s states, say ∂∗(p0,x) = {p1,...,pn}. We know ∂∗(p0,x) is a set of N’s states, say ∂∗(p0,x) = {p1,...,pn}. At this point, our subsequent reasoning might be a bit clearer if we give explicit names to δ∗(q0,w) (the state D reaches on input w) andδ∗(q0,x) (the state D reaches on input x). Call δ∗(q0,w) qw, and call δ∗(q0,x) qx. We know, because w = xa, there must be an a- transition from qx to qw. Look at how we added transitions to δ: the fact that there is an a-transition from \(q_{x}\) to \(q_{w}\) means that \(q_{w}\) corresponds to the set \(\partial^{*}\left(p_{1}, a\right) \cup \ldots \cup \partial^{*}\left(p_{n}, a\right)\) of \(N^{\prime}\) 's states. By our preliminary observation, \(\partial^{*}\left(p_{1}, a\right) \cup \ldots \cup \partial^{*}\left(p_{n}, a\right)\) is just \(\partial^{*}\left(p_{0}, w\right)\). So \(q_{w}\left(\text { or } \delta^{*}\left(q_{0}, w\right)\right)\) corresponds to \(\partial^{*}\left(p_{0}, w\right)\), which is what we wanted to prove. Since w was an arbitrary string of length n + 1, we have shown that the property holds for n + 1.
Altogether, we have shown by induction that \(\delta^{*}\left(q_{0}, w\right)\) corresponds to \(\partial^{*}\left(p_{0}, w\right)\) for all \(w \in \Sigma^{*}\). As indicated at the very beginning of this proof, that is enough to prove that L(D) = L(N). So for any NFA N, we can find a DFA D that accepts the same language.
Example 3.17
Consider the NFA shown below.
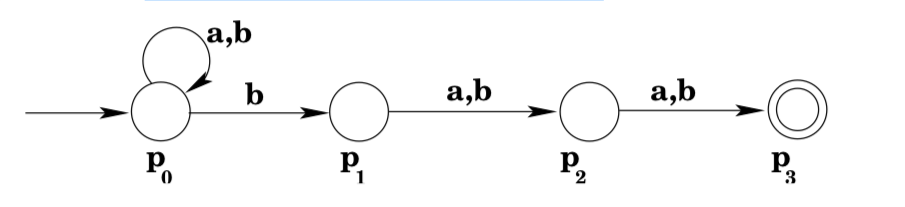
We start by looking at \(\partial^{*}\left(p_{0}, \varepsilon\right)\), and then add transitions and states as described above.
- \(\partial^{*}\left(p_{0}, \varepsilon\right)=\left\{p_{0}\right\}\) so \(q_{0}=\left\{p_{0}\right\}\)
- \(\delta\left(q_{0}, a\right)\) will be \(\partial^{*}\left(p_{0}, a\right),\) which is \(\left\{p_{0}\right\},\) so \(\delta\left(q_{0}, a\right)=q_{0}\)
- \(\delta\left(q_{0}, b\right)\) will be \(\partial^{*}\left(p_{0}, b\right),\) which is \(\left\{p_{0}, p_{1}\right\},\) so we need to add a new
state \(q_{1}=\left\{p_{0}, p_{1}\right\}\) to the \(\mathrm{DFA} ;\) and add \(\delta\left(q_{0}, b\right)=q_{1}\) to the DFA's
transition function. - \(\delta\left(q_{1}, a\right)\) will be \(\partial^{*}\left(p_{0}, a\right)\) unioned with \(\partial^{*}\left(p_{1}, a\right)\) since \(q_{1}=\left\{p_{0}, p_{1}\right\}\)
since \(\partial^{*}\left(p_{0}, a\right) \cup \partial^{*}\left(p_{1}, a\right)=\left\{p_{0}\right\} \cup\left\{p_{2}\right\}=\left\{p_{0}, p_{2}\right\},\) we need to add a new state \(q_{2}=\left\{p_{0}, p_{2}\right\}\) to the DFA, and a transition \(\delta\left(q_{1}, a\right)=q_{2}\) - \(\delta\left(q_{1}, b\right)\) will be \(\partial^{*}\left(p_{0}, b\right)\) unioned with \(\partial^{*}\left(p_{1}, b\right),\) which gives \(\left\{p_{0}, p_{1}\right\} \cup\)\(\left\{p_{2}\right\},\) which again gives us a new state \(q_{3}\) to add to the DFA, together with the transition \(\delta\left(q_{1}, b\right)=q_{3}\)
At this point, our partially-constructed DFA looks as shown below:
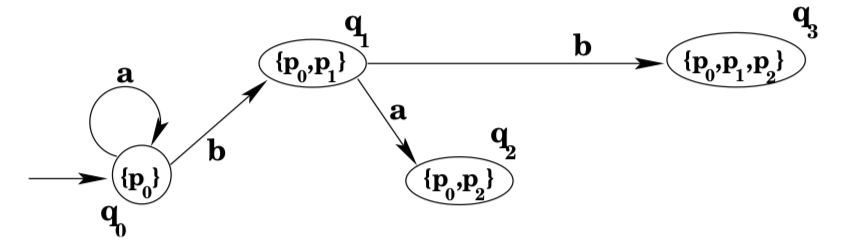
The construction continues as long as there are new states being added, and new transitions from those states that have to be computed. The final DFA is shown below.
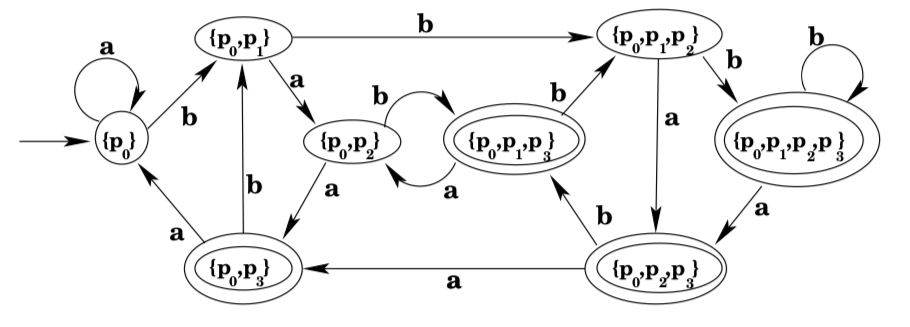
Exercises
- What language does the NFA in Example 3.17 accept?
- Give a DFA that accepts the language accepted by the following NFA.
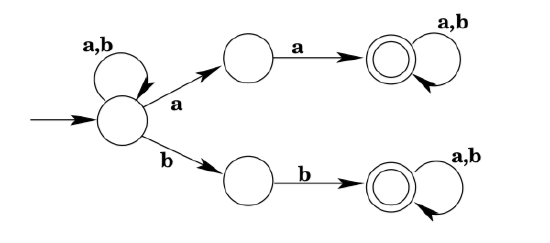
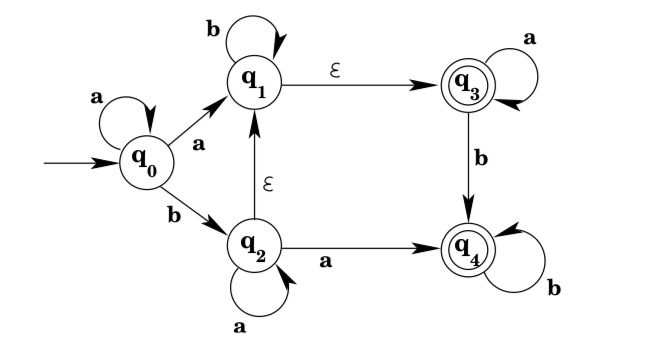
3. Give a DFA that accepts the language accepted by the following NFA. (Be sure to note that, for example, it is possible to reach both q1 and q3 from q0on consumption of an a, because of the ε-transition.)