1.2: Signals Represent Information
- Page ID
- 1593
- A brief discussion of information and signals.
- Introduction to the notion of continuous and discrete-time signals.
Whether analog or digital, information is represented by the fundamental quantity in electrical engineering: the signal. Stated in mathematical terms, a signal is merely a function. Analog signals are continuous-valued; digital signals are discrete-valued. The independent variable of the signal could be time (speech, for example), space (images), or the integers (denoting the sequencing of letters and numbers in the football score).
Analog Signals
Analog signals are usually signals defined over continuous independent variable(s). Speech is produced by your vocal cords exciting acoustic resonances in your vocal tract. The result is pressure waves propagating in the air, and the speech signal thus corresponds to a function having independent variables of space and time and a value corresponding to air pressure:\[s(x,t) \nonumber \]
Here we use vector notation \[x \nonumber \]
to denote spatial coordinates.
When you record someone talking, you are evaluating the speech signal at a particular spatial location, \[x_{0} \nonumber \]
say.
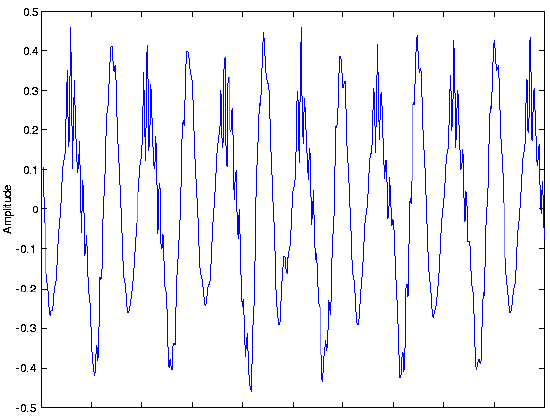
An example of the resulting waveform \[s(x_{0},t) \nonumber \]
is shown in the Figure 1.2.1:
Photographs are static, and are continuous-valued signals defined over space. Black-and-white images have only one value at each point in space, which amounts to its optical reflection properties. In the Figure 1.2.2 an image is shown, demonstrating that it (and all other images as well) are functions of two independent spatial variables.

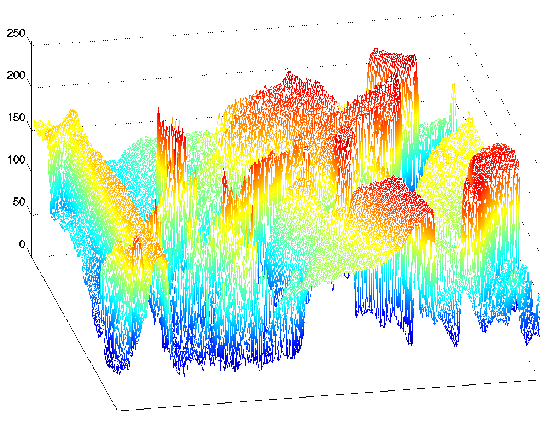
(a) (b)
Figure 1.2.2 On the left is the classic Lena image, which is used ubiquitously as a test image. It contains straight and curved lines, complicated texture, and a face. On the right is a perspective display of the Lena image as a signal: a function of two spatial variables. The colors merely help show what signal values are about the same size. In this image, signal values range between 0 and 255; why is that?
Color images have values that express how reflectivity depends on the optical spectrum. Painters long ago found that mixing together combinations of the so-called primary colors--red, yellow and blue--can produce very realistic color images. Thus, images today are usually thought of as having three values at every point in space, but a different set of colors is used: How much of red, green and blue is present. Mathematically, color pictures are multivalued--vector-valued--signals:
\[s(x)=\left ( r(x),g(x),b(x) \right )^{T} \nonumber \]
Interesting cases abound where the analog signal depends not on a continuous variable, such as time, but on a discrete variable. For example, temperature readings taken every hour have continuous--analog--values, but the signal's independent variable is (essentially) the integers.
Digital Signals
The word "digital" means discrete-valued and implies the signal has an integer-valued independent variable. Digital information includes numbers and symbols (characters typed on the keyboard, for example). Computers rely on the digital representation of information to manipulate and transform information. Symbols do not have a numeric value, and each is represented by a unique number. The ASCII character code has the upper- and lowercase characters, the numbers, punctuation marks, and various other symbols represented by a seven-bit integer. For example, the ASCII code represents the letter
The word "digital" means discrete-valued and implies the signal has an integer-valued independent variable. Digital information includes numbers and symbols (characters typed on the keyboard, for example). Computers rely on the digital representation of information to manipulate and transform information. Symbols do not have a numeric value, and each is represented by a unique number. The ASCII character code has the upper- and lowercase characters, the numbers, punctuation marks, and various other symbols represented by a seven-bit integer. For example, the ASCII code represents the letter a as the number 97 and the letter A as 65. Table 1.2.1 shows the international convention on associating characters with integers.
| 00 | nul | 01 | soh | 02 | stx | 03 | etx | 04 | eot | 05 | enq | 06 | ack | 07 | bel |
| 08 | bs | 09 | ht | 0A | nl | 0B | vt | 0C | np | 0D | cr | 0E | so | 0F | si |
| 10 | dle | 11 | dc1 | 12 | dc2 | 13 | dc3 | 14 | dc4 | 15 | nak | 16 | syn | 17 | etb |
| 18 | car | 19 | em | 1A | sub | 1B | esc | 1C | fs | 1D | gs | 1E | rs | 1F | us |
| 20 | sp | 21 | ! | 22 | " | 23 | # | 24 | $ | 25 | % | 26 | & | 27 | ' |
| 28 | ( | 29 | ) | 2A | * | 2B | + | 2C | , | 2D | - | 2E | . | 2F | / |
| 30 | 0 | 31 | 1 | 32 | 2 | 33 | 3 | 34 | 4 | 35 | 5 | 36 | 6 | 37 | 7 |
| 38 | 8 | 39 | 9 | 3A | : | 3B | ; | 3C | < | 3D | = | 3E | > | 3F | ? |
| 40 | @ | 41 | A | 42 | B | 43 | C | 44 | D | 45 | E | 46 | F | 47 | G |
| 48 | H | 49 | I | 4A | J | 4B | K | 4C | L | 4D | M | 4E | N | 4F | 0 |
| 50 | P | 51 | Q | 52 | R | 53 | S | 54 | T | 55 | U | 56 | V | 57 | W |
| 58 | X | 59 | Y | 5A | Z | 5B | [ | 5C | \ | 5D | ] | 5E | ^ | 5F | _ |
| 60 | ' | 61 | a | 62 | b | 63 | c | 64 | d | 65 | e | 66 | f | 67 | g |
| 68 | h | 69 | i | 6A | j | 6B | k | 6C | l | 6D | m | 6E | n | 6F | o |
| 70 | p | 71 | q | 72 | r | 73 | s | 74 | t | 75 | u | 76 | v | 77 | w |
| 78 | x | 79 | y | 7A | z | 7B | { | 7C | | | 7D | } | 7E | ~ | 7F | del |


