5.9: Fast Fourier Transform (FFT)
- Page ID
- 1827
- The DFT can be reduced from exponential time with the Fast Fourier Transform algorithm.
One wonders if the DFT can be computed faster: Does another computational procedure -- an algorithm -- exist that can compute the same quantity, but more efficiently. We could seek methods that reduce the constant of proportionality, but do not change the DFT's complexity O(N2). Here, we have something more dramatic in mind: Can the computations be restructured so that a smaller complexity results?
In 1965, IBM researcher Jim Cooley and Princeton faculty member John Tukey developed what is now known as the Fast Fourier Transform (FFT). It is an algorithm for computing that DFT that has order O(N log N) for certain length inputs. Now when the length of data doubles, the spectral computational time will not quadruple as with the DFT algorithm; instead, it approximately doubles. Later research showed that no algorithm for computing the DFT could have a smaller complexity than the FFT. Surprisingly, historical work has shown that Gauss in the early nineteenth century developed the same algorithm, but did not publish it! After the FFT's rediscovery, not only was the computation of a signal's spectrum greatly speeded, but also the added feature of algorithm meant that computations had flexibility not available to analog implementations.
Before developing the FFT, let's try to appreciate the algorithm's impact. Suppose a short-length transform takes 1 ms. We want to calculate a transform of a signal that is 10 times longer. Compare how much longer a straightforward implementation of the DFT would take in comparison to an FFT, both of which compute exactly the same quantity.
Solution
If a DFT required 1ms to compute, and signal having ten times the duration would require 100ms to compute. Using the FFT, a 1ms computing time would increase by a factor of about
\[10\log_{2}10=33 \nonumber \]
A factor of 3 less than the DFT would have needed.
To derive the FFT, we assume that the signal's duration is a power of two:
\[N=2^{L} \nonumber \]
Consider what happens to the even-numbered and odd-numbered elements of the sequence in the DFT calculation.
\[S(k)=s(0)+s(2)e^{(-i)\frac{2\pi 2k}{N}}+...+s(N-2)e^{(-i)\frac{2\pi (N-2)k}{N}}+s(1)e^{(-i)\frac{2\pi k}{N}}+s(3)e^{(-i)\frac{2\pi \times (2+1)k}{N}}+...+s(N-1)e^{(-i)\frac{2\pi (N-(2-1))k}{N}} \nonumber \]
\[S(k)=\left [ s(0)+s(2)e^{(-i)\frac{2\pi 2k}{\frac{N}{2}}}+...+s(N-2)e^{(-i)\frac{2\pi \left ( \frac{N}{2}-1 \right )k}{\frac{N}{2}}}\right ]+\left [ s(1)e^{(-i)\frac{2\pi k}{N}}+s(3)e^{(-i)\frac{2\pi k}{\frac{N}{2}}}+...+s(N-1)e^{(-i)\frac{2\pi \left ( \frac{N}{2}-1 \right )k}{\frac{N}{2}}}\right ]e^{\frac{-(i2\pi k)}{N}} \nonumber \]
Each term in square brackets has the form of a N/2 length DFT. The first one is a DFT of the even-numbered elements, and the second of the odd-numbered elements. The first DFT is combined with the second multiplied by the complex exponential \[e^{\frac{-(i2\pi k)}{N}} \nonumber \]
The half-length transforms are each evaluated at frequency indices k=0,...,N-1. Normally, the number of frequency indices in a DFT calculation range between zero and the transform length minus one. The computational advantage of the FFT comes from recognizing the periodic nature of the discrete Fourier transform. The FFT simply reuses the computations made in the half-length transforms and combines them through additions and the multiplication by \[e^{\frac{-(i2\pi k)}{N}} \nonumber \] which is not periodic over N/2.
Figure 5.9.1 below illustrates this decomposition. As it stands, we now compute two length N/2 transforms of complexity
\[2O\left ( \frac{N^{2}}{4} \right ) \nonumber \]
multiply one of them by the complex exponential of complexity O(N) and add the results (complexity O(N)). At this point, the total complexity is still dominated by the half-length DFT calculations, but the proportionality coefficient has been reduced.
Now for the fun. Because
\[N=2^{L} \nonumber \]
each of the half-length transforms can be reduced to two quarter-length transforms, each of these to two eighth-length ones, etc. This decomposition continues until we are left with length-2 transforms. This transform is quite simple, involving only additions. Thus, the first stage of the FFT has N/2 length-2 transforms (see the bottom part of Figure 5.9.1). Pairs of these transforms are combined by adding one to the other multiplied by a complex exponential. Each pair requires 4 additions and 2 multiplications, giving a total number of computations equaling
\[6\cdot \frac{N}{4}=\frac{3N}{2} \nonumber \]
This number of computations does not change from stage to stage. Because the number of stages, the number of times the length can be divided by two, equals \[\log_{2}N \nonumber \] the number of arithmetic operations equals
\[\frac{3N}{2}\log_{2}N \nonumber \]
which makes the complexity of the FFT
\[O(N\log_{2}N) \nonumber \]
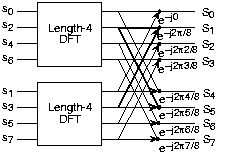
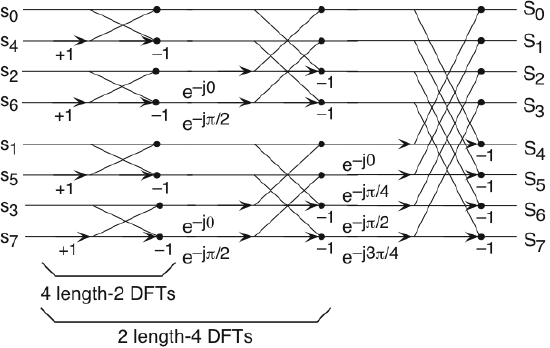
Figure 5.9.1 the initial decomposition of a length-8 DFT into the terms using even- and odd-indexed inputs marks the first phase of developing the FFT algorithm. When these half-length transforms are successively decomposed, we are left with the diagram shown in the bottom panel that depicts the length-8 FFT computation.
Doing an example will make computational savings more obvious. Let's look at the details of a length-8 DFT. As shown on Figure 5.9.1b, Doing an example will make computational savings more obvious. Let's look at the details of a length-8 DFT. Considering Figure 5.9.2 below, as the frequency index goes from 0 through 7, we recycle values from the length-4 DFTs into the final calculation because of the periodicity of the DFT output. Examining how pairs of outputs are collected together, we create the basic computational element known as a butterfly as shown in Figure 5.9.2.
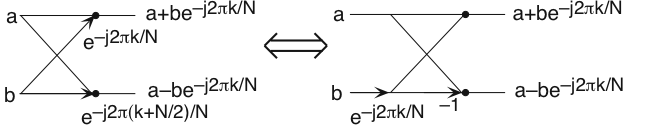
By considering together the computations involving common output frequencies from the two half-length DFTs, we see that the two complex multiplies are related to each other, and we can reduce our computational work even further. By further decomposing the length-4 DFTs into two length-2 DFTs and combining their outputs, we arrive at the diagram summarizing the length-8 fast Fourier transform (Figure 5.9.1b). Although most of the complex multiplies are quite simple such as multiplying by
\[e^{-(i\frac{\pi }{2})} \nonumber \]
means swapping real and imaginary parts and changing their signs. Let's count those for purposes of evaluating the complexity as full complex multiplies.
We have N/2 = 4 complex multiplies and N = 8 complex additions for each stage and
\[\log_{2}N=3 \nonumber \]
stages, making the number of basic computations
\[\frac{3N}{2}\log_{2}N \nonumber \]
as predicted.
Note that the ordering of the input sequence in the two parts of Figure 5.9.1 aren't quite the same. Why not? How is the ordering determined?
Solution
The upper panel has not used the FFT algorithm to compute the length-4 DFTs while the lower one has. The ordering is determined by the algorithm.
Other "fast" algorithms were discovered, all of which make use of how many common factors the transform length
Suppose the length of the signal were 500? How would you compute the spectrum of this signal using the Cooley-Tukey algorithm? What would the length N of the transform be?
Solution
The transform can have any greater than or equal to the actual duration of the signal. We simply “pad” the signal with zero-valued samples until a computationally advantageous signal length results. Recall that the FFT is an algorithm to compute the DFT. Extending the length of the signal this way merely means we are sampling the frequency axis more finely than required. To use the Cooley-Tukey algorithm, the length of the resulting zero-padded signal can be 512, 1024, etc. samples long.


