3.12: Voltage Reflection Coefficient
- Page ID
- 6278
We now consider the scenario shown in Figure \(\PageIndex{1}\). Here a wave arriving from the left along a lossless transmission line having characteristic impedance \(Z_0\) arrives at a termination located at \(z=0\). The impedance looking into the termination is \(Z_L\), which may be real-, imaginary-, or complex-valued. The questions are: Under what circumstances is a reflection – i.e., a leftward traveling wave – expected, and what precisely is that wave?
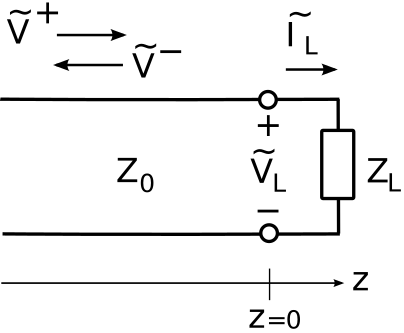
The potential and current of the incident wave are related by the constant value of \(Z_0\). Similarly, the potential and current of the reflected wave are related by \(Z_0\). Therefore, it suffices to consider either potential or current. Choosing potential, we may express the incident wave as \[\widetilde{V}^+(z) = V_0^+ e^{-j\beta z} \nonumber \] where \(V_0^+\) is determined by the source of the wave, and so is effectively a “given.” Any reflected wave must have the form \[\widetilde{V}^-(z) = V_0^- e^{+j\beta z} \nonumber \] Therefore, the problem is solved by determining the value of \(V_0^-\) given \(V_0^+\), \(Z_0\), and \(Z_L\).
Considering the situation at \(z=0\), note that by definition we have \[Z_L \triangleq \frac{\widetilde{V}_L}{\widetilde{I}_L} \label{m0084_eZL} \] where \(\widetilde{V}_L\) and \(\widetilde{I}_L\) are the potential across and current through the termination, respectively. Also, the potential and current on either side of the \(z=0\) interface must be equal. Thus,
\begin{align}
\widetilde{V}^{+}(0)+\widetilde{V}^{-}(0) &=\widetilde{V}_{L} \label{m0084_eV1} \\
\widetilde{I}^{+}(0)+\widetilde{I}^{-}(0) &=\widetilde{I}_{L} \label{m0084_eI1}
\end{align}
where \(\widetilde{I}^+(z)\) and \(\widetilde{I}^-(z)\) are the currents associated with \(\widetilde{V}^+(z)\) and \(\widetilde{V}^-(z)\), respectively. Since the voltage and current are related by \(Z_0\), Equation \ref{m0084_eI1} may be rewritten as follows:
\[\frac{\widetilde{V}^+(0)}{Z_0} - \frac{\widetilde{V}^-(0)}{Z_0} = \widetilde{I}_L \label{m0084_eI2} \]
Evaluating the left sides of Equations \ref{m0084_eV1} and \ref{m0084_eI2} at \(z=0\), we find:
\begin{aligned}
V_{0}^{+}+V_{0}^{-} &=\widetilde{V}_{L} \\
\frac{V_{0}^{+}}{Z_{0}}-\frac{V_{0}^{-}}{Z_{0}} &=\widetilde{I}_{L}
\end{aligned}
Substituting these expressions into Equation \ref{m0084_eZL} we obtain: \[Z_L = \frac{V_0^+ + V_0^-}{V_0^+/Z_0 - V_0^-/Z_0} \nonumber \] Solving for \(V_0^-\) we obtain \[V_0^- = \frac{Z_L-Z_0}{Z_L+Z_0}~V_0^+ \nonumber \]
Thus, the answer to the question posed earlier is that \[V_0^- = \Gamma V_0^+ ~~\mbox{, where} \nonumber \] \[\boxed{ \Gamma \triangleq \frac{Z_L-Z_0}{Z_L+Z_0} } \label{m0084_eGamma} \]
The quantity \(\Gamma\) is known as the voltage reflection coefficient. Note that when \(Z_L=Z_0\), \(\Gamma=0\) and therefore \(V_0^-=0\). In other words,
If the terminating impedance is equal to the characteristic impedance of the transmission line, then there is no reflection.
If, on the other hand, \(Z_L \neq Z_0\), then \(\left|\Gamma\right|>0\), \(V_0^-= \Gamma V_0^+\), and a leftward-traveling reflected wave exists.
Since \(Z_L\) may be real-, imaginary-, or complex-valued, \(\Gamma\) too may be real-, imaginary-, or complex-valued. Therefore, \(V_0^-\) may be different from \(V_0^+\) in magnitude, sign, or phase.
Note also that \(\Gamma\) is not the ratio of \(I_0^-\) to \(I_0^+\). The ratio of the current coefficients is actually \(-\Gamma\). It is quite simple to show this with a simple modification to the above procedure and is left as an exercise for the student.
Summarizing:
The voltage reflection coefficient \(\Gamma\), given by Equation \ref{m0084_eGamma}, determines the magnitude and phase of the reflected wave given the incident wave, the characteristic impedance of the transmission line, and the terminating impedance.
We now consider values \(\Gamma\) that arise for commonly-encountered terminations.
Matched Load. (\(Z_L = Z_0\)). In this case, the termination may be a device with impedance \(Z_0\), or the termination may be another transmission line having the same characteristic impedance. When \(Z_L = Z_0\), \(\Gamma = 0\) and there is no reflection.
Open Circuit. An “open circuit” is the absence of a termination. This condition implies \(Z_{L} \rightarrow \infty\), and subsequently \(\Gamma \rightarrow+1\). Since the current reflection coefficient is \(-\Gamma\), the reflected current wave is 180◦ out of phase with the incident current wave, making the total current at the open circuit equal to zero, as expected.
Short Circuit. “Short circuit” means \(Z_L = 0\), and subsequently \(\Gamma = −1\). In this case, the phase of \(\Gamma\) is 180◦, and therefore, the potential of the reflected wave cancels the potential of the incident wave at the open circuit, making the total potential equal to zero, as it must be. Since the current reflection coefficient is \(−\Gamma = +1\) in this case, the reflected current wave is in phase with the incident current wave, and the magnitude of the total current at the short circuit non-zero as expected.
Purely Reactive Load. A purely reactive load, including that presented by a capacitor or inductor, has \(Z_L = jX\) where \(X\) is reactance. In particular, an inductor is represented by \(X > 0\) and a capacitor is represented by \(X < 0\). We find
\[\Gamma=\frac{-Z_{0}+j X}{+Z_{0}+j X} \nonumber \]
The numerator and denominator have the same magnitude, so \(|\Gamma| = 1\). Let \(\phi\) be the phase of the denominator (\(+Z_0 + jX\)). Then, the phase of the numerator is \(\pi − \phi\). Subsequently, the phase of \(\Gamma\) is \((\pi-\phi)-\phi=\pi-2 \phi\). Thus, we see that the phase of \(\Gamma\) is no longer limited to be 0◦ or 180◦ , but can be any value in between. The phase of reflected wave is subsequently shifted by this amount.
Other Terminations. Any other termination, including series and parallel combinations of any number of devices, can be expressed as a value of \(Z_L\) which is, in general, complex-valued. The associated value of \(|\Gamma|\) is limited to the range 0 to 1. To see this, note:
\[\Gamma=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}=\frac{Z_{L} / Z_{0}-1}{Z_{L} / Z_{0}+1} \nonumber \]
Note that the smallest possible value of \(|\Gamma|\) occurs when the numerator is zero; i.e., when \(Z_L = Z_0\). Therefore, the smallest value of \(|\Gamma|\) is zero. The largest possible value of \(|\Gamma|\) occurs when \(Z_{L} / Z_{0} \rightarrow \infty\) (i.e., an open circuit) or when \(Z_L/Z_0 = 0\) (a short circuit); the result in either case is \(|\Gamma| = 1\). Thus,
\[ \boxed{ 0 \leq|\Gamma| \leq 1 } \nonumber \]


