3.11: Microstrip Line
- Page ID
- 6277
A microstrip transmission line consists of a narrow metallic trace separated from a metallic ground plane by a slab of dielectric material, as shown in Figure \(\PageIndex{1}\). This is a natural way to implement a transmission line on a printed circuit board, and so accounts for an important and expansive range of applications. The reader should be aware that microstrip is distinct from stripline, which is a very different type of transmission line; see “Additional Reading” at the end of this section for disambiguation of these terms.
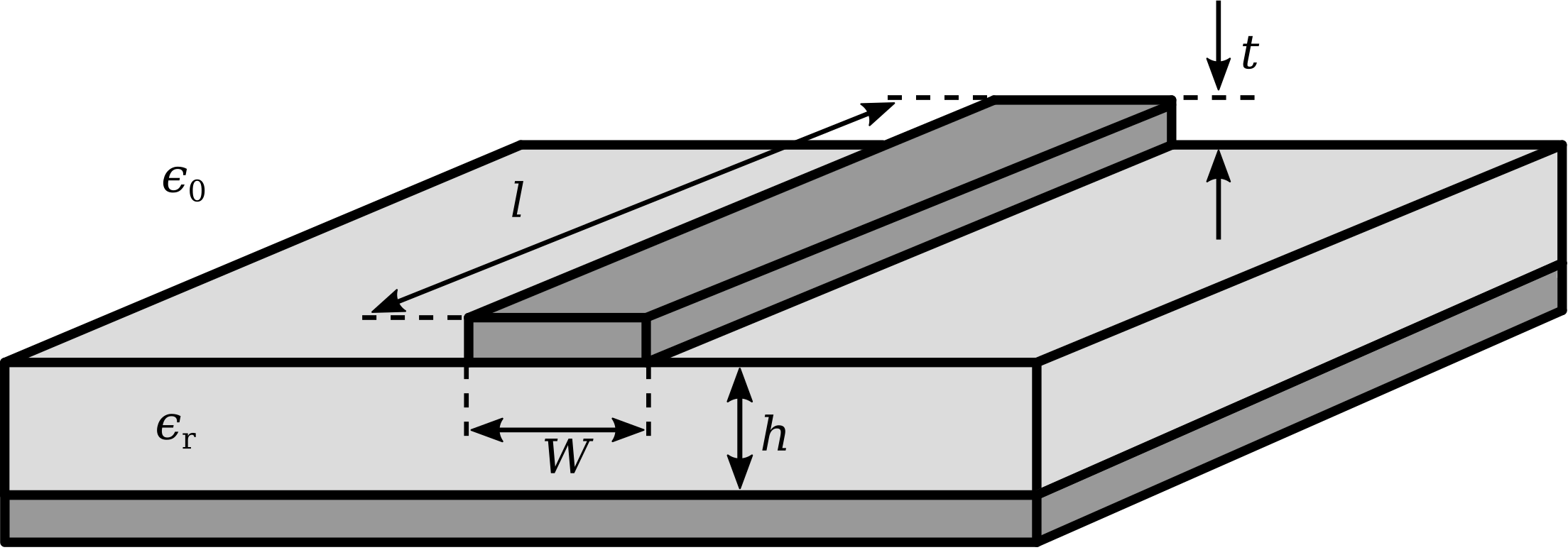
A microstrip line is single-ended1 in the sense that the conductor geometry is asymmetric and the one conductor – namely, the ground plane – also normally serves as ground for the source and load.
The spacer material is typically a low-loss dielectric material having permeability approximately equal to that of free space (\(\mu \approx \mu_0\)) and relative permittivity \(\epsilon_r\) in the range 2 to about 10 or so.
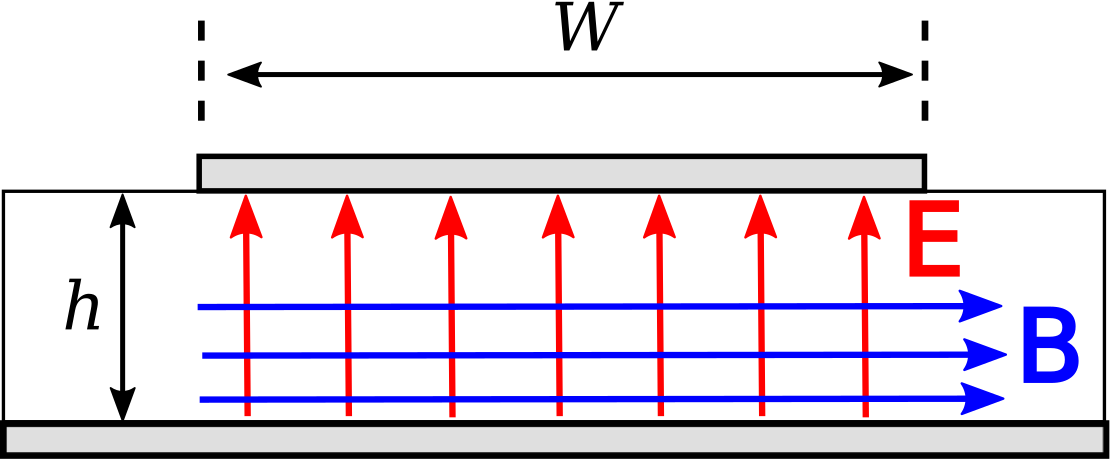
A microstrip line nominally exhibits TEM field structure. This structure is shown in Figure \(\PageIndex{2}\). Note that electric and magnetic fields exist both in the dielectric and in the space above the dielectric, which is typically (but not always) air. This complex field structure makes it difficult to describe microstrip line concisely in terms of the equivalent circuit parameters of the lumped-element model. Instead, expressions for \(Z_0\) directly in terms of \(h/W\) and \(\epsilon_r\) are typically used instead. A variety of these expressions are in common use, representing different approximations and simplifications. A widely-accepted and broadly-applicable expression is:2
\[Z_0 \approx \frac{42.4~\Omega}{\sqrt{\epsilon_r+1}} ~\times \ln\left[ 1 + \frac{4h}{W'} \left( \Phi + \sqrt{ \Phi^2 + \frac{1+1/\epsilon_r}{2}\pi^2 } \right) \right] \label{m0082_eWheeler10} \]
where \[\Phi \triangleq \frac{ 14 + 8/\epsilon_r }{ 11 } \left( \frac{4h}{W'} \right) \nonumber \]
and \(W'\) is \(W\) adjusted to account for the thickness \(t\) of the microstrip line. Typically \(t\ll W\) and \(t \ll h\), for which \(W'\approx W\). Simpler approximations for \(Z_0\) are also commonly employed in the design and analysis of microstrip lines. These expressions are limited in the range of \(h/W\) for which they are valid, and can usually be shown to be special cases or approximations of Equation \ref{m0082_eWheeler10}. Nevertheless, they are sometimes useful for quick “back of the envelope” calculations.
Accurate expressions for wavelength \(\lambda\), phase propagation constant \(\beta\), and phase velocity \(v_p\) are similarly difficult to obtain for waves in microstrip line. An approximate technique employs a result from the theory of uniform plane waves in unbounded media (Equation 9.2.18 from Section 9.2):
\[\beta = \omega\sqrt{\mu\epsilon} \nonumber \]
It turns out that the electromagnetic field structure in the space between the conductors is well-approximated as that of a uniform plane wave in unbounded media having the same permeability \(\mu_0\) but a different relative permittivity, which we shall assign the symbol \(\epsilon_{r,eff}\) (for “effective relative permittivity”). Then
\begin{aligned}
\beta & \approx \omega \sqrt{\mu_{0} \epsilon_{r, e f f} \epsilon_{0}} \: (\text { low-loss microstrip }) \\
&=\beta_{0} \sqrt{\epsilon_{r, e f f}}
\end{aligned}
In other words, the phase propagation constant in a microstrip line can be approximated as the free-space phase propagation \(\beta_0\triangleq\omega\sqrt{\mu_0\epsilon_0}\) times a correction factor \(\sqrt{\epsilon_{r,eff}}\). Then \(\epsilon_{r,eff}\) may be crudely approximated as follows:
\[\epsilon_{r,eff} \approx \frac{\epsilon_r+1}{2} \nonumber \]
i.e., \(\epsilon_{r,eff}\) is roughly the average of the relative permittivity of the dielectric slab and the relative permittivity of free space. The assumption employed here is that \(\epsilon_{r,eff}\) is approximately the average of these values because some fraction of the power in the guided wave is in the dielectric, and the rest is above the dielectric. Various approximations are available to improve on this approximation; however, in practice variations in the value of \(\epsilon_r\) for the dielectric due to manufacturing processes typically make a more precise estimate irrelevant.
Using this concept, we obtain
\[\lambda = \frac{2\pi}{\beta} = \frac{2\pi}{\beta_0\sqrt{\epsilon_{r,eff}}} = \frac{\lambda_0}{\sqrt{\epsilon_{r,eff}}} \nonumber \]
where \(\lambda_0\) is the free-space wavelength \(c/f\). Similarly the phase velocity \(v_p\), can be estimated using the relationship \[v_p = \frac{\omega}{\beta} = \frac{c}{\sqrt{\epsilon_{r,eff}}} \nonumber \] i.e., the phase velocity in microstrip is slower than \(c\) by a factor of \(\sqrt{\epsilon_{r,eff}}\).
FR4 is a low-loss fiberglass epoxy dielectric that is commonly used to make printed circuit boards (see “Additional Reading” at the end of this section). FR4 circuit board material is commonly sold in a slab having thickness \(h\cong 1.575\) mm with \(\epsilon_r\cong 4.5\). Let us consider how we might implement a microstrip line having \(Z_0=50~\Omega\) using this material. Since \(h\) and \(\epsilon_r\) are fixed, the only parameter remaining to set \(Z_0\) is \(W\). A bit of experimentation with Equation \ref{m0082_eWheeler10} reveals that \(h/W\approx 1/2\) yields \(Z_0\approx 50~\Omega\) for \(\epsilon_r=4.5\). Thus, \(W\) should be about 3.15 mm. The effective relative permittivity is
\[\epsilon_{r,eff}\approx(4.5+1)/2 = 2.75 \nonumber \]
so the phase velocity for the wave guided by this line is about \(c/\sqrt{2.75}\); i.e., 60% of \(c\). Similarly, the wavelength of this wave is about 60% of the free space wavelength.


