11.7: Problems
- Page ID
- 19010
11.1. In the examples below, identify whether \(f\) is a function or a functional.
- A parabola is described by \(f(x) = x^2\).
- Given two forms of energy and a path \(y(t)\), \(f\) is the Lagrangian of the system \(\mathcal{L} \left( t, y, \frac{dy}{dt} \right)\).
- Given the magnitude of the velocity \(|\overrightarrow{v}(t)|\) of an object, \(f\) represents the distance that the object travels from time 0 to time 3600 seconds.
- Given the position \((x, y, z)\) in space, \(f(x, y, z)\) represents the distance from that point to the origin.
11.2. A system has the Lagrangian \(\mathcal{L} \left( t, y, \frac{dy}{dt} \right) = \left(\frac{dy}{dt}\right)^3 + e^{3y}\). Find an equation for the path \(y(t)\) that minimizes the action \(\int_{t_{1}}^{t_{2}} \mathcal{L}\left(t, y, \frac{d y}{d t}\right) d t\). (The result is nonlinear, so don't try to solve it.)
11.3. A system has Lagrangian \(\mathcal{L} \left( t, y, \frac{dy}{dt} \right) = \frac{1}{2}\left(\frac{dy}{dt}\right)^2 + \frac{1}{2} \cdot y^{-2}\). Find the corresponding equation of motion. (The result is nonlinear, so don't try to solve it.)
11.4. Figure 11.4.2 illustrates three possible paths for the mass spring system and their corresponding actions. The paths considered are:
\[x_{1}(t) = 2 t-1\nonumber \]
\[x_{2}(t) = 2 t^2-1\nonumber \]
\[x_{3}(t) =-\cos (\pi t)\nonumber \]
For each path, calculate the action using Equation 11.4.10 to verify the values shown in the figure. Assume a mass of \(m\) =1 kg and a spring constant of \(K = \pi^2 \frac{J}{m^2}\).
11.5. The figure shows a torsion spring. It can store potential energy \(\frac{1}{2} \mathbb{K} \theta^{2}\), and it can convert potential energy to kinetic energy\(\frac{1}{2} \mathbb{I}\left(\frac{d \theta}{d t}\right)^{2}\). In these expressions, \(\theta(t)\) is the magnitude of the angle the spring turns in radians, and \(\omega=\frac{d \theta}{d t}\) is the magnitude of the angular velocity in radians per second. \(\mathbb{K}\) is the torsion spring constant, and \(I\) is the (constant) moment of inertia.
(a) Find the Lagrangian.
(b) Use the Euler-Lagrange equation to find a differential equation describing \(\theta(t)\).
(c) Show that energy is conserved in this system by showing that \(\frac{dH}{dt} = 0\).
(d) Set up Hamilton's equations.

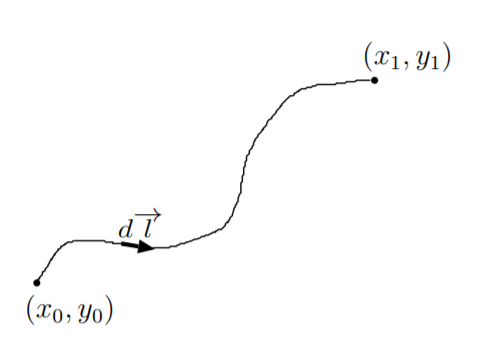
11.6. The purpose of this problem is to derive the shortest path \(y(x)\) between the points \((x_0, y_0)\) and \((x_1, y_1)\). Consider an arbitrary path between these points as shown in the figure. We can break the path into differential elements \(d\overrightarrow{l}=d x \hat{a}_{x}+d y \hat{a}_{y}\). The magnitude of each differential element is
\[|d \overrightarrow{l}|=\sqrt{(d x)^{2}+(d y)^{2}}=d x \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}.\nonumber \]
The distance between the points can be described by the action
\[\mathbb{S}=\int_{x_{0}}^{x_{1}} \sqrt{1+\left(\frac{d y}{d x}\right)^{2}} d x.\nonumber \]
To find the path \(y(x)\) that minimizes the action, we can solve the Euler-Lagrange equation, with \(\mathcal{L}=\sqrt{1+\left(\frac{d y}{d x}\right)^{2}}\) as the Lagrangian, for this shortest path \(y(x)\). This approach can be used because we want to minimize the integral of some functional \(\mathcal{L}\) even though this functional does not represent an energy difference [163, p. 33].
Set up the Euler-Lagrange equation, and solve it for the shortest path, \(y(x)\).
Hint 1: The answer to this problem is that the shortest path between two points is a straight line. Here, you will derive this result.
Hint 2: In the examples of this chapter, the Lagrangian had the form \(\mathcal{L} \left( t, y, \frac{dy}{dt} \right)\) with independent variable \(t\) and path \(y(t)\). Here, the Lagrangian has the form \(\mathcal{L} \left( x, y, \frac{dy}{dx} \right)\) where the independent variable is position \(x\), and the path is \(y(x)\).
Hint 3: If \(\frac{d} {dx} (something) = 0\), then you know that \((something)\) is constant.
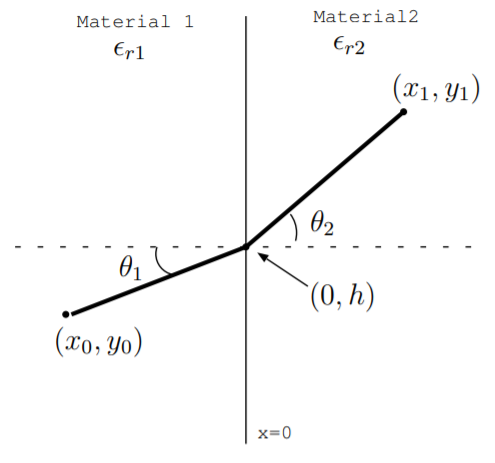
11.7. Light travels along the quickest path between two points. This idea is known as Fermat's principle. In a material with relative permittivity \(\epsilon_r\) and permeability \(\mu_0\), light travels at the constant speed \(\frac{c}{\sqrt{\epsilon_{r}}}\) where \(c\) is the speed of light in free space. In Prob. 11.6, we showed that the shortest path between two points is a straight line, so in a uniform material, light will travel along a straight line between two points. However, what if light travels across a junction between two materials? In this problem, we will answer this question and derive a famous result known as Snell's law.
Consider the figure below. Assume that a ray of light travels from \((x_0, y_0)\) to \((x_1, y_1)\) along the path which takes the shortest time. Material 1 has relative permittivity \(\epsilon_{r1}\), so the light travels in that material at a constant speed \(\frac{c}{\sqrt{\epsilon_{r1}}}\). Material 2 has relative permittivity \(\epsilon_{r2}\), so the light travels in that material at a constant speed \(\frac{c}{\sqrt{\epsilon_{r2}}}\). As we derived in the Prob. 11.6, the light travels along a straight line in material 1, and it travels along a straight line in material 2. However, the lines have different slopes as shown in the figure. Assume that the junction of the two materials occurs at \(x = 0\).
(a) Find an equation for the total time it takes the light to travel as a function of \(h\), the vertical distance at which the path crosses the \(y\) axis. Note that you are finding a function here, \(F(h)\), not a functional. You can use the fact that you know the light follows a straight line inside each material to find this function.
(b) The path followed by the light takes the minimum time, so the derivative \(\frac{dF}{dh} = 0\). Use this idea to find an equation for the unknown vertical height \(h\). Your answer can be written as a function of the known constants \(\epsilon_{r1}\), \(\epsilon_{r2}\), \(x_0\), \(y_0\), \(x_1\), \(y_1\), and \(c\). You do not need to solve for \(h\) here, but instead just evaluate the derivative and set it to zero.
(c) Use your result in part b above to derive Snell's law:
\[\sqrt{\epsilon_{r 1}} \sin \theta_{1}=\sqrt{\epsilon_{r 2}} \sin \theta_{2}.\nonumber \]
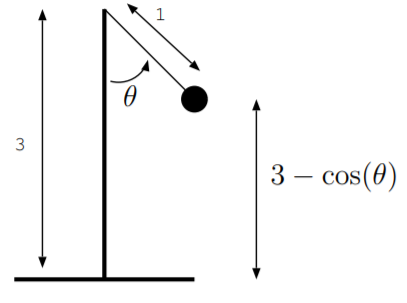
11.8. A pendulum converts kinetic energy to and from gravitational potential energy. As shown in the figure, a ball of mass m is hung by a string 1 m long. The pendulum is mounted on a base that is 3 m high. As shown in the figure, \(\theta(t)\) is the angle of the pendulum. The kinetic energy of the ball is given by \(E_{kinetic} = \frac{1}{2}m \left(\frac{d\theta}{dt}\right)^2\), and the gravitational potential energy is given by \(E_{p.e.} = mg (3 − \cos \theta)\). The quantity \(g\) is the gravitational constant, \(g = 9.8 \frac{m}{s^2}\).
(a) Find \(\mathcal{L}\), the Lagrangian of the system.
(b) Find \(H\), the Hamiltonian of the system.
(c) Set up the Euler-Lagrange equation, and use it to find the equation of motion for \(\theta(t)\), the angle of the pendulum as a function of time.
(d) Show that energy is conserved in this system by showing that \(\frac{dH}{dt} = 0\).
The equation of motion found in part c is nonlinear, so don't try to solve it. Interestingly, it does have a closed form solution [164, Ch. 6]. (This problem is a modified version of an example in reference [163].)
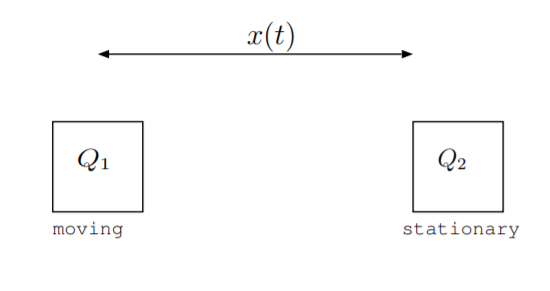
11.9. As shown in the figure, an object of charge \(Q_1\) and mass \(m\) moves near a stationary object with charge \(Q_2\). Assume the mass and the charges are constants, and assume the objects are surrounded by free space. The kinetic energy of the moving object is converted to or from energy stored in the electric field between the objects. The kinetic energy of the moving object is given by \(\frac{1}{2}m\left(\frac{dx}{dt}\right)^2\). The energy of the electric field is given by \(\frac{Q_1Q_2}{4\pi\epsilon_0x}\) where \(\epsilon_0\) is the permittivity of free space. The distance between the objects is given by \(x(t)\).
(a) Find the Lagrangian of the system.
(b) Find the generalized momentum.
(c) Find the generalized potential.
(d) Find the equation of motion for the path \(x(t)\) of the system. (Don't try to solve this nonlinear equation.)
(e) Find the total energy of the system.
(f) Show that energy is conserved in this system.