3.5: Telegrapher’s Equations

In this section, we derive the equations that govern the potential $v(z,t)$ and current $i(z,t)$ along a transmission line that is oriented along the $z$ axis. For this, we will employ the lumped-element model developed in Section 3.4.

To begin, we define voltages and currents as shown in Figure $\PageIndex{1}$.

Figure $\PageIndex{1}$: Lumped-element equivalent circuit transmission line model, annotated with sign conventions for potentials and currents. (© CC BY SA 3.0 Unported (modified))

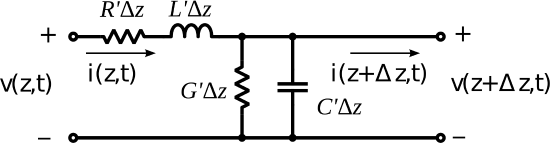
We assign the variables $v(z,t)$ and $i(z,t)$ to represent the potential and current on the left side of the segment, with reference polarity and direction as shown in the figure. Similarly we assign the variables $v(z+\Delta z,t)$ and $i(z+\Delta z,t)$ to represent the potential and current on the right side of the segment, again with reference polarity and direction as shown in the figure. Applying Kirchoff’s voltage law from the left port, through $R'\Delta z$ and $L'\Delta z$, and returning via the right port, we obtain:

$$\begin{gathered} v(z,t) - \left( R'\Delta z \right) i(z,t) - \left( L' \Delta z\right) \frac{\partial}{\partial t} i(z,t) \\ - v(z+\Delta z,t) = 0\end{gathered} \nonumber$$

Moving terms referring to current to the right side of the equation and then dividing through by $\Delta z$, we obtain

$$\begin{gathered} -\frac{v(z+\Delta z,t)-v(z,t)}{\Delta z} = \\ R'~i(z,t) + L'~\frac{\partial}{\partial t} i(z,t)\end{gathered} \nonumber$$

Then taking the limit as $\Delta z \rightarrow 0$:

$$\boxed{ -\frac{\partial}{\partial z} v(z,t) = R'~i(z,t) + L'~\frac{\partial}{\partial t} i(z,t) } \label{m0079_eTelegraphersEquation1}$$

Applying Kirchoff’s current law at the right port, we obtain:

$$\begin{gathered} i(z,t) - \left( G'\Delta z \right) v(z+\Delta z,t) - \left( C' \Delta z\right) \frac{\partial}{\partial t} v(z+\Delta z,t) \\ - i(z+\Delta z,t) = 0\end{gathered} \nonumber$$

Moving terms referring to potential to the right side of the equation and then dividing through by $\Delta z$, we obtain

$$\begin{gathered} -\frac{i(z+\Delta z,t)-i(z,t)}{\Delta z} = \\ G'~v(z+\Delta z,t) + C'~\frac{\partial}{\partial t} v(z+\Delta z,t)\end{gathered} \nonumber$$

Taking the limit as $\Delta z \rightarrow 0$:

$$\boxed{ -\frac{\partial}{\partial z} i(z,t) = G'~v(z,t) + C'~\frac{\partial}{\partial t} v(z,t) } \label{m0079_eTelegraphersEquation2}$$

Equations $\ref{m0079_eTelegraphersEquation1}$ and $\ref{m0079_eTelegraphersEquation2}$ are the telegrapher’s equations. These coupled (simultaneous) differential equations can be solved for $v(z,t)$ and $i(z,t)$ given $R'$, $G'$, $L'$, $C'$ and suitable boundary conditions.

The time-domain telegrapher’s equations are usually more than we need or want. If we are only interested in the response to a sinusoidal stimulus, then considerable simplification is possible using phasor representation.¹ First we define phasors $\widetilde{V}(z)$ and $\widetilde{I}(z)$ through the usual relationship:

$$v(z,t) = \mbox{Re}\left\{\widetilde{V}(z) ~ e^{j\omega t} \right\} \nonumber$$ $$i(z,t) = \mbox{Re}\left\{\widetilde{I}(z) ~ e^{j\omega t} \right\} \nonumber$$

Now we see:

$$\begin{split} \frac{\partial}{\partial z} v(z,t) & = \frac{\partial}{\partial z} \mbox{Re}\left\{\widetilde{V}(z) ~ e^{j\omega t} \right\} \nonumber \\ & = \mbox{Re}\left\{ \left[ \frac{\partial}{\partial z} \widetilde{V}(z) \right] ~ e^{j\omega t} \right\} \end{split} \nonumber$$

In other words, $\partial v(z,t)/\partial z$ expressed in phasor representation is simply $\partial \widetilde{V}(z)/\partial z$; and

$$\begin{split} \frac{\partial}{\partial t} i(z,t) & = \frac{\partial}{\partial t} \mbox{Re}\left\{\widetilde{I}(z) ~ e^{j\omega t} \right\} \nonumber \\ & = \mbox{Re}\left\{ \frac{\partial}{\partial t} \left[ \widetilde{I}(z) e^{j\omega t} \right] \right\} \nonumber \\ & = \mbox{Re}\left\{ \left[ j\omega \widetilde{I}(z) \right] e^{j\omega t} \right\} \end{split} \nonumber$$

In other words, $\partial i(z,t)/\partial t$ expressed in phasor representation is $j\omega \widetilde{I}(z)$. Therefore, Equation $\ref{m0079_eTelegraphersEquation1}$ expressed in phasor representation is:

$$\boxed{ -\frac{\partial}{\partial z} \widetilde{V}(z) = \left[ R' + j\omega L' \right]~\widetilde{I}(z) } \label{m0079_eTelegraphersEquation1p}$$

Following the same procedure, Equation $\ref{m0079_eTelegraphersEquation2}$ expressed in phasor representation is found to be:

$$\boxed{ -\frac{\partial}{\partial z} \widetilde{I}(z) = \left[ G' + j\omega C' \right]~\widetilde{V}(z) } \label{m0079_eTelegraphersEquation2p}$$

Equations $\ref{m0079_eTelegraphersEquation1p}$ and $\ref{m0079_eTelegraphersEquation2p}$ are the telegrapher’s equations in phasor representation.

The principal advantage of these equations over the time-domain versions is that we no longer need to contend with derivatives with respect to time – only derivatives with respect to distance remain. This considerably simplifies the equations.

---

1. For a refresher on phasor analysis, see Section 1.5.↩