4.2: The Series-Parallel Connection

Last updated
Save as PDF

Page ID: 25259

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Consider the circuit of Figure \(\PageIndex{1}\). This circuit is neither just a series circuit nor just a parallel circuit. If it was a series circuit then the current through all components would have to be same, that is, there would no nodes where the current could divide. This is clearly not the case as the current flowing through the capacitor can divide at node \(b\), with one portion flowing down through the resistor and the remainder through the inductor. On the other hand, if it was strictly parallel, then all of the components would have to exhibit the same voltage and therefore there would be only two connection points in the circuit. This is also not the case as there are three such points: \(a\), \(b\) and ground.

Figure \(\PageIndex{1}\): A simple series-parallel RLC circuit.

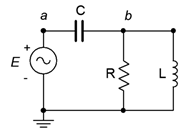
What is true for the circuit of Figure \(\PageIndex{1}\) is that the resistor and the inductor are in parallel. We know this because both components are attached to the same two nodes; \(b\) and ground, and must exhibit the same voltage, \(v_b\). As such, we can find the equivalent impedance of this pair and treat the result as a single value, let's call it \(Z_P\). In this newly simplified circuit, \(Z_P\) is in series with the capacitor and the source. We have simplified the original circuit into a series circuit and thus the series circuit analysis rules may be applied.