Appendix 1: Electric Circuits and Interconnection Laws
( \newcommand{\kernel}{\mathrm{null}\,}\)
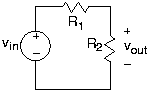
A circuit connects circuit elements together in a specific configuration designed to transform the source signal (originating from a voltage or current source) into another signal—the output—that corresponds to the current or voltage defined for a particular circuit element. A simple resistive circuit is shown in Figure A1.1 below. This circuit is the electrical embodiment of a system having its input provided by a source system producing vin(t).
 a)
a)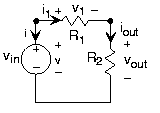 b)
b) c)
c)To understand what this circuit accomplishes, we want to determine the voltage across the resistor labeled by its value R2. Recasting this problem mathematically, we need to solve some set of equations so that we relate the output voltage vout to the source voltage. It would be simple—a little too simple at this point—if we could instantly write down the one equation that relates these two voltages. Until we have more knowledge about how circuits work, we must write a set of equations that allow us to find all the voltages and currents that can be defined for every circuit element. Because we have a three-element circuit, we have a total of six voltages and currents that must be either specified or determined. You can define the directions for positive current flow and positive voltage drop any way you like. Once the values for the voltages and currents are calculated, they may be positive or negative according to your definition. When two people define variables according to their individual preferences, the signs of their variables may not agree, but current flow and voltage drop values for each element will agree. Do recall in defining your voltage and current variables that the v-i relations for the elements presume that positive current flow is in the same direction as positive voltage drop. Once you define voltages and currents, we need six nonredundant equations to solve for the six unknown voltages and currents. By specifying the source, we have one; this amounts to providing the source's v-i relation. The v-i relations for the resistors give us two more. We are only halfway there; where do we get the other three equations we need?
What we need to solve every circuit problem are mathematical statements that express how the circuit elements are interconnected. Said another way, we need the laws that govern the electrical connection of circuit elements. First of all, the places where circuit elements attach to each other are called nodes. Two nodes are explicitly indicated in Figure A.1.1b; a third is at the bottom where the voltage source and resistor R2 are connected. Electrical engineers tend to draw circuit diagrams—schematics— in a rectilinear fashion. Thus the long line connecting the bottom of the voltage source with the bottom of the resistor is intended to make the diagram look pretty. This line simply means that the two elements are connected together. Kirchhoff's Laws, one for voltage and one for current, determine what a connection among circuit elements means. These laws are essential to analyzing this and any circuit. They are named for Gustav Kirchhoff, a nineteenth century German physicist.
Kirchhoff's Current Law
At every node, the sum of all currents entering or leaving a node must equal zero. What this law means physically is that charge cannot accumulate in a node; what goes in must come out. In the example Figure A1.1b above, we have a three-node circuit and thus have three KCL equations. (−i)−i1=0i1−i2=0i+i2=0
Note that the current entering a node is the negative of the current leaving the node.
Given any two of these KCL equations, we can find the other by adding or subtracting them. Thus, one of them is redundant and, in mathematical terms, we can discard any one of them. The convention is to discard the equation for the (unlabeled) node at the bottom of the circuit.
In writing KCL equations, you will find that in an n-node circuit, exactly one of them is always redundant. Can you sketch a proof of why this might be true? Hint: It has to do with the fact that charge won't accumulate in one place on its own.
- Solution
-
KCL says that the sum of currents entering or leaving a node must be zero. If we consider two nodes together as a "supernode", KCL applies as well to currents entering the combination. Since no currents enter an entire circuit, the sum of currents must be zero. If we had a two-node circuit, the KCL equation of one must be the negative of the other, we can combine all but one node in a circuit into a supernode; KCL for the supernode must be the negative of the remaining node's KCL equation. Consequently, specifying n−1 KCL equations always specifies the remaining one.
Kirchhoff's Voltage Law (KVL)
The voltage law says that the sum of voltages around every closed loop in the circuit must equal zero. A closed loop has the obvious definition: Starting at a node, trace a path through the circuit that returns you to the origin node. KVL expresses the fact that electric fields are conservative: The total work performed in moving a test charge around a closed path is zero. The KVL equation for our circuit is v1+v2−v=0
In writing KVL equations, we follow the convention that an element's voltage enters with a plus sign when traversing the closed path, we go from the positive to the negative of the voltage's definition.
For our example circuit, we have three v-i relations, two KCL equations, and one KVL equation for solving for the circuit's six voltages and currents. v-i:v=vinv1=R1i1vout=R2ioutKCL:(−i)−i1=0i1−iout=0KVL:−v+v1+vout=0
We have exactly the right number of equations! Eventually, we will discover shortcuts for solving circuit problems; for now, we want to eliminate all the variables but vout and determine how it depends on vin and on resistor values. The KVL equation can be rewritten as vin=v1+vout. Substituting into it the resistor's v-i relation, we have vin=R1i1+R2iout. Yes, we temporarily eliminate the quantity we seek. Though not obvious, it is the simplest way to solve the equations.
One of the KCL equations says i1=iout, which means that vin=R1iout+R2iout=(R1+R2)iout. Solving for the current in the output resistor, we have iout=vinR1+R2. We have now solved the circuit: we have expressed one voltage or current in terms of sources and circuit-element values. To find any other circuit quantities, we can back substitute this answer into our original equations or ones we developed along the way. Using the v-i relation for the output resistor, we obtain the quantity we seek. vout=R2R1+R2vin
Referring back to Figure A1.1, a circuit should serve some useful purpose. What kind of system does our circuit realize and, in terms of element values, what are the system's parameter(s)?
- Solution
-
The circuit serves as an amplifier having a gain of R2R1+R2.

