4.5: Catchment Volume
- Page ID
- 11939
Introduction
The catchment volume is calculated from the precipitation falling on the collection area with some loss due to the efficiency of the collection materials (and leaks). In addition, conversion factors are used to yield the desired units of volume. Typically, monthly catchment values are calculated based on monthly average precipitation data. The collection volume for any period of time is calculated using the following formula (mnemonic device Vrake):
\[V=R*a*k*e\]
Where:
- V = Volume of collection in \(\frac{gal}{time}\), \(\frac{m^3}{time}\), or \(\frac{liters}{time}\)
- Note that time is usually in months.
- Use this to help determine potential yield and tank size.
- R = Precipitation in \(\frac{inches}{time}\) or \(\frac{mm}{time}\)
- Collect this data or find it from existing climate data.
- A = Footprint of collection surface in \(ft^2\) or \(m^2\)
- This is the vertical projected area of the collection surface. For a rectangular house, use length times width.
- k = Needed conversion factors, such as 7.48 \(\frac{gal}{ft^3}\) or easier SI units
- Can also combine the 1 foot to 12 inches conversion for the precipitation data here.
- e = Efficiency of collection surface (which is unitless)
- 0.75 soil, 0.8 average, 0.95 metal
Imperial Units Example
Example \(\PageIndex{1}\)
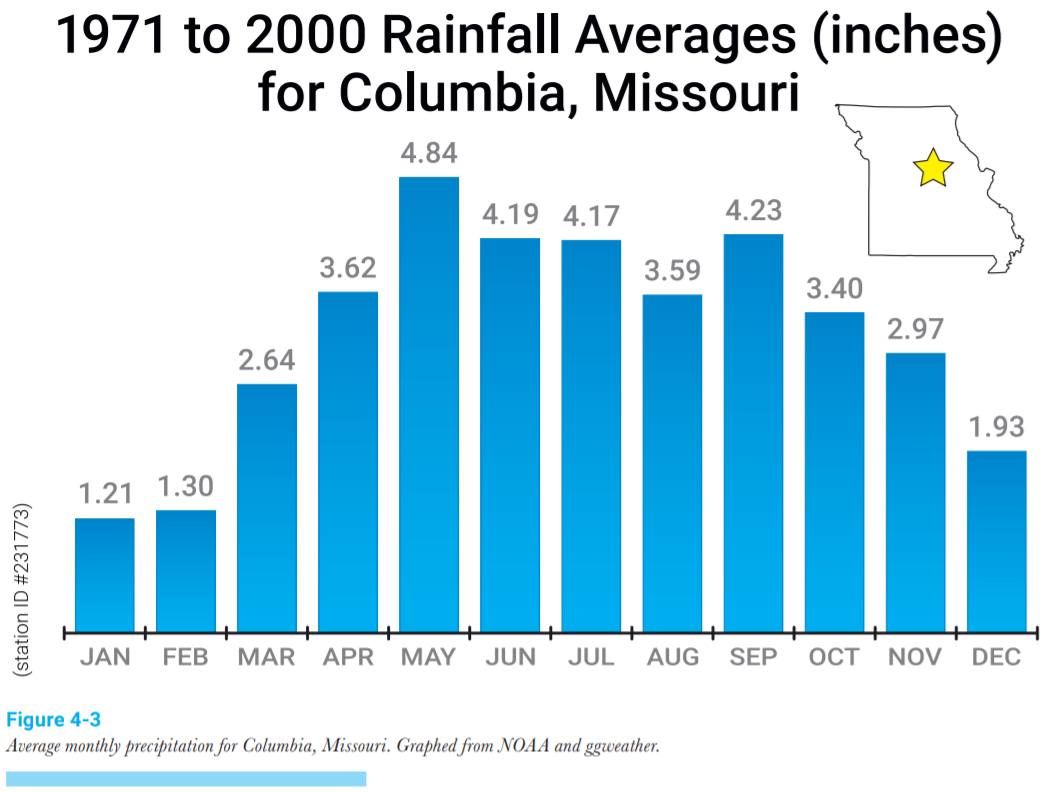
Calculate the collection potential (in gallons) for a 1,900 square foot single-story house, with a slanted shingle roof, in Columbia, Missouri for the month of March. The first step is finding the precipitation data for your location. For example, the table in Figure 4-3 shows the precipitation data for Columbia, Missouri.
Solution
Looking up the efficiency of the collection surface for a shingle roof yields an average of 0.8.
\[V=R*a*k*e\]
\[V(March)=\frac{2.64\;in}{March}*\frac{1\;ft}{12\;in}*1900\;ft*\frac{7.48\;gal}{ft^3}*0.8=2,500\;\frac{gal}{March}\]
Therefore, this 1,900 square foot house in Columbia, Missouri can collect a potential 2,500 gallons in the month of March.
SI Units Example
Example \(\PageIndex{2}\)
Calculate the collection potential (in liters) for a 100-square-meter house with concrete roof in Santo Domingo, Dominican Republic for the month of July.
Solution
Looking up the efficiency of the collection surface for a concrete roof yields an 0.9, and average rainfall for July is 145 mm:
\[V=R*a*k*e\]
\[V(July)=\frac{145\;mm}{July}*\frac{1\;m}{1000\;mm}*100\;m^2*\frac{1000\;liters}{m^3}*0.9=13,050\;\frac{liters}{July}\]
Therefore this 100-square-meter house in Santo Domingo, Dominican Republic can collect a potential 13,050 liters (3,447 gallons) in the month of July.
Rules of Thumb
The rule of thumb of 0.5 gallons of rainwater caught per inch of rain on each square foot of catchment is quite useful when doing quick calculations in the field.
\[Volume(gal)=0.5\frac{gal}{inches*ft^2}*rainfall(inches)*Area(ft^2)\]
The 0.5 gallon per square foot per inch of rain in the rule of thumb can be shown to assume about 0.8 roof efficiency, with the following equation:
\[1\;in*\frac{1\;ft}{12\;in}*1\;ft^2*7.48\frac{gal}{ft^3}*0.8=0.499\;gal\]
The calculation in SI units is much easier and more precise. It is the roof efficiency (e.g. 0.8) in liters for every mm of rain on every \(m^2\) of the roof.
\[Volume(liters)=roof\;efficiency*rainfall(mm)*Area(m^2)\]
This calculation is simple due to the convenience and synchronization of SI units, as shown below:
\[V=R*a*k*e\]
\[Volume=1\;mm*\frac{1\;m}{1000\;mm}*1\;m^2*1000\frac{l}{m^3}*0.8=0.8\;liters\]
Notice how the m to mm conversion cancels with the liters to \(m^3\) conversion


