4: Carrier Drift and Mobility
- Page ID
- 5956
Effective Mass and Statistical Considerations
When a free electron is perturbed by an electric field, it will be subject to forces that cause it to accelerate; it moves opposite the direction of the electric field, and would speed up with time. However, the situation in a crystal is different, because the electron is actually moving through a lattice of jiggling atoms that all exert electromagnetic forces. We cannot use the standard electron mass; we must use an effective mass for the electron in the crystal, a result of the periodic forces of the host atoms in the crystal1. The wonderful thing is that in the simple picture, we can view the electron as moving as though it were in a vacuum, but with this new effective mass that varies from material to material.
Another difference is that inside the crystal, a moving electron will not travel far before colliding with a host atom or impurity. These collisions randomize the electron’s motion; therefore, it is useful to use an average time, the relaxation time \(\tau\), which is based on the random thermal motion of the electrons. In fact, the scattering processes of the electron bouncing around causes it to lose energy, which is given off as heat. With the addition of an applied electric field, we also have a mean free path length \(\lambda\), or a net displacement on average for a given electron.
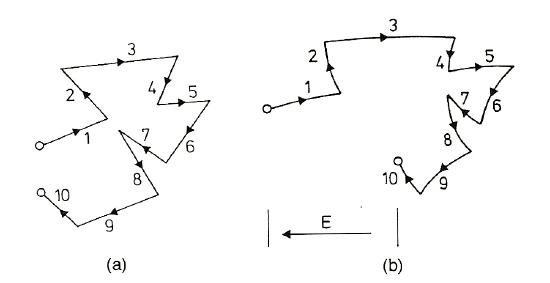
Above (Ref. 2): These pictures represent the drift of an electron as a result of thermal motion. In figure (a) where there is no electric field, the electron jumps around but ends up covering no net distance; in figure (b) where an electric field is present, the electron drifts opposite the direction of the field and has a net displacement (and therefore a drift velocity).
This means free charge carriers have a drift velocity, an average speed at which they travel through the material. The average drift velocity for a single electron is the same as the average of all drift velocities of all the electrons, and is given by the following equation:
\[ v_d = \dfrac{1}{2} a \tau = \dfrac{1}{2} \dfrac{q\tau}{m_c^*}E\]
where \(a\) is the average acceleration of the carrier, \(q\) is the charge of the carrier (including charge), \(m^*\) is the effective mass of the charge carrier, \(\tau\) is the carrier lifetime, and \(E\) is the electric field strength2.
Field Current and Mobility
The movement of charge carriers in an electric field results in an electric current. We will call the current resulting from drifting carriers our field current. The current density J, or the current flow of electrons per unit volume, is given by the following:
\[ J_n = nqv_d\]
\[J_n = nq\dfrac{1}{2} \dfrac{q\tau}{m^*}E\]
where n is the carrier concentration (per unit volume). Furthermore, we can get rid of the factor of 2 in this equation by averaging the lifetime τ over all carrier velocities1. Therefore, we can now define a quantity called mobility, in this case electron mobility. Carrier mobility is useful as it is the ratio of drift velocity to the electric field strength. Below we will give the mathematical definition and substitute mobility (given as μn) into the current density equation.
\[ \mu_n = \dfrac{\nu_d}{E} = \dfrac{q \tau}{m^*}\]
\[ J_n = nq\mu_n E\]
From these equations we can then obtain the conductivity of the material in terms of the mobility2:
\[ J_n = \sigma E\]
\[\sigma = nq \mu_n\]
The same conditions hold for hole mobility and conductivity, and therefore the total conductivity, which is directly inversely related to the resistivity (the material’s resistance to being conductive, so to speak), is given below:
\[ \sigma = \dfrac{1}{\rho} = \dfrac{J}{E} q \mu_e n + q \mu_h p\]
where \(ρ\) is the resistivity, \(n\) and \(p\) are the concentrations of electrons and holes respectively, and \(μ_e\) and \(μ_h\) are the electron and hole mobilities respectively.
We see that conductivity in a material is directly related to the mobility, which depends on the density of dopants, temperature, and electric field strength. Thus, as mobility decreases conductivity decreases. As materials become more heavily doped, mobility decreases because dopant atoms are very effective scatterers, and therefore decrease the average time between collisions. Similarly, as temperature increases, mobility decreases, however this effect becomes insignificant in heavily doped materials. As electric field increases, the drift velocities of carriers will eventually become comparable to the random thermal velocities. Therefore, high field strength decreases mobility; semiconductors in this way differ from conductors, which so easily generate current that only a low field strength occurs during current flow2. It is worth noting that less specialized impurities and crystal defects in the semiconductor material will also decrease the mobility, because of the scattering effects mentioned above.
References
- Green, Martin A. Solar Cells: Operating Principles, Technology, and System Applications. Englewood Cliffs: Prentice-Hall, Inc., 1982. Full book ordering information at www.pv.unsw.edu.au.
- Goetzberger, Adolf et.al. Crystalline Silicon Solar Cells. Chichester: John Wiley & Sons Ltd., 1998.

